Compound Interest – Explanation & Examples

Compound interest can be stated as the addition of interest on interest. Therefore, compound interest can help the investors in faster growth of their investments. It is the interest that is added to the principal amount/sum of loans or deposits and the accumulated interests. Therefore, it helps in the exponential growth of one’s investment.

Compound interest is the interest added on both the principal loan/deposit and the accumulated interest from the previous periods.

You should refresh the following concepts to understand the material discussed on this topic.

1. Percentage.
2. Simple Interest.

What is Compound Interest

Compound interest is a method used for the calculation of interest on a principal loan or deposit. Investors use the compound interest method worldwide to carry out interest-related calculations for their financial transactions.

Investors are interested more in compound interest as compared to simple interest.  In the case of simple interest, no accumulated value is added to the principal amount.  For example, a principal amount of 1000 dollars is invested for 3 years with an annual interest rate of 10%. The simple interest for all the 3 periods will be 100, 100, and 100 dollars, while the compound interest for the 3 periods will be 100, 110, and 121 dollars.

Compound Interest Definition:

Compound interest is the interest earned on the deposited principal amount plus the previously accumulated interest for the given period.

How to Calculate Compound Interest

To understand the calculation of compound interest, first, you should understand the concept of simple interest. If you are depositing money in a bank for some period, the bank pays you interest on your deposited amount. For example, you have deposited 200 dollars for a period of 3 years with an interest rate of 10 %.  If the bank is using a simple interest rate, then the total interest at the end of 3 years will be

$I = P \times R \times T$

$I = 200 \times 10 \% \times 3$

$I = (200 \times 10 \times 3)/ 100$

$I = 60$ dollars

Alternative Solution

$Simple\hspace{1mm} Interest \hspace{1mm} at\hspace{1mm} end\hspace{1mm} of\hspace{1mm} first\hspace{1mm} year\hspace{1mm} = 200 \times 10 \% \times 1 = 20 $ dollars

$Simple\hspace{1mm} Interest\hspace{1mm} at\hspace{1mm} end \hspace{1mm}of\hspace{1mm} second \hspace{1mm}year\hspace{1mm} = 200 \times 10 \% \times 1 = 20 $ dollars

$Simple\hspace{1mm} Interest\hspace{1mm} at\hspace{1mm} end\hspace{1mm} of\hspace{1mm} third\hspace{1mm} year = 200 \times 10 \% \times 1 = 20 $ dollars

$Total\hspace{1mm} simple\hspace{1mm} interest = 20\hspace{1mm} +\hspace{1mm}20\hspace{1mm} +\hspace{1mm}20 = 60 $ dollars

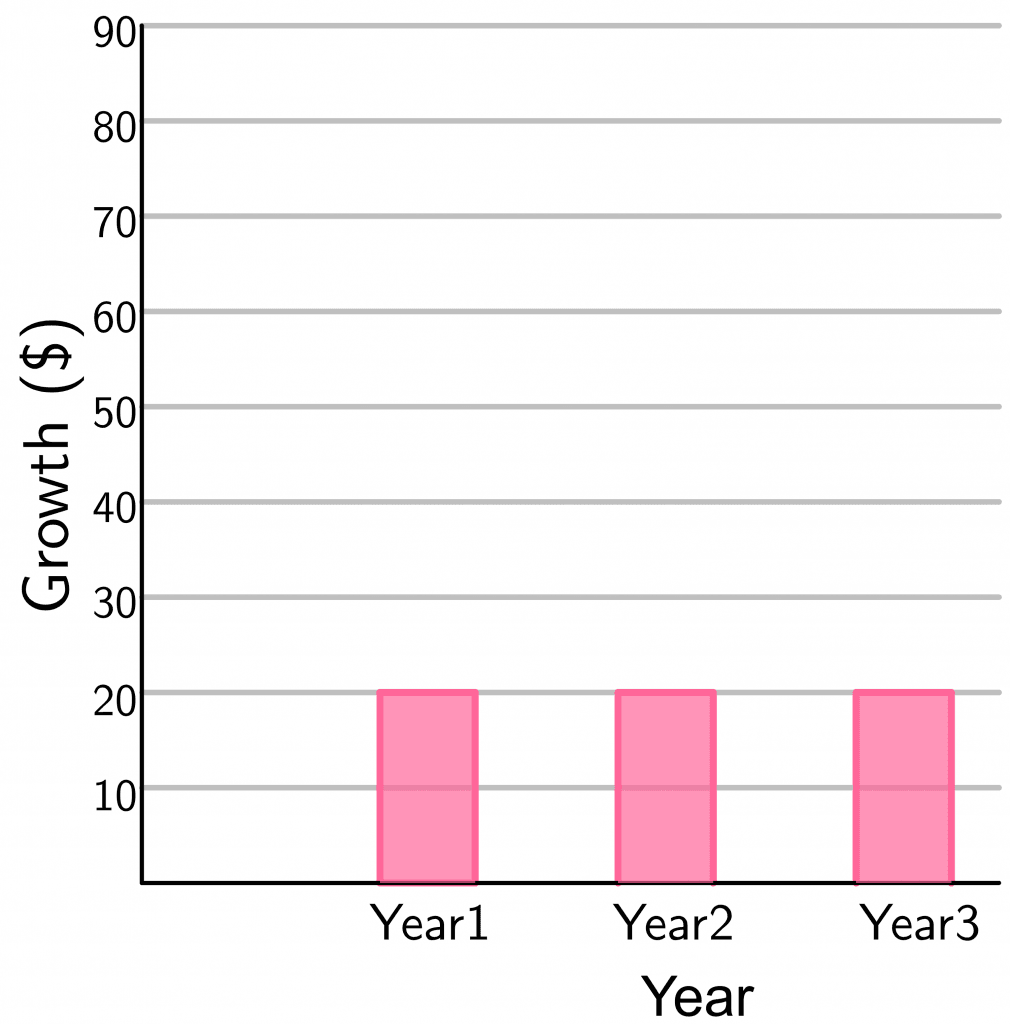
This amount is added to the principal amount, and you get the new principal amount at the end of the third year, i.e., $200\hspace{1mm} +\hspace{1mm} 60 = 260$ dollars.

If the bank is using the compound interest method, then the interest at the end of year one is

                                    $Interest\hspace{1mm} at\hspace{1mm} end\hspace{1mm} of\hspace{1mm} year\hspace{1mm} one  = 200 \times 10\% = 20$.

                                    $New\hspace{1mm} Principal\hspace{1mm} amount = 200\hspace{1mm} +\hspace{1mm}20 = 220$.

                        $Interest\hspace{1mm} at\hspace{1mm} the\hspace{1mm} end\hspace{1mm} of\hspace{1mm} year\hspace{1mm} 2 = 220 \times 10 \% = 22$.

                        $Principal\hspace{1mm} amount\hspace{1mm} at\hspace{1mm} the\hspace{1mm} end \hspace{1mm}of \hspace{1mm}year\hspace{1mm} 2 = 220 +22 = 242$.

                        $Interest\hspace{1mm} at\hspace{1mm} the end\hspace{1mm} of\hspace{1mm} year\hspace{1mm} 3 = 242 \times 10\% = 24.2$.

                        $Principal\hspace{1mm} amount\hspace{1mm} at\hspace{1mm} the\hspace{1mm} end \hspace{1mm}of \hspace{1mm}year\hspace{1mm} 3 = 242 + 24.2 = 266.2$ dollars.

Alternative Solution

$Cumulative\hspace{1mm} C. I = 20\hspace{1mm} +22\hspace{1mm} + \hspace{1mm}24.2 = 66.2 $

$Final\hspace{1mm} principal\hspace{1mm} amount = 200 \hspace{1mm}+\hspace{1mm} 66.2 = 266.2$ dollars.

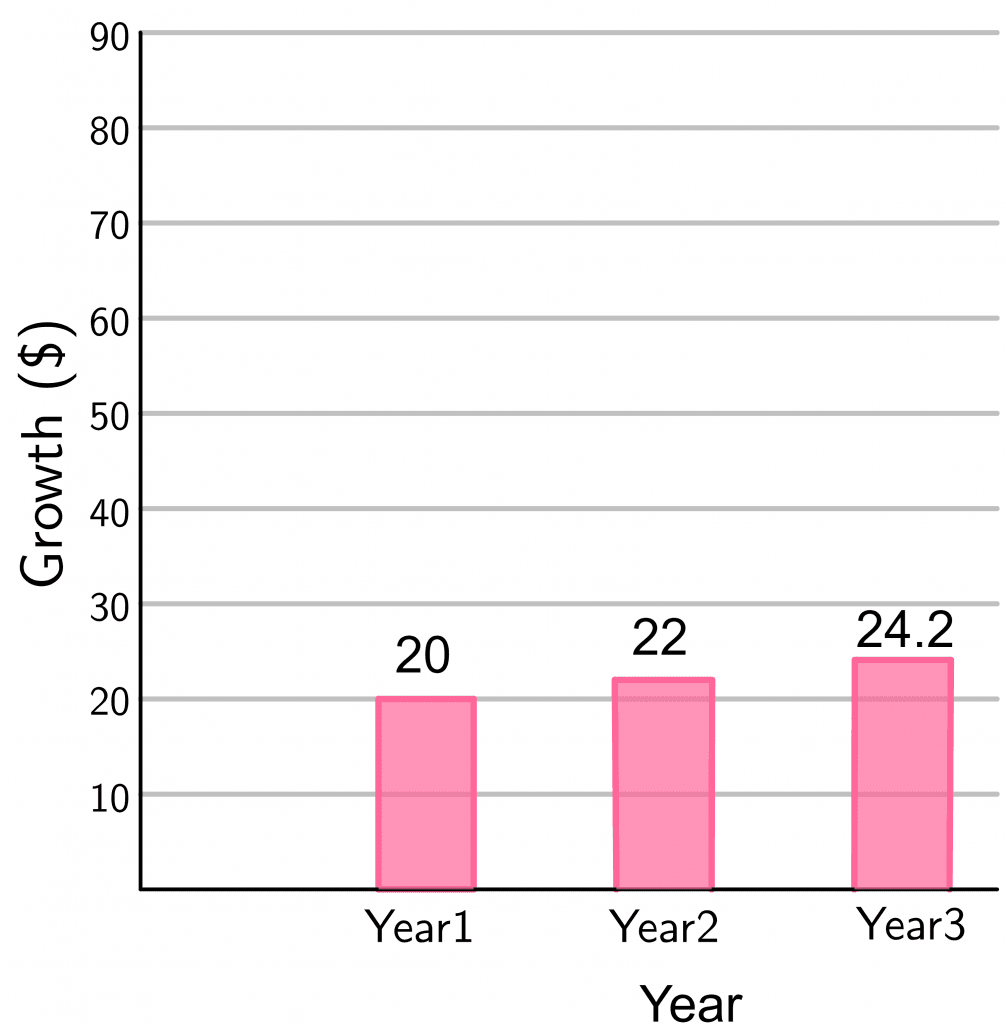
As we can see, the principal amount at the end of the third year with compounded interest is more significant than that of the simple interest; therefore, investors prefer this accumulated interest method while depositing. Similarly, banks also prefer this method while loaning out money.

In short, compound interest can be stated as:

Compound Interest = Interest on Principal loan or deposit + Accumulated Interest over a given interval of time.

Compound Interest Formula:

The final amount to be calculated using compound interest can be written using the formula given below.

$\mathbf{ A = P (1+\frac{r}{n})^{nt}}$

Here,

A = the final amount at the end of the given time interval.

P = Initial or starting principal amount

r = rate of interest

t = total time period

n = number of times the interest is compounded. (It can be annually, monthly, Bi-monthly, etc.).

The above formula is used to calculate the final amount at the end of the given time period. If you only want to calculate the compound interest of the given period, then you have to subtract the principal amount from the given formula.

$\mathbf{ C.I = P (1+\frac{r}{n})^{nt} – P}$

Compound Interest Formula for Different Time Intervals:

Compound interest for a given principal amount can be calculated for different time intervals. The formulas for these calculations are given below.

•  Compound Interest Formula for Semi-Annual Time Period

The basic method for the calculation of annual compound interest is discussed above. What if interest is to be calculated for a semi-annual interval? The semi-Annual period consists of six months; in that case, the principal amount is compounded 2 times or twice a year, and the interest rate of that period is also divided by 2. We can write the formula for the calculation of compound interest for the semi-annual time period as.

$\mathbf{Semi-Annual\hspace{1mm} C.I = P (1+\frac{r/2}{100})^{2t} – P}$

Here,

C.I = Compound Interest.

P = Initial or starting principal amount

r = rate of interest given in a fraction

t = total time period

n = number of times the interest is compounded. In this case $n = 2$.

If you want to calculate the principal amount compounded semi-annually, You will write the formula as.

$\mathbf{Semi-Annual\hspace{1mm} P.A = P (1+\frac{r/2}{100})^{2t}}$

• Compound Interest Formula for Quarterly Time Period

When the interest is compounded quarterly, then the initial principal amount is compounded four times a year after every 3 months. So, the value of ‘n’ in this case will be 4.  We can give the compound interest calculation for quarterly intervals as.

$\mathbf{Quarterly\hspace{1mm} C.I = P (1+\frac{r/4}{100})^{4t} – P}$

The calculation of ‘n’ value is essential for the successful implementation of the compound interest method. A year is taken as a base for the calculation of all other time intervals. In this case, we have divided the year quarterly, hence the value of n = 4. We can give the formula for calculation of principal amount for the quarterly time period as.

$\mathbf{Quarterly\hspace{1mm} P.A = P (1+\frac{r/4}{100})^{4t}}$

•  Compound Interest Formula for Monthly Time Interval

If the principal amount is compounded every month, then the value of n will be 12. Therefore, We can give the compound interest formula for the monthly time period as.

$\mathbf{Monthly\hspace{1mm} C.I = P (1+\frac{r/12}{100})^{12t} – P}$

Similarly, the principal amount for the said period can be calculated using the formula given below.

$\mathbf{Monthly\hspace{1mm} P.A = P (1+\frac{r/12}{100})^{12t}}$

• Compound Interest Formula for Bi-Monthly or Semi-Monthly Time Interval

The term bi-monthly means twice a month, so we use the term bi-monthly or semi-monthly for a principal amount that is to be compounded twice a month.

For example, a year has 12 months in it, and if we divide a month into two parts, then the value of ‘n’ in this case will be $n = 12 \times 2 = 24$. So, the compound interest formula for a principal amount that is compounded bi-monthly can be given as.

$\mathbf{Bi – Monthly\hspace{1mm} C.I = P (1+\frac{r/24}{100})^{24t} – P}$

Similarly, We can calculate the principal amount for the said period through the given formula.

$\mathbf{Bi – Monthly\hspace{1mm} P.A = P (1+\frac{r/24}{100})^{24t}}$

• Compound Interest Formula for Daily basis

If the principal amount is compounded daily, the value of ‘n’ is taken as 365. We know that a year has 365 days, so the formula for calculation of compound interest, if the principal amount is compounded daily, is given as.

$\mathbf{Daily\hspace{1mm} C.I = P (1+\frac{r/365}{100})^{365t} – P}$

Similarly, the principal amount for the said period can be calculated through the given formula.

$\mathbf{Daily\hspace{1mm} P.A = P (1+\frac{r/365}{100})^{365t}}$

Compound Interest and Calculations of Future Values:

Compound interest has many applications and is used to calculate future values, annuities, and perpetuities. One of the important applications of compound interest is the calculation of future values. The formula for the calculation of future values is derived from the compound interest formula. The future value of all the loans/investments with compound interest can be calculated using the future value formula. Any person taking a loan, or investing an amount, will consider/calculate the future financial implications of the said loan or investment. All of the commercial, financial structure deals with interest rate and the majority of the interest rate structure follows the compound interest method.

Let’s say you have invested 2000 dollars at an interest rate of 5 % for a period of 3 years. You are required to calculate the future value of an investment using simple and compound interest.

For the simple Interest rate

$I = P\times R \times T$

$I = 2000 \times 5 \% \times 3$

$I = (200 \times 10 \times 3)/100$

$I = 300$ dollars.

Final value can be calculated as 2000 + 300 = 2300 dollars.

We can do the same calculation in a swift manner using the future value formula.

$F.V = P (1+ r \times t)$

Here,

$P = 2000$ dollars

$r = 5\%$

$t = 3$

$F.V = 2000 (1+ 0.05 \times 3)$

$F.V = 2300$ dollars.

The final value calculated in both methods is the same. That is why both of these formulas go hand in hand.

Similarly, if we want to calculate the final value using compound interest then the calculations would be

Interest at end of year one $ = 2000 \times 0.05 = 100$.

New Principal amount $= 2000 +100 = 2100$.

Interest at the end of year 2 $= 2100 \times 0.05 = 105$.

Principal amount at the end of year 2 $= 2100 +105 = 2205$.

Interest at the end of year 3 $= 2205 \times 0.05 = 110.25$.

Principal amount at the end of year 3 $= 2205 + 110.25 = 2315.25$. Dollars

Future value formula for investment/loan involving compound interest can be given as.

$F.V = P (1+ r)^t$    

$F.V = 2000 (1 + 0.05)^3$

$F.V = 2000 (1.05)^3$

$F.V = 2000 \times 1.1576 = 2315.25$ dollars.

The final value is the same using both methods.

Advanced Problems related to Compound Interest:

So far, we have discussed compound interest calculation for a single principal amount invested or loaned for a given period. A question arises: How can I calculate the future value if I want to make multiple investments during a given period?  The answer to that question lies in the previous topic we discussed regarding future values, as we will use it to calculate annuities or future values regarding complex compound interest problems.

Let’s say Harry is investing an amount of 1000 Dollars on a semi-annual basis into his savings account at a bank with an annual interest rate of 12%; the interest is compounded quarterly. Calculations for the final amount after the period of 12 months can be done using the annuity future value formula.

$F. V. A = P\times\left ( \frac{Future. Value -1 }{r/n} \right )$

$F. V. A = P\times\left ( \frac{(1+r/n)^{nt} -1 }{r/n} \right )$

Here,

Principal Amount P = 1000 but it invested on semi – annual basis, hence

$P = \frac {1000}{2} = 500$

$r = 12 \%$

$n = 4$

$\frac{r}{n} = \frac{12}{4}= 3\% = 0.03$

$t = 1$

$F. V. A = 500\times\left ( \frac{(1+ 0.03)^{4} -1 }{0.03} \right)$

$F. V. A = 500\times\left ( \frac{(1.03)^{4} -1 }{0.03} \right)$

$F. V. A = 500\times\left ( \frac{1.1255 -1 }{0.03} \right )$

$F. V. A = 500\times 4.184 = 2091.81$ Dollars.

Example 1:  Calculate the final amount by using simple and compound interest methods for the given data.

Principal amount $= 400$

Time Period$ = 2$ Years

Interest Rate $= 10\%$

Solution:

Simple interest can be calculated by formula $I = P \times R \times T$

$ I = 400 \times 10\% \times 2$

$ I = 400 \times 10 \times 2 /100$

$ I = 8000 / 100 $

$ I = 80 $

$ Final Amount = 400+80 = 480 $ dollars

For calculation of compound interest, we know the principle value is 400

P= 400

Interest for first year $= 400 \times 10\% = 40$

New Principal amount $= 400 + 40 = 440$

Interest for second year $= 440 \times 10\% = 44$

Principal amount at end of second year $= 440 + 44 = 484$

Compound Interest $= 40 + 44 = 84$

Final Amount = Principal Amount + Accumulated Interest

Final Amount $= 400 + 84 = 484$ dollars

Example 2:  Harris has taken a loan of 5000 dollars from the bank. Bank will charge an interest rate of 10 % per annum, compounded monthly for a period of 5 years. You are required to help Harris calculate the final Amount he has to pay back to the bank.

Solution:

$P = 5000$

$r = 10\%$

$n = 4$

$t = 5$

$A = P (1+\frac{r/12}{100})^{12t}$

$A = 5000 (1+\frac{10/12}{100})^{12\times5}$

$A = 5000 (1+ 0.0083)^{60}$

$A = 5000 (1.083)^{60}$

$A = 5000 \times 1.642$

$A = 8210$ dollars.

Example 3: Annie lends a loan of 10,000 dollars to Claire at an interest rate of 10%, compounded bi-monthly for a period of 4 years. You are required to help Annie calculate the final amount she will receive at the end of the 4^th year.

Solution:

$P = 10,000$

$r = 10\%$

$n = 24$

$t = 4$

$A = P (1+\frac{r/24}{100})^{24t}$

$A = 10,000 (1+\frac{10/24}{100})^{24\times4}$

$A = 10,000 (1+ 0.00416)^{96}$

$A = 10,000 (1.0042)^{96}$

$A = 10,000 \times 1.495$

$A = 14950$ dollars.

Example 4: ABC International Ltd makes an investment of 1 million dollars for a period of 3 years. Find the final value of the asset at the end of 3^rd year if the investment earns the return of 5 % compounded semi-annually.

Solution:

$P = 1000000$

$r = 5\%$

$n = 2$

$t = 3$

$A = P (1+\frac{r/2}{100})^{2t}$

$A = 1000000 (1+\frac{5/2}{100})^{2\times3}$

$A = 1000000 (1+ 0.025)^{6}$

$A = 1000000 (1.025)^{6}$

$A = 1000000 \times 1.1596$

$A = 1159600$ dollars.

Example 5: Henry wants to invest his 1 million Dollars in a commercial bank. Given below is the list of banks with their interest rate details. You are required to help Henry in the selection of the best investment option.

• Bank A is offering a 10 % interest rate, compounded semi-annually for a period of 3 years.
• Bank B is offering a 5 % interest rate, compounded monthly for a period of 2 years.
• Bank C is offering a 10 % interest rate, compounded quarterly for a period of 3 years.

Solution:

From the above calculations, it is clear that Mr. Henry should invest his amount in Bank C.

Note: Compound interest is calculated by subtracting the principal amount from the answer of the formula. For example, in the case of bank A the compound interest is finally calculated $C.I=1340000 – 1000000 $. Here $1340000$ is the final principal amount. So,  If we do not subtract the initial principal amount from the final answer of Compound interest that will give us the principal amount. For Bank A, B, and C that value is 1340000, 1104941.33, and 134488.824 Dollars respectively