JUMP TO TOPIC
Constant of Proportionality – Explanation & Examples
Constant of Proportionality is a number that relates two variables. The two variables can be directly or inversely proportional to each other. When the two variables are directly proportional to each other, the other variable increases as well.
When the two variables are inversely proportional to each other, the other will decrease if one variable increases. For example, the relation between two variables, $x$ and $y$, when they are directly proportional to each other is shown as $y = kx$ and when they are inversely proportional, is shown as $y =\frac{k}{x}$. Here “k” is the constant of proportionality.
Constant of Proportionality is a constant number denoted by “k,” which is either equal to the ratio of two quantities if they are directly proportional or product of two quantities if they are inversely proportional.
You should refresh the following concepts to understand the material discussed on this topic.
- Basic Arithmetic.
- Graphs
What is the Constant of Proportionality
Constant of proportionality is the constant that is generated when two variables form a direct or inverse relationship. The value of the constant of proportionality depends on the type of relationship. The value of “k” will always remain constant irrespective of the type of relationship between two variables. The constant of proportionality is also known as the coefficient of proportionality. We have two types of proportions or variations.
Directly Proportional: If you give two variables, “y” and “x,” then “y” will be directly proportional to “x” if an increase in the value of the variable “x” causes a proportional increase in the value of “y.” You can show the direct relationship between two variables as.
$y \,\, \alpha \,\,x$
$ y = kx $
For example, you want to buy 5 chocolates of the same brand but have not decided which brand of chocolate you want to buy. Let’s say the available brands at the shop are Mars, Cadbury, and Kitkat. The variable “x” is the cost of one chocolate while “k” is the constant of proportionality, and it will always be equal to 5, as you have decided to purchase 5 chocolates. In contrast, variable “y” will be the total cost of the 5 chocolates. Let us assume the prices of the chocolates are
$Mars = 8\hspace{1mm}dollars$
$Cadbury = 2 \hspace{1mm}dollars$
$Kitkat = 6 \hspace{1mm}dollars$
As we can see, the variable “x” can be equal to 5, 2, or 6 depending on which brand you want to buy. The value of “y” is directly proportional to the value of “x,” if you buy the expensive chocolate, the overall cost will also increase, and it will be greater than the rest of the two brands. You can calculate the value of “y” by using the equation $ y = 5x $
X | K | Y |
| $8$ | $5$ | $8\times 5 =40$ |
| $2$ | $5$ | $2\times 5 =10$ |
| $6$ | $5$ | $6\times 5 =30$ |
Inversely Proportional: The two given variables “y” and “x” will be inversely proportional to each other if an increase in the value of the variable “x” causes a decrease in the value of “y.” You can show this inverse relationship between two variables as.
$y \,\, \alpha \,\, \dfrac{1}{x}$
$ y = \dfrac{k}{x} $
Let us take the example of Mr. Steve, who is driving a car to travel from destination “A” to destination “B.” The total distance between “A” and “B” is 500KM. The maximum speed limit on the highway is 120 KM/hr. In this example, the speed at which the car is moving is variable “x” while “k” is the total distance between destination “A” and “B” as it is constant. The variable “y” is the time in “hours” to reach the final destination. Mr. Steve can drive at any speed below 120KM/hr. Let us calculate the time to go from destination A to B if the car was moving at a) 100KM/hr b) 110/KM/hr c) 90Km/hr.
| X | K | Y |
| $100$ | $500$ | $\dfrac{500}{100} =5hrs$ |
| $110$ | $500$ | $\dfrac{500}{110} =4.5hrs$ |
| $90$ | $500$ | $\dfrac{500}{100} =5.6hrs$ |
As we can see in the above table, if the car moves at a higher speed, it will take less time to reach the destination. When the value of variable “x” increases, the value of variable “y” decreases.
How to Find the Constant of Proportionality
We have developed our knowledge related to both types of proportions. The constant of proportion is easy to find once you have analyzed the relationship between the two variables.
Let us first take the previous examples of chocolates which we discussed earlier. In that example, we pre-determined the value of “k” to be equal to 5. Let us change the values of variables and draw a graph. Suppose we have 5 chocolates with prices 2,4,6,8 and 10 dollars respectively. The value of “x” increases by steps of 2 while the value of “k” remains constant at 5, and by multiplying “x” by “k” we get the values of “y.” If we plot the graph, we can observe that a straight line is formed, which describes a direct relationship between the two variables.
The constant of proportionality “k” is the slope of the line plotted by using the values of the two variables. In the graph below, the slope is marked as the constant of proportionality.
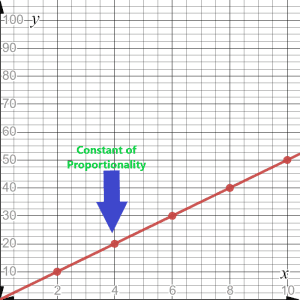
The above example explained the concept of constant of proportionality using a graph, but the value of “k” was pre-determined by us. So let us take an example where we have to find the value of “k.”
Example 1: The table below contains the values of the two variables, “x” and “y.” Determine the type of relationship between the two variables. Also, calculate the value of the constant of proportionality?
X | Y |
| $1$ | $3$ |
| $2$ | $6$ |
| $3$ | $9$ |
| $4$ | $12$ |
| $5$ | $15$ |
Solution:
The first step is to determine the type of relationship between the two variables.
Let us first try to develop an inverse relationship between these two variables. We know the inverse relation is shown as.
$ y = \dfrac{k}{x} $
$ k = y. x $
| X | Y | K |
| $1$ | $3$ | $k = 3\times 1 = 3$ |
| $2$ | $6$ | $k = 2\times 6 = 12$ |
| $3$ | $9$ | $k = 3\times 9 = 27$ |
| $4$ | $12$ | $k = 4\times 12 = 48$ |
| $5$ | $15$ | $k = 5\times 15 = 75$ |
As we can see the value of “k” is not constant, hence the two variables are not inversely proportional to each other.
Next, we will see if they have a direct relation between them. We know the formula for direct relation is given as.
$ y = kx $
| X | Y | K |
| $1$ | $3$ | $k = \dfrac{3}{1} = 3$ |
| $2$ | $6$ | $k = \dfrac{6}{2} = 3$ |
| $3$ | $9$ | $k = \dfrac{9}{3} = 3$ |
| $4$ | $12$ | $k = \dfrac{12}{4} = 3$ |
| $5$ | $15$ | $k = \dfrac{15}{5} = 3$ |
We can see that the value of “k” remains constant; hence both the variables are directly proportional to each other. You can draw the slope of the given relationship as.
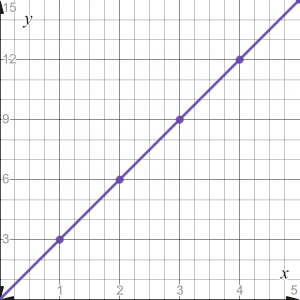
Example 2: The table below contains the values of the two variables, “x” and “y.” Determine the type of relationship between the two variables. Also, calculate the value of the constant of proportionality?
| X | Y |
| $10$ | $\dfrac{1}{5}$ |
| $8$ | $\dfrac{1}{4}$ |
| $6$ | $\dfrac{1}{3}$ |
| $4$ | $\dfrac{1}{2}$ |
| $2$ | $1$ |
Solution:
Let us determine the type of relationship between the two variables.
We know the inverse relation formula is given as.
$ y = \dfrac{k}{x} $
$ k = y. x $
| X | Y | K |
| $10$ | $\dfrac{1}{5}$ | $k = \dfrac{10}{5} = 2$ |
| $8$ | $\dfrac{1}{4}$ | $k = \dfrac{8}{4} = 2$ |
| $6$ | $\dfrac{1}{3}$ | $k = \dfrac{6}{3} = 2$ |
| $4$ | $\dfrac{1}{2}$ | $k = \dfrac{4}{2} = 2$ |
| $2$ | $1$ | $k = \dfrac{2}{1} = 2$ |
We can see from the table that the value of “k” remains constant; hence both the variables are inversely proportional. You can draw the slope of the given relationship as.
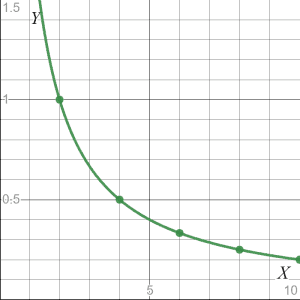
Two variables can either be directly or inversely proportional to each other. Both relations cannot exist simultaneously. In this example, as they are inversely proportional to each other, they cannot be directly proportional.
Constant of Proportionality Definition:
Constant of proportionality is the ratio between two variables that are directly proportional to each other, and it is generally represented as
$\mathbf{k =\dfrac{y}{x}}$
Example 3: The table below contains the values of the two variables, “x” and “y.” Determine whether a relationship exists between these two variables. If yes, then find the type of relationship between the two variables. Also, calculate the value of the constant of proportionality.
| X | Y |
| $3$ | $6$ |
| $5$ | $10$ |
| $7$ | $15$ |
| $9$ | $18$ |
| $11$ | $33$ |
Solution:
The relationship between the two variables can either be direct or inverse.
Let us first try to develop a direct relationship between given variables. We know the direct relation formula is given as.
$ y = kx $
| X | Y | K |
| $3$ | $3$ | $k = \dfrac{3}{3} = 1$ |
| $5$ | $6$ | $k = \dfrac{6}{5} = 1.2$ |
| $7$ | $9$ | $k = \dfrac{9}{7} = 1.28$ |
| $9$ | $12$ | $k = \dfrac{12}{9} = 1.33$ |
| $11$ | $15$ | $k = \dfrac{15}{11} = 1.36$ |
As we can see the value of “k” is not constant, hence the two variables are not directly proportional to each other.
Next, let us try to develop an inverse relation between them. We know the formula for inverse relation is given as.
$ y = \frac{k}{x} $
$ k = y. x $
| X | Y | K |
| $3$ | $3$ | $k = 3\times 3 = 9$ |
| $5$ | $6$ | $k = 6\times 5 = 30$ |
| $7$ | $9$ | $k = 9\times 7 = 63$ |
| $9$ | $12$ | $k = 12\times 9 = 108$ |
| $11$ | $15$ | $k = 15\times 11 = 165$ |
So, the variables do not form a direct or inverse relationship with each other as the value of “k” does not remain constant in both cases.
Example 4: If 3 men complete a work in 10 hours. How much time will be taken by 6 men to do the same task?
Solution:
As the number of men increases, the time taken to do the task decreases. So it is clear that these two variables have an inverse relationship. So let us represent the men by variable “X” and working hours by variable “Y.”
X1= 3, Y1= 10, X2 = 6 and Y2 =?
We know the formula for inverse relationship is given as
$ Y1 = \dfrac{k}{X1} $
$ k = Y1. X1 $
$ k = 10\times 3 = 30 $
$ Y2 = \dfrac{k}{X2} $
We know k = 30
$ Y2 = \dfrac{30}{6} $
$ Y2 = 5 $
