- Home
- >
- Construct a Line Segment – Explanation & Examples
Construct a Line Segment – Explanation and Examples
 To construct a line segment connecting two points, you need to line up a straightedge with two points and trace. Constructing a new line segment congruent to another involves creating an equilateral triangle and two circles.
To construct a line segment connecting two points, you need to line up a straightedge with two points and trace. Constructing a new line segment congruent to another involves creating an equilateral triangle and two circles.
The construction of a line segment between any two points is Euclid’s first postulate. Creating a line congruent to a given line is his second proposition. To do the construction and prove that the two lines are indeed congruent, we must first familiarize ourselves with proposition 1, which involves creating an equilateral triangle.
Before moving forward, make sure you review the foundations of geometric construction.
This topic includes:
- How to Construct a Line Segment
- How to Construct a Congruent Line Segment
How to Construct a Line Segment
Euclid’s first postulate states that a line can be drawn between any two points.
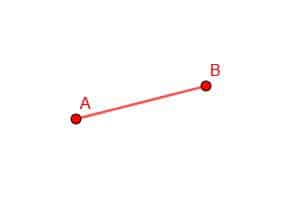
That is, as long as we have two points, we can construct a line segment. To do this, we line up the edge of the straightedge with the two points and draw a line.
It is also possible to copy a line segment that already exists. That is, we can construct a congruent line segment.
How to Construct a Congruent Line Segment
It is also possible to make a congruent copy of a line that already exists.
There are two main ways we can do this. First, we can copy a line that already exists so that the new line has a particular end point. We can also cut off a longer line segment to equal the length of a shorter line.
In fact, these two constructions are the second and third propositions in the first book of Euclid’s Elements. To do them, however, we need to first look at proposition 1. This tells us how to create an equilateral triangle.
How to Construct an Equilateral Triangle
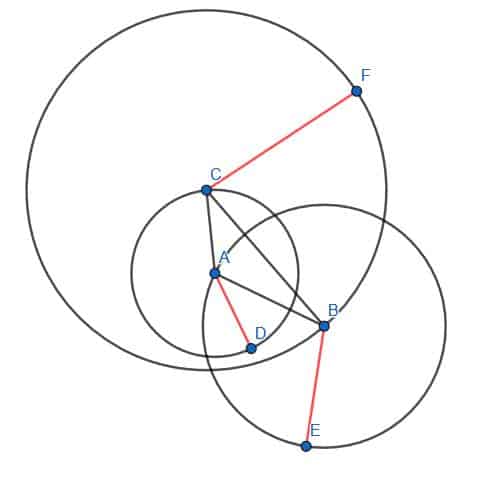
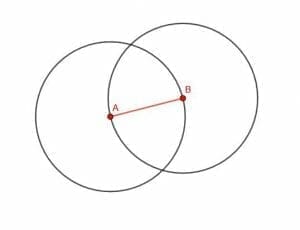
We begin with a line, AB. Our goal is to create an equilateral triangle with AB as one of the sides. By definition, an equilateral figure has sides that are all the same length. Consequently, all of the sides of the triangle we construct will be lines congruent to AB.
We begin by drawing two circles with our compass. The first will have center B and distance Ba. The second will have center A and distance AB.
Now, label either of the two intersection points for the circles as C. Then, connect AC and BC. The triangle ABC is equilateral.
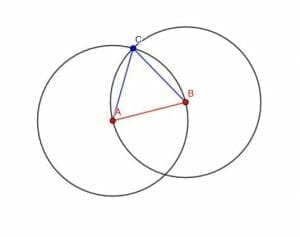
How do we know this?
BC is a radius of the first circle we drew, while AC is a radius of the second circle we drew. Both of these circles had a radius of length AB. Therefore, BC and AC both have length AB, and the triangle is equilateral.
Construct a Congruent Segment at a Point
If we are given a point line AB and a point D, it is possible to construct a new line segment with an endpoint at D and length AB.
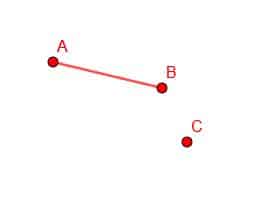
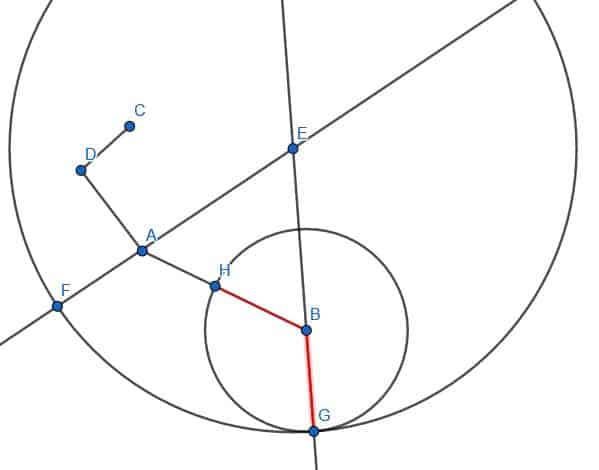
To do this, we first connect the point B with C.
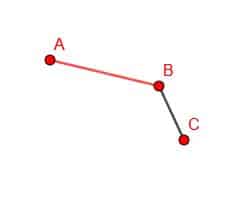
Then, construct an equilateral triangle on the line BC. Since we already know how to do this, we don’t have to show the construction lines. This also makes the proof easier to follow because the figure is less cluttered.
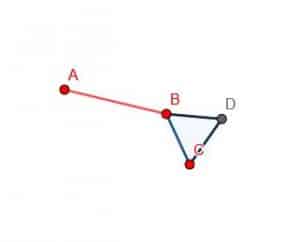
Then, we can make another circle with center B and radius BA. After that, extend the line DB so that it intersects this new circle at E.
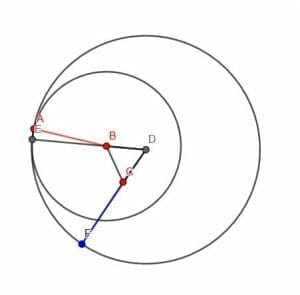
Next, we construct a circle with center D and radius DE. Finally, we can extend DC so that it intersects this circle at a point F. CF will have the same length as AB.
How do we know this?
The radius of the circle with center D is DE. Notice that DE is made up of two smaller line segments, DB and BE. Since BE is a radius of the circle with center B and radius AB, BE has the same length as AB.
The segment DB is a leg of the equilateral triangle, so its length is equal to BC. Therefore, the length of DE is DB+BE=BC+AB.
Now, consider the line segment DF. This is also a radius of the circle with center D, so its length is equal to DE. DF is made up of two parts, DC and CF. DC is equal in length to BC because they are both parts of an equilateral triangle.
Therefore, we have AB+BC=DE=DF=DC+CF=BC+CF.
That is, AB+BC=BC+CF. Therefore, AB=CF.
Cut a Shorter Segment from a Longer Segment
Using the ability to construct a congruent line at a point, we will cut off a section of a longer line segment equal to the length of a shorter segment. We begin with a longer line segment CD and a shorter segment AB.
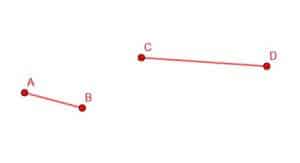
Next, we copy the segment AB and construct a congruent segment CG. Note that we do not have control over the orientation of CG, so it will, in all probability, not line up exactly with CD.

Finally, we draw a circle with center C and radius CG. Then, we can identify the point, H, where the circumference of the circle intersects CD. CH will be equal to AB in length.
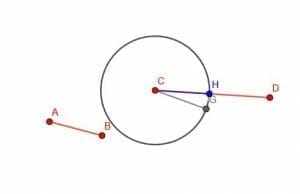
The proof of this is pretty simple. CH is a radius of the circle with center C and radius CG. Therefore CH=CG. But we already know that CG=AB. Therefore, by the transitive property, CH=AB.
Examples
This section will present some examples of how to connect line segments and how to construct congruent line segments.
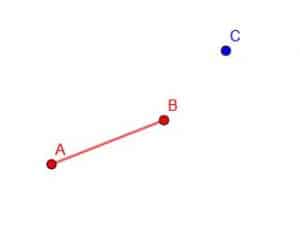
Example 1
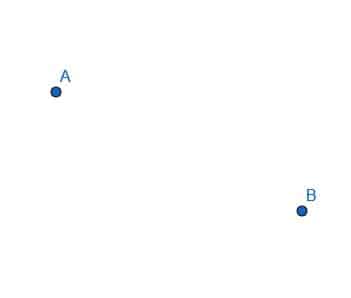
Connect points A and B with a line segment.
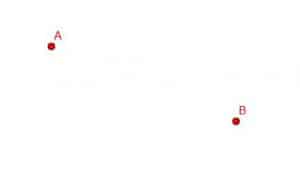
Example 1 Solution
In this case, we need to line up our straight edge with the points A and B and trace, as shown.

Example 2
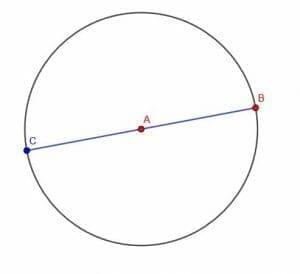
Construct a line segment congruent to AB.

Example 2 Solution
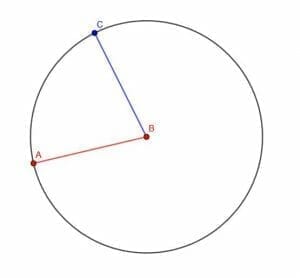
We are not given any other points in our figure, so we can construct the congruent segment anywhere we would like.
The easiest thing to do then is to make AB the radius of a circle with center B. Then, we can draw a line segment from B to any point, C, on the circle’s circumference.
Such a line segment, BC, will also be a radius of the circle, so it will be equal in length to AB.
Example 3
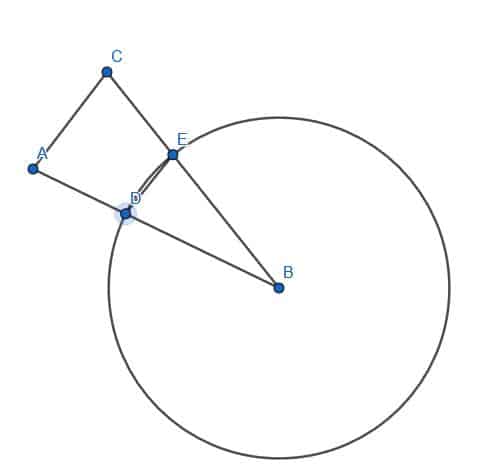
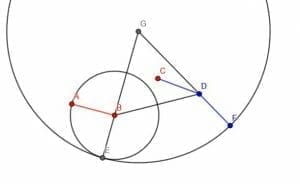
Construct a lines segment congruent to AB with endpoint D.
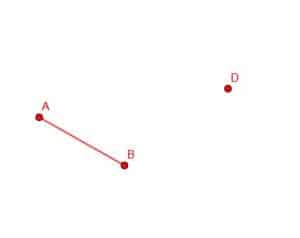
Example 3 Solution
We need to remember the steps for constructing a congruent line segment at a point to do this.
First, we connect BD.
Then, construct an equilateral triangle BDG.
Next, we create a circle with radius AB and center B. If we extend the segment GB, it intersects with this circle, and we call the intersection E.
Then, we can create a circle with center G and radius GE. We then extend GD until it intersects this circle and calls that point C.
CD will be equal in length to AB.
Note: It is important to draw full circles when proving a geometric construction, but arcs are generally fine for the construction itself. In the figure, only part of the circle with center G and radius GE is shown.
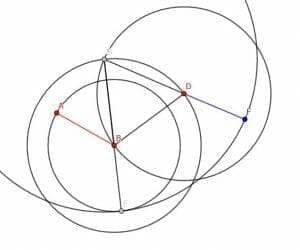
Example 4
Construct a line segment double the length of AB.

Example 4 Solution
We cannot simply copy the line segment and make its new endpoint A because we do not have control over the congruent segment’s orientation.
Instead, we can construct a circle with center A and radius AB. We can then extend the segment in the direction of A until it intersects the circle’s circumference at point C. Since AC and AB are both radii of the circle, they have the same length. Therefore, BC is double the length of AB.
Example 5
Construct a line segment congruent to AB with the end point at C. Then, put another line segment congruent to AB at the new end point, D.
Example 5 Solution
Essentially, we have to do multiple iterations of constructing a congruent segment.
First, construct a congruent segment at C, as we did in example 3.
Then, designate D to be the other end point.
Now, we do what we did before. Construct a segment BD. Then, create an equilateral triangle. Next, make a circle with center B and radius AB. We can then extend the segment GB so that it intersects with this new circle at E. Next, we make a circle with center G and radius GE. Finally, we extend GD so that it intersects with the new circle at F.
Practice Question
![]()
Open Problems
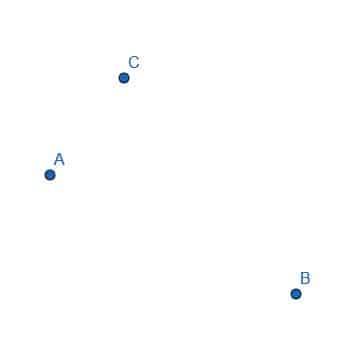
- Construct a line segment AB.

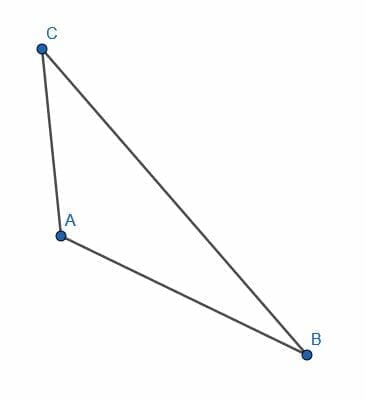
- Create line segments to create a triangle ABC.

- Construct a line segment congruent to each side of the triangle ABC.

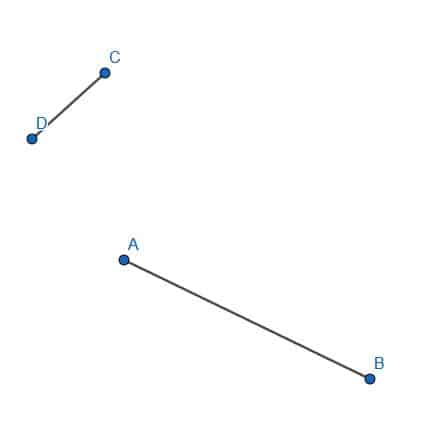
- Cut off a segment of AB equal to the length of CD.

- Construct an isosceles triangle inside the triangle ABC with B as one of the vertices.