• Home
  • >
  • Construct Parallel Lines – Explanation & Examples
  

Construct Parallel Lines – Explanation and Examples

Construct Parallel LinesConstructing a line parallel to a given line that goes through a given point involves knowing some facts about parallel lines and copying angles.

To do this, we will need to construct a transversal. This is a line that crosses two parallel lines. Several pairs of equal angles are created when we make such a line. Then, as long as we know how to copy angles, we can use this fact to create parallel lines.

Before moving on in this section, it is good to review construction and all of the previous constructions we have made since they build on each other.

In this section, we will cover:

  • How to Construct a Parallel Line
  • How to Construct a Parallel Line Through a Point
  • Constructing Congruent Angles

 

How to Construct a Parallel Line

There are several creative ways to construct parallel lines without needing to copy an angle.

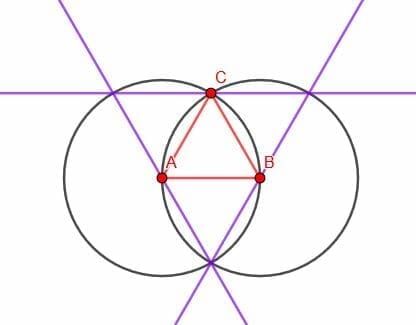
First, we can create two equilateral triangles that are the vertical mirror image of each other. The bases of two such triangles would be parallel. However, we can only create such parallel lines at given intervals.

We can also use what we know about perpendicular lines to create parallel ones. A line that is perpendicular to a line perpendicular to a given line is parallel to the given line.

There is another way to make a line parallel to a given line that goes through a given point. Doing this, however, requires that we know a little bit about the angles formed when a transversal line cuts two parallel lines.

Parallel Lines and Transversals

A transversal is a line or line segment that intersects two parallel lines, as shown.

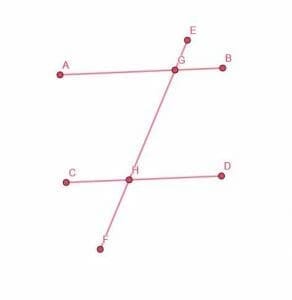
Transversal 1

This figure creates several pairs of angle relationships. First of all, the angles FHD, CHG, EGA, and BGH are all congruent. Likewise, the angles DHF, GHD, AGH, and EGB are all congruent. Additionally, the angles from “group 1” and “group 2” are supplementary. That is, their measures add up to 180 degrees.

Euclid also proves that if a third line cuts two lines and the angles created meet the specifications outlined in the previous paragraph, then the two original lines are parallel. That is, knowing these angle measures is enough to prove two lines are parallel to each other.

How to Construct a Parallel Line Through a Point

We can now use this information to help us construct a line parallel to a given line that goes through a point.

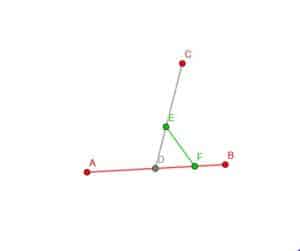
Let’s let AB be the given line and let C be the point.

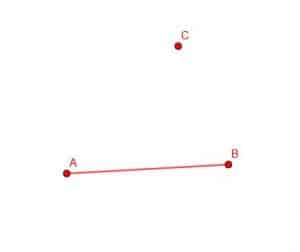
Given line and point for parallel lines

We start by picking a point at random on AB, which we will call D. Then, we connect D and C.

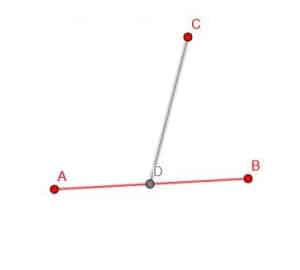
Line CD for proof of 1.31

Now, we will use the properties of angles and transversals to construct the parallel line. First, however, we need to go over how to copy an angle.

Constructing Congruent Angles

To copy an angle, we need to construct a triangle on the angle. We’ll do this with angle CDB as shown.

Triangle for copying an angle

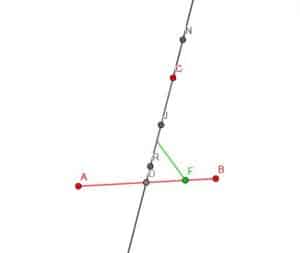
Next, we need to extend the line CD. Then, on the longer line, cut off sections equal in length to EF, ED, and DF. We want to do this in a way such that the segment equal in length to ED has C as an endpoint.

Step 2 Construct angle

Here, the segment RJ has the same length as EF, CJ the same as ED, and CN the same as DF.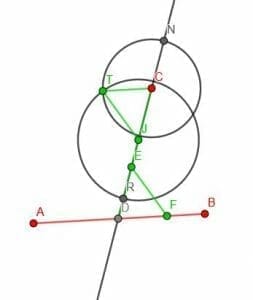Copy a Triangle and angle 1

If we create two circles, one with center C and radius CN and the other with center J and radius JR, they will intersect. Let’s call this point T. If we connect CT and JT, we will create a triangle. This triangle, JCT is equal to EDT. We can imagine flipping the triangle EDT vertically and then horizontally and then shifting it upwards to get this new triangle.

How do we know these triangles are the same? Since JT is a radius of the circle with center J, its length is equal to the radius, JR, which we constructed to be equal to EF. Likewise, since CT is a radius of the circle with center C, its length is equal to CN, which we constructed to be equal to DF. Euclid previously proved that, given three side lengths that satisfy the triangle inequality, only one triangle could be constructed. Therefore, the corresponding angles of these two triangles are congruent.

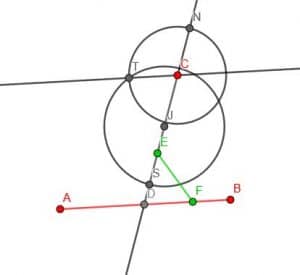
Specifically, EDF is equal to JCT. If we draw a line extending CT, this line is parallel to AB. We know this because the transversal CD creates two angles, EDF and JCT, which are equal. Euclid calls these angles “alternate angles,” and showing they are equal is sufficient to show that the lines are parallel.

Parallel Constructed Lines

Examples

In this section, we will go over common examples of problems involving constructing parallel lines.

Example 1

If alpha and beta are equal, are the following three lines parallel? How do you know?

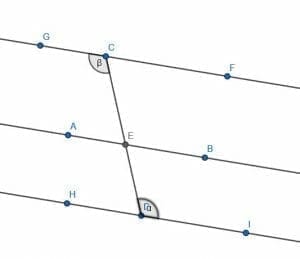
Example 1 Problem Parallel Lines

Example 1 Solution

If angle alpha and angle beta are equal, they are what Euclid calls “alternate angles.” If a line cuts through two lines and makes the alternate angles equal, it is sufficient to know that the two lines are parallel to each other.

What about the third line, the one in the middle?

It looks like this line might be parallel to the other two. Unfortunately, however, the picture does not tell us anything about the angles formed when the transversal cuts this line. Thus, we cannot make a definite statement either way about whether this line is parallel to the other two.

Example 2

Create pairs of parallel lines using equilateral triangles.

Example 2 Solution

We can use facts about equilateral triangles and facts about parallel lines to construct certain parallel lines.

In particular, equilateral triangles will have sides that are all the same length and angles that are all the same.

When we construct one equilateral triangle, we create two circles. One will have center A and distance AB, while the other will have center B and distance BA (assuming AB is our original line segment). When we construct the triangle, however, we construct a third point, C.

We can then use this point to make an additional circle, namely one with center C and distance CA. B will also lie on the circumference of this circle because B and A are equidistant from C.

This new circle intersects with each of the originals. We can then label these points G and D. If we connect each of these points to C, connect G to A, and connect D to B, we will form two new triangles that are equal to the original triangle ABC.

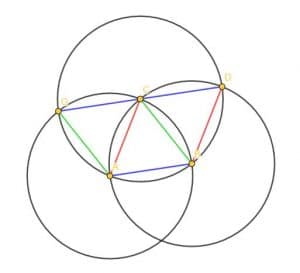
Some Equilateral Triangles

How do we know that all of the blue lines are parallel to each other, all the red lines are parallel to each other, and all of the green lines are parallel to each other?

Consider the blue lines first. Note that the line CA cuts the blue lines AB and GD. When it does, it forms the angles GCA and CAB, which are alternate angles. These are also angles of an equilateral triangle, so they are consequently equal. As we said above, showing that alternate angles are equal is sufficient to show that the two lines are parallel.

Likewise, the red lines are cut by CB and the green lines by CA. In either case, the transversal line forms alternate angles that are equal to the angle inside an equilateral triangle. Consequently, the green lines are parallel to each other, and the red lines are parallel to each other.

We can then do the same with the points D and G, making them the center of circles with radii DC and GC. Continuing this pattern and filling in the triangles formed by using the intersections as vertices gives us the pattern below. All blue lines are parallel, all green lines are parallel, and all red lines are parallel.

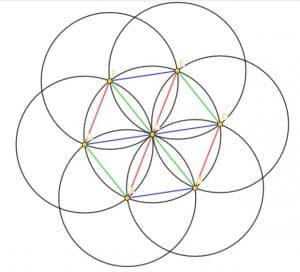
Parallel Lines Created with Equilateral Triangles

Example 3

Construct parallel lines by constructing a line perpendicular to a perpendicular line to the given line.

Given Line for Example 3

Example 3 Solution

We already know how to construct a line perpendicular to a given line. We’ll first construct a line perpendicular to AB at a point C.

Then, we can pick a point E on this new line and construct another perpendicular line segment. We will call this segment ED.

Now, note that DEC is a right angle, as is ECA. Since these are alternate angles formed when the line EC cuts the lines ED and AB and they are equal, ED is parallel to AB.

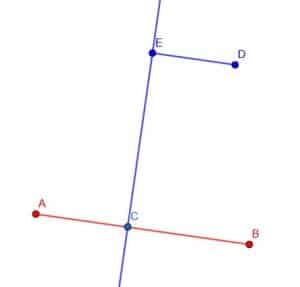
Solution to Example 3 Constructing Parallel Lines 1

Example 4

Construct a parallelogram that has AB and BC as two of its sides.

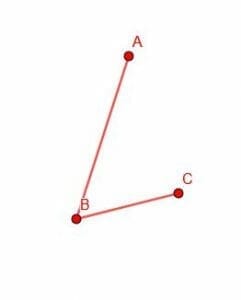
Prompt for Example 4 Construct Parallel Lines

Example 4 Solution

We will have to construct a line parallel to AB at C and a line parallel to BC at A.

We will follow the same procedure as before, beginning with the construction of a line parallel to AB at C.

BC is already connected, so we create a triangle EF as shown.

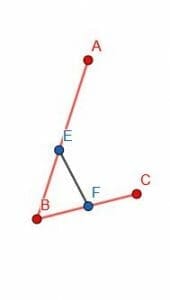
Step 2 for Example 4 Construction Parallelogram

Next, we extend CB and cut segments equal to EF, FB, and EB. We want the segments of length FB and EB to intersect at C, as shown.

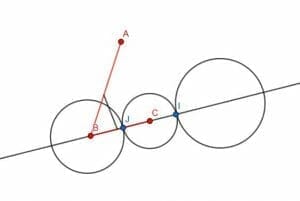
 Step 3 for Example 4 Construction Parallelogram

We can then inscribe circles centered at C with radius CB and centered at J with radius JI. If we draw a line through these two circles’ intersection, which we will call K and C, we get a line parallel to AB.

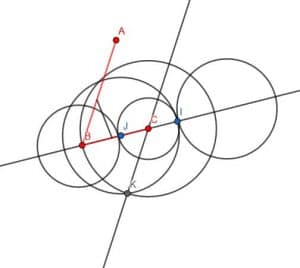
Step 5 Construction Example 4 Parallelogram

We can do the same thing to construct a line parallel to BC at A. This line will intersect the line we constructed parallel to AB at C. If we call this intersection D, we end up with a figure like the one shown below.

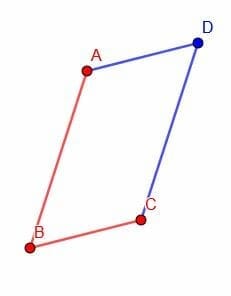
Parallelogram for Example 4 Construct Parallel Lines

Example 5

Construct a line parallel to the given line through the point C.

Example 5 Paradox Parallel Lines

Example 5 Solution

This example actually serves to illustrate one constraint about constructing parallel lines. To do that, we have to have a given point that does not lie on the original line.

Why?

This is because, by definition, parallel lines are lines that never intersect in the Euclidean plane. If a parallel line ran through C and the original line, the two lines would intersect, making them not parallel in the first place.

Therefore, there is no solution.

 

Practice Questions

1. True or False: Parallel lines are lines that may or may not intersect in the Euclidean plane

2. True or False: Two parallel lines will always the same distance apart.

3. True or False: Suppose that $\angle EMA = \angle DNF$, the lines $AB$ and $CD$ are parallel.

Constructing a Parallel Line 2

4. True or False: Suppose that $\angle EMA = \angle EMB$, the lines $AB$ and $CD$ are parallel.

Constructing a Parallel Line 2

5. True or False: If the lines $AB$ and $CD$ are parallel, the line $EF$ are also parallel to the two lines.

Constructing a Parallel Line 2


 

Open Problems

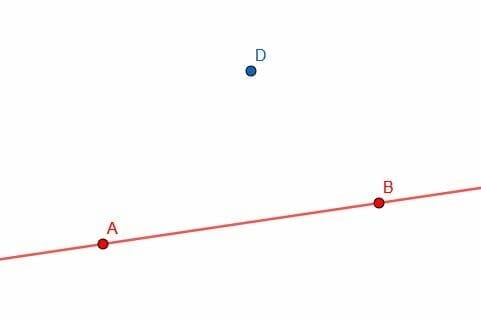
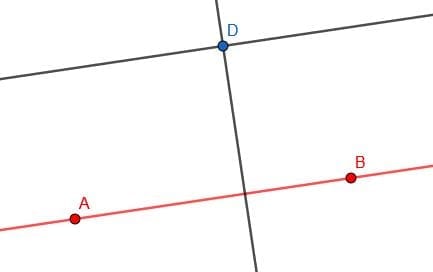
  1. Construct a line perpendicular to $AB$ that passes through $D$. Then, construct a line parallel to $AB$ that passes through $D$. What is the relationship between these two lines?
    Practice Problem 1 Parallel Lines
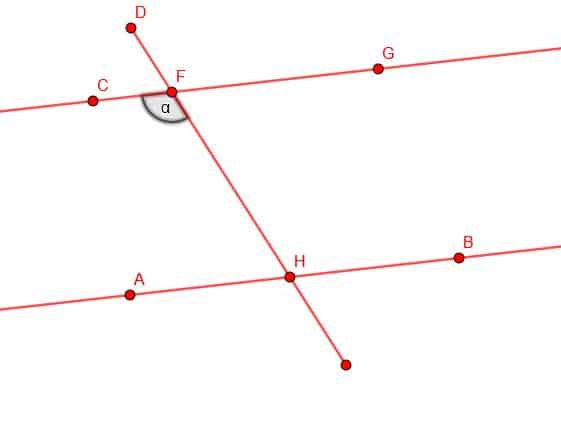
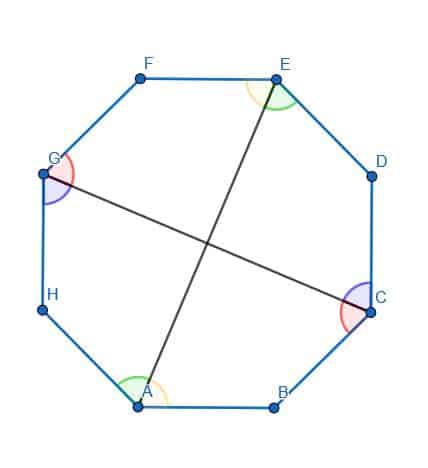
  2. Identify all of the angles that are parallel to the angle $\alpha$.
    PP2 Prompt Parallel Lines 1
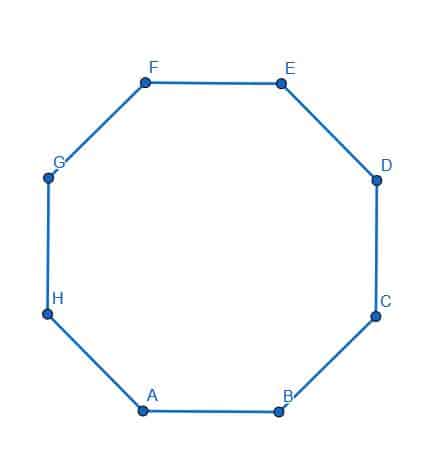
  3. PP3 Parallel Lines

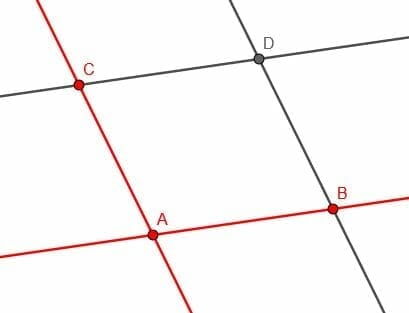
    Construct as many objects as needed to prove that $AB$ is parallel to $FE$, $GF$ is parallel to $BC$, $GH$ is parallel to $DC$, and $HA$ is parallel to $ED$.

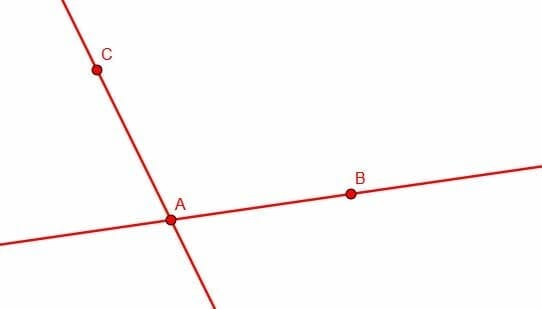
  4. PP4 Prompt Parallel Lines
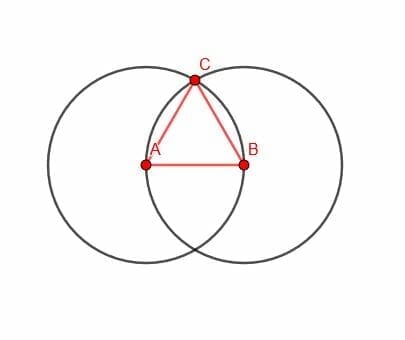
    Construct a line parallel to $AB$ through $C$ and a line parallel to $CA$ through $B$. What shape is enclosed by the lines?
  5. PP5 Prompt Parallel Lines
    Construct a line parallel to $AB$ through $C$, a line parallel to $CB$ through $A$, and a line parallel to $CA$ through $B$.

Open Problem Solutions

  1. These two constructed lines are perpendicular to each other.
    Practice Problem 1 Parallel Lines Solution
  2. The angles $DFG$, $AHE$, and $FHB$, are all equivalent to the given angle, $\alpha$.
  3. PP3 Solution Parallel Lines

    The pairs of red angles prove that $BC$ is parallel to $GF$, the pairs of blue angles prove that $DC$ is parallel to $GH$, the pairs of green angles prove $HA$ is parallel to $ED$, and the pairs of golden angles prove $AB$ is parallel to $EF$.

  4. PP4 Parallel Lines Solution

    The enclosed space is a parallelogram.

  5. PP5 Parallel Lines Solution

Previous Lesson | Main Page | Next Lesson