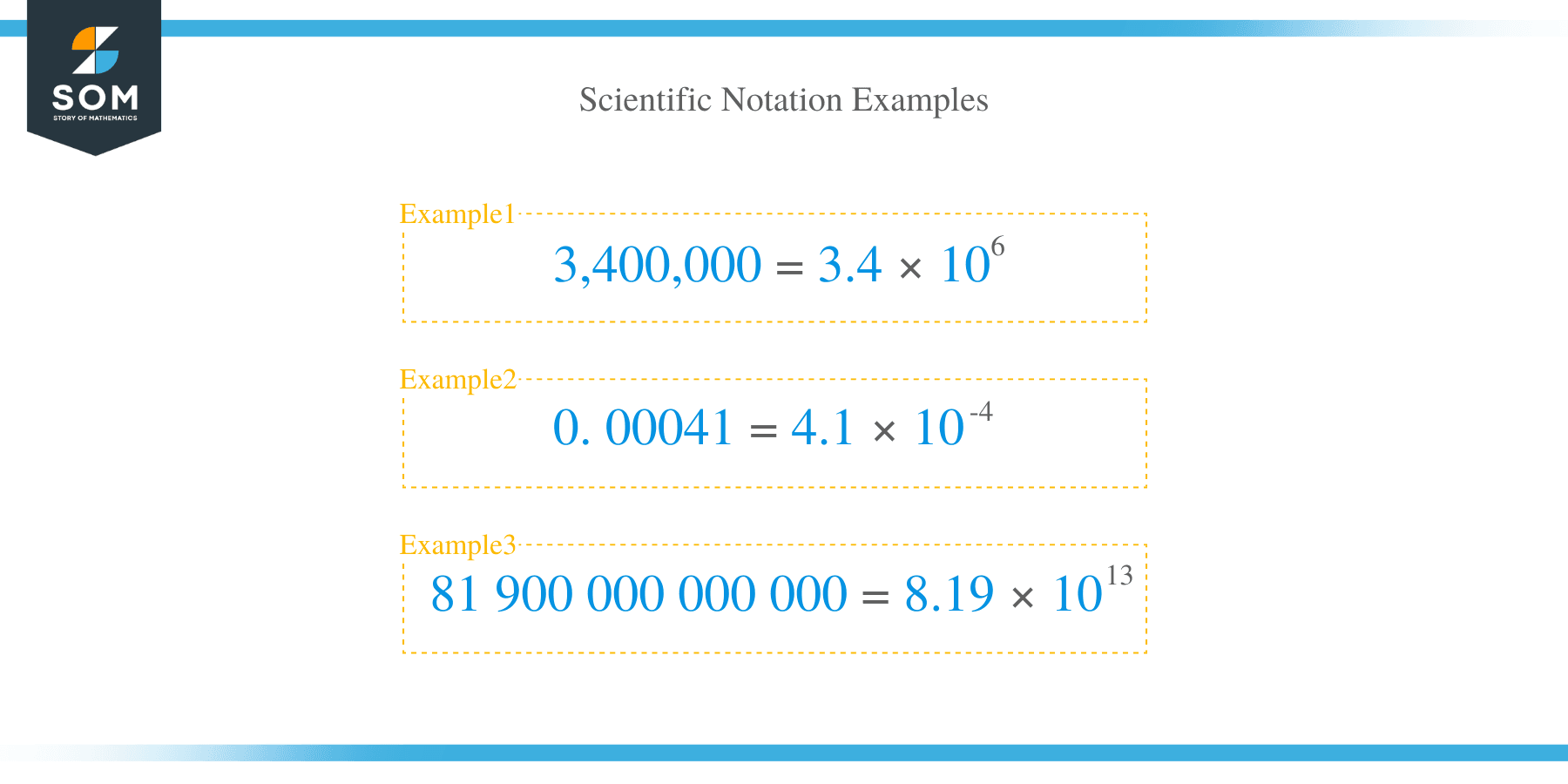Converting to Scientific Notation – Technique & Examples

Scientific notation is a technique of expressing gigantic or incredibly small numbers in a simpler form. Although scientific notation is one of the oldest mathematical operation, nowadays, it is used by engineers, scientists and mathematicians to ease the computation.

The general form of writing a number in scientific notation is: a × 10ⁿ where 1 ≤ a ≤ 10 and n is any integer. The number a which known as coefficient must be greater than 1 and less than 10.

An example of scientific notation is 2.5 x 10⁶ which is equivalent to expressing the number as 2500000. In this example, 2.5 is the coefficient and the first digit of the coefficient is known as the mantissa. The number 2 is the mantissa in 2.5 x 10^6.

How to Convert to Scientific Notation?

In this article, we shall learn the rules and procedures of converting numbers to scientific notation and therefore, you will be able to convert any number you come across on your own. Conversion of numbers to scientific notation is quite simple and easy.

Let us take a look into these steps for converting numbers to scientific notation:

• To convert a number to scientific notation, place or move the decimal point of a number until the coefficient of the number is greater than 1 and less than 10.
• Record down the coefficient (a) and count the number of steps the decimal point was moved.
• The number of steps moved (n) is taken as the exponent.
• Moving the decimal point to the right gives a negative exponent, whereas moving the decimal point to the left makes a positive exponent.

Example 1

Consider a big number 3,400,000. To convert this number into scientific notation:

• Place a decimal by counting the steps to the left until the coefficient of the number is between 1 and 9.
• Count the number of steps moved. This will be the power of the base 10.
• In this case, the coefficient is 3.4 and the 6 steps are moved.
• Multiply the coefficient by 10⁶,
• Therefore, the answer is 3. 4 x 10 ⁶

Example 2

Consider another scenario of a small number 0. 00041.In this case the scientific notation is negative because the number is less than 1.

• Move the decimal point to the right until you find the coefficient to be greater than 1 and less than 10.
• The coefficient is therefore, 4.1 and the steps moved are 4. This implies that, the power of the base 10 will be 4.
• Multiply the coefficient with the base: 4.1 x 10^-4. The negative exponent indicates that, we moved to the right,
• Thus, the answer is 4.1 x 10^-4

Example 3

Convert the following number to scientific notation:

81 900 000 000 000

• Place the decimal to the number by counting from the right to the left.
• The coefficient of the number should be between 1 and 10, and in this case 8. 19 is our coefficient
• Count the number of steps moved because this will be the power of the base 10.
• Multiply the coefficient by the base: 8.19 x 10 ¹³
• So, the answer is 8.19 x 10 ¹³