Corresponding Angles – Explanation & Examples

Before jumping into the topic of corresponding angles, let’s first remind ourselves about angles, parallel and non-parallel lines, and transversal lines.

In Geometry, an angle is composed of three parts: vertex and two arms or sides. The vertex of an angle is where two sides or lines of the angle meet, while arms of an angle are simply the angle’s sides.

Parallel lines are two or more lines on a 2-D plane that never meet or cross. On the other hand, non-parallel lines are two or more lines that intersect. A transversal line is a line that crosses or passes through two other lines. A transverse line can pass through two parallel or non-parallel lines.

What is a Corresponding Angle?

Angles formed when a transversal line cuts across two straight lines are known as corresponding angles. Corresponding angles are located in the same relative position, an intersection of transversal and two or more straight lines.

The angle rule of corresponding angles or the corresponding angles postulates that the corresponding angles are equal if a transversal cuts two parallel lines.

Corresponding angles are equal if the transversal line crosses at least two parallel lines.

The diagram below illustrates corresponding angles formed when a transversal line crosses two parallel lines:

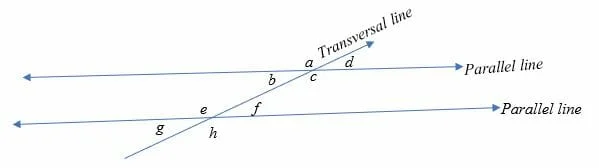
From the above diagram, the pair of corresponding angles are:

• < a and < e
• < b and < g
• < d and <f
• < c and < h

Proof of Corresponding Angles

In the figure above, we have two parallel lines.

We need to prove that.

We have the straight angles:

From the transitive property,

From the alternate angle’s theorem,

Using substitution, we have,

Hence,

Corresponding angles formed by non-parallel lines

Corresponding angles are formed when a transversal line intersects at least two non-parallel lines that are not equal, and in fact, they don’t have any relation with each other.

Illustration:

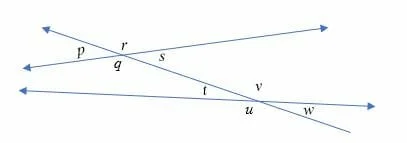
Corresponding interior angle

A pair of corresponding angles is composed of one interior and another exterior angle. Interior angles are angles that are positioned within the corners of the intersections.

Corresponding exterior angle

Angles that are formed outside the intersected parallel lines. An exterior angle and interior angle make a pair of corresponding angles.

Illustration:

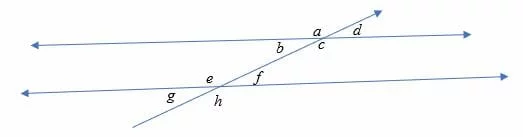
Interior angles include; b, c, e, and f, while exterior angles include; a, d, g, and h.

Therefore, pairs of corresponding angles include:

• < a and < e.
• < b and < g
• < d and < f
• < c and < h

We can make the following conclusions about corresponding angles:

• A pair of corresponding angles lie on the same side of the transversal.
• The corresponding pair of angles comprises one exterior angle and another interior angle.
• Not all corresponding angles are equal. Corresponding angles are equal if the transversal intersects two parallel lines. If the transversal intersects non-parallel lines, the corresponding angles formed are not congruent and are not related in any way.
• Corresponding angles form are supplementary angles if the transversal perpendicularly intersects two parallel lines.
• Exterior angles on the same side of the transversal are supplementary if the lines are parallel. Similarly, interior angles are supplementary if the two lines are parallel.

How to find corresponding angles?

One technique of solving corresponding angles is to draw the letter F on the given diagram. Make the letter to face in any direction and relate the angles accordingly.

Example 1

Given ∠d = 30°, find the missing angles in the diagram below.

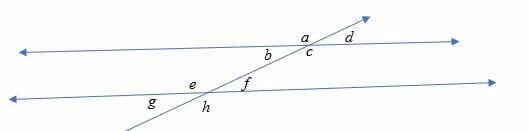
Solution

Given that ∠d = 30°

∠d = ∠b (Vertically opposite angles)

Therefore, ∠b = 30°

∠b = ∠ g= 30° (corresponding angles)
Now, ∠ d = ∠ f (Corresponding angles)

Therefore, ∠f = 30°
∠ b + ∠ a = 180° (supplementary angles)

∠a+ 30° = 180°

∠ a = 150°

∠ a = ∠ e = (corresponding angles)

Therefore, ∠e = 150°

∠d = ∠h = 30° (corresponding angles)

Example 2

The two corresponding angles of a figure measure 9x + 10 and 55. Find the value of x.

Solution

The two corresponding angles are always congruent.

Hence,

9x + 10 = 55

9x = 55 – 10

9x = 45

x = 5

Example 3

The two corresponding angles of a figure measure 7y – 12 and 5y + 6. Find the magnitude of a corresponding angle.

Solution

First, we need to determine the value of y.

The two corresponding angles are always congruent.

Hence,

7y – 12 = 5y + 6

7y – 5y = 12 + 6

2y = 18

y = 9

The magnitude of a corresponding angle,

5y + 6 = 5 (9) + 6 = 51

Applications of Corresponding Angles

There exist many applications of corresponding angles which we ignore. Observe them if you ever get a chance.

• Usually, windows have horizontal and vertical grills, which make multiple squares. Each vertex of the square makes the corresponding angles.
• The bridge stands on the pillars. All pillars are connected in such a way that corresponding angles are equal.
• The railway tracks are designed so that all the corresponding angles are equal on the track.