Curl Vector Field – Definition, Formula, and Examples

Through the curl of a vector field, we can now study how fluid rotates and electric flux behaves. We’ll need the curl when studying any quantity and relationships represented by vector fields.

The curl of a vector field allows us to measure the rotation of a vector field. The resulting value of a vector’s curl can tell us whether a vector field is rotational or not.

In this article, we’ll show you what curls represent in the physical world and how we can apply the formulas to calculate the curl of a vector field. We’ll also provide examples and problems for you to work on and better understand this important measure.

What Is the Curl of a Vector?

The curl of a vector field, $\nabla \times \textbf{F}$, at any given point, is simply the limiting value of the closed line integral projected in a plane that is perpendicular to $\widehat{\textbf{n}}$. Mathematically, we can define the curl of a vector using the equations shown below.

\begin{aligned} curl\phantom{x} \textbf{F} &= \nabla \times \textbf{F}\\&= \lim_{s \rightarrow 0} \oint_{C} \dfrac{\textbf{F} \cdot \textbf{dl}}{\partial s}\end{aligned}

Now, how do we interpret this as actual quantities? The curl of a vector field, $\nabla \times \textbf{F}$, has a magnitude that represents the maximum total circulation of $\textbf{F}$ per unit area. This occurs as the area approaches zero with a direction that is normal with respect to the area.

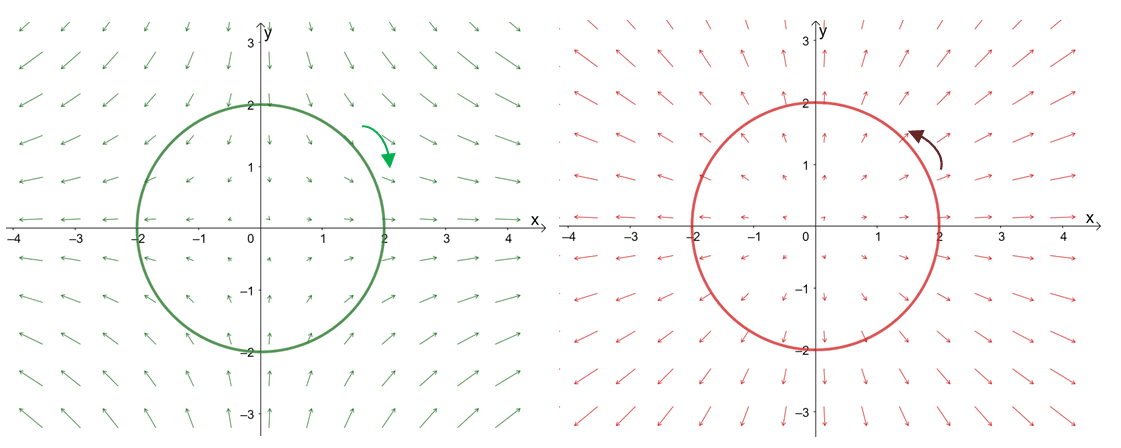
The curl of a vector allows us to measure the spinning action present in a vector field. In general, we can interpret the curl of a vector field as the angular velocity at any point contained within the given vector field. This means that when the curl of a vector field, $\nabla \times \textbf{F}$, is equal to zero, the vector field is said to be irrotational.

Let’s now write the expressions for $\nabla \times \textbf{F}$ when $\textbf{F}$ is a two-dimensional and when $\textbf{F}$ is three-dimensional.

We call $\nabla \times \textbf{F}$ as the “curl of $\textbf{F}$” or the “del cross \textbf{F}$. In the next section, we’ll learn how to apply these formulas to evaluate the curls of different vector fields.

How To Find the Curl of a Vector?

Finding the curl of a vector is straightforward: identify whether the vector field has two dimensions or three dimensions. The process will change depending on $\textbf{F}$’s components.

• If $\textbf{F} = <F_1(x, y), F_2(x, y)>$ and has two dimensions, we take the partial derivative of $F_2$ with respect to $y$ and the partial derivative of $F_1$ with respect to $x$. The difference between the two expressions will be the curl of $\textbf{F}$.
• If $\textbf{F} = <F_1(x, y, z), F_2(x, y, z), F_3(x, y, z)>$ and has three dimensions, we write down the matrix shown below as guide.

\begin{aligned}\nabla \times \textbf{F} &= \begin{vmatrix}\textbf{i} & \textbf{j} &\textbf{k} \\\dfrac{\partial}{\partial x} &  \dfrac{\partial}{\partial y}& \dfrac{\partial}{\partial z}\\F_1 &F_2  &F_3 \end{vmatrix}\end{aligned}

• Now, evaluate the matrix to return the curl of a vector.

\begin{aligned}\nabla \times \textbf{F} &=\left<\left(\dfrac{\partial F_3}{\partial y}- \dfrac{\partial F_2}{\partial z}  \right ),\left(\dfrac{\partial F_1}{\partial z}- \dfrac{\partial F_3}{\partial x}  \right ), \left(\dfrac{\partial F_2}{\partial x}- \dfrac{\partial F_1}{\partial y}  \right )\right>\end{aligned}

Let’s show you how to evaluate the curl of a vector in $\mathbb{R}^2$ and $\mathbb{R}^3$. Starting by evaluating the curl of $\textbf{F} = <y, -x>$. We have $F_1(x,y) = y$ and $F_2(x,y ) = -x$, so let’s take the partial derivatives of $F_1(x,y)$ and $F_2(x, y)$  with respect to $y$ and $x$, respectively. Subtract the two expressions to find the curl of $\textbf{F}$.

\begin{aligned}\nabla \times \textbf{F} &= \left(\dfrac{\partial F_2}{\partial x} -\dfrac{\partial F_1}{\partial y} \right )\textbf{k}\\&= \left[\dfrac{\partial }{\partial y}(-x) -\dfrac{\partial }{\partial y}(y) \right ] \textbf{k}\\&= (-1 -1) \textbf{k}\\&= -2 \textbf{k}\end{aligned}

This shows that the curl of $\textbf{F} = <y, -x>$ is a constant vector lying along the $z$-direction.

Let’s now try evaluating the curl of $\textbf{F} = <4x^2, 2z, -2x>$. This time we’re working with a three-dimensional vector, so we have the following components:

\begin{aligned}F_1 &= 4x^2\\F_2 &= 2z\\F_3&= -2x\end{aligned}

Write down the curl of $\textbf{F}(x, y,z)$ using its matrix form and eventually evaluating the partial derivatives of $F_1$, $F_2$, and $F_3$.

\begin{aligned}\nabla \times \textbf{F} &= \begin{vmatrix}\textbf{i} & \textbf{j} &\textbf{k} \\\dfrac{\partial}{\partial x} &  \dfrac{\partial}{\partial y}& \dfrac{\partial}{\partial z}\\4x^2 &2z  &-2x\end{vmatrix}\\&= \left<\left[\dfrac{\partial(-2x) }{\partial y}  – \dfrac{\partial(2z)}{\partial z}\right],\left[\dfrac{\partial (4x^2)}{\partial z}  – \dfrac{\partial(-2x)}{\partial x}\right],\left[\dfrac{\partial (2z)}{\partial x}  – \dfrac{\partial(4x^2)}{\partial y}\right]\right>\\&=\left<(0 – 2), (0 – -2), (0 – 0) \right>\\&= <-2, 2, 0>\end{aligned}
We’ve shown you how to apply the formula for the curl. Of course, the best way to understand the process of evaluating curls is through practice, so we’ve prepared more questions for you to try!

Example 1

Use the curl of $\textbf{F} = <x^2y, 2xyz, xy^2>$ to determine whether the vector field is conservative.

Solution

When the curl of a vector field is equal to zero, we can conclude that the vector field is conservative. This means that we’ll need to see whether $\nabla \times \textbf{F}$ is equal to zero or not. We have $F_1(x,y,z) = x^2y$, $F_2(x,y,z) = 2xyz$, and $F_3(x,y,z) = xy^2$, so let’s go ahead and evaluate $\nabla \times \textbf{F}$.

\begin{aligned}\nabla \times \textbf{F} &= \begin{vmatrix}\textbf{i} & \textbf{j} &\textbf{k} \\ \dfrac{\partial}{\partial x} &  \dfrac{\partial}{\partial y}& \dfrac{\partial}{\partial z}\\ x^2y &2xyz  &xy^2 \end{vmatrix}\\&= \left<\left[\dfrac{\partial(xy^2) }{\partial y}  – \dfrac{\partial(2xyz)}{\partial z}\right],\left[\dfrac{\partial (x^2y)}{\partial z}  – \dfrac{\partial(xy^2)}{\partial x}\right],\left[\dfrac{\partial (2xyz)}{\partial x}  – \dfrac{\partial(x^2y)}{\partial y}\right]\right>\\&=\left<(2xy – 2xy), (0 – y^2), (2yz – x^2) \right>\\&= <0, -y^2, 2yz -x^2>\\&\neq 0\end{aligned}

Since $\nabla \times \textbf{F}$ is not equal to zero, our vector field is not conservative.

Example 2

Evaluate the curl of $\textbf{F} = <\sin x \sin z, \cos y \cos z, \sin x \cos y>$ at the point, $\left(\dfrac{\pi}{2}, 0 , \dfrac{\pi}{2}\right)$.

Solution

Let’s first find the expression for $\nabla\times \textbf{F} = <\sin x \sin z, \cos y \cos z, \sin x \cos y>$. Here’s a summary of the calculations to find $\nabla\times \textbf{F}$.

\begin{aligned}\nabla \times \textbf{F} &= \begin{vmatrix}\textbf{i} & \textbf{j} &\textbf{k} \\ \dfrac{\partial}{\partial x} &  \dfrac{\partial}{\partial y}& \dfrac{\partial}{\partial z}\\ \sin x \sin z &\cos y \cos z  &, \sin x \cos y \end{vmatrix}\\&= \left<\left[\dfrac{\partial(\sin x \cos y) }{\partial y}  – \dfrac{\partial(\cos y \cos z )}{\partial z}\right],\left[\dfrac{\partial (\cos y \cos z)}{\partial z}  – \dfrac{\partial(\sin x \sin z)}{\partial x}\right],\left[\dfrac{\partial (\cos y \cos z)}{\partial x}  – \dfrac{\partial(\sin x \sin z )}{\partial y}\right]\right>\\&=\left<(-\sin x\cos y- -\cos y\sin z), (-\cos y\sin z- \sin z \cos x), (0 – 0) \right>\\&= <\cos y \sin z -\sin x\cos y, -\cos y\sin z – \cos x \sin z, 0>\end{aligned}

Now that we have the curl of the vector field, we can go ahead and evaluate the resulting vector function at $x = \dfrac{\pi}{2}$, $y =0$, and $z = \dfrac{\pi}{2}$.

\begin{aligned}\nabla \times \textbf{F}\left(\dfrac{\pi}{2}, 0, \dfrac{\pi}{2}\right) &= \left<\cos 0 \sin \dfrac{\pi}{2} -\sin \dfrac{\pi}{2}\cos 0, -\cos 0\sin \dfrac{\pi}{2} – \cos \dfrac{\pi}{2} \sin \dfrac{\pi}{2}, 0\right>\\&= \left<1 – 1, -1 – 1, 0\right>\\&= \left<0, -2, 0 \right>\end{aligned}

This means that the curl of the vector field at the point, $\left(\dfrac{\pi}{2}, 0 , \dfrac{\pi}{2}\right)$, is the vector, $\left<0, -2, 0\right>$ or $-2\textbf{j}$.

Practice Questions

1. Evaluate the curl of the following vector fields in $\mathbb{R}^2$.
a. $\textbf{F} = <2x, 3y>$
b. $\textbf{F}= <3x^2, 4xy>$
c. $\textbf{F}= y^3\textbf{i} -2xy \textbf{j}$
d. $\textbf{F}= \ln(xy) \textbf{i} – e^x\cos y\textbf{j}$
2. Use the curl of $\textbf{F} = <3yz, 3xz, 3xy>$ to determine whether the vector field is conservative.
3. Evaluate the curl of $\textbf{F} = <e^z\ln y, e^y\ln x, e^x \ln y>$ at the point, $\left(1, 1, 1\right)$.
4. Evaluate the curl of the following vector fields in $\mathbb{R}^3$.
a. $\textbf{F} = <2x, -4y, 3z>$
b. $\textbf{F}= < \cos x \sin y, \sin x \cos y, \cos z \sin x>$
c. $\textbf{F}= e^{xy}\textbf{i} +e^{yz}\textbf{j}+ e^{zx}\textbf{k}$
d. $\textbf{F}= \sin xy\textbf{i} + \cos yz\textbf{j}+ \sin xz\textbf{k}$

Answer Key

1.
a. $\nabla \times \textbf{F} =0 $
b. $\nabla \times \textbf{F} = 4y\textbf{k} $
c. $\nabla \times \textbf{F} = -\dfrac{ye^x \cos y + 1}{y}\textbf{k} $
d. $\nabla \times \textbf{F} = -y(3y + 2) \textbf{k} $
2. $\nabla \times \textbf{F} = 0$, so the vector field is conservative.
3. $\nabla \times \textbf{F} = \left<\dfrac{e^x}{y}, (e^z – e^x)\ln y, \dfrac{e^y}{x} -\dfrac{e^z}{y}\right>$, so at $\left(1, 1, 1\right)$, it’s equal to $<e, 0, 0>$ or $e \textbf{i}$.
4.
a. $\nabla \times \textbf{F} =0 $
b. $\nabla \times \textbf{F} = <0, -\cos x\cos z, 0> = -\cos x\cos z\textbf{j} $
c. $\nabla \times \textbf{F} = <-ye^{yz}, -ze^{xz}, -xe^{xy}> = -ye^{yz}\textbf{i} -ze^{xz}\textbf{j} -xe^{xy}\textbf{k}$
d. $\nabla \times \textbf{F} = <y \sin yz, -z \cos xz, -x \cos xy> = y \sin yz \textbf{i} -z \cos xz \textbf{j}- x \cos xy \textbf{k}$

Images/mathematical drawings are created with GeoGebra.