DeMorgan’s Laws – Explanation and Examples

In set theory, there exists a wide variety of sets. Some of the common types of sets discussed in our previous lessons include finite sets, infinite sets, universal sets, equal sets, and null sets. We also studied multiple set operations in-depth, including set union, set intersection, and set complement. 

In set theory, apart from set operations and set types, some certified set laws exist which simplify the set operations. These laws are termed as DeMorgan’s laws. 

Before diving into the concept of DeMorgan’s laws, we recommend you to go through our previous lectures first to solidify your concepts of the set union, set intersection, and set complement. 

We will be covering the following topics in this article:

• What are DeMorgan’s laws?
• Recap of the set union.
• Recap of set intersection.
• Recap of set complement.
• Proof of DeMorgan’s laws.
• How to use DeMorgan’s laws?
• Examples.
• Practice problems.

Before moving forward, you may consider refreshing your knowledge on the following prerequisites:

• Describing Sets
• Sets Notation
• Subset
• Universal Set

What are DeMorgan’s Laws?

As mentioned above, set theory is an amalgam of set operations and set types. The understanding of these multiple set operations and their inter-relationship can be quite intimidating for young mathematics enthusiasts. Therefore, to better understand and simplify the relationships between multiple set operations, DeMorgan’s laws are considered the best tools.

DeMorgan’s laws depict the relationship between the three fundamental set operations: the set union, set intersection, and the set complement. Depending on the inter-relationship between the set union and set intersection, two kinds of DeMorgan’s laws exist in set theory. 

These laws are explained below.

Type 1 DeMorgan’s Law:

Type 1 DeMorgan’s law states that the complement of the union of any two sets say A and B, is equal to the intersection of their complements. 

This type of DeMorgan’s law inter-relates any two sets’ union with their intersection via set complement operation. Consider any two finite sets, A and B. We can portray the relationship between the union and the intersection of these two sets A and B through the type 1 DeMorgan’s law, whose mathematical form is given below:

(A U B)’ = A’ ∩ B’

Type 2 DeMorgan’s Law:

The second type of DeMorgan’s law states that the complement of the intersection of any two sets says A and B, is equal to the union of their complements. 

Type 2 DeMorgan’s law is opposed to the type 1 law. This law depicts the inter-relationship between the intersection and union of any two sets through set complement operation. Consider any two finite sets, namely A and B. Their intersection can be related to their union via the second type of DeMorgan’s law. The mathematical form of this type of law is given below:

(A ∩ B)’ = A’ U B.’

Before we delve into the proofs and examples of DeMorgan’s laws, let’s do a quick revision of the fundamental set operations.

Recap of the Set Union

Although we have covered the set union’s topic in great detail in our previous lessons, here’s a quick recap of the set union to save you from any trouble. 

The union of any two sets, say A and B, is a joint set containing the elements present in both A and B. The mathematical form of the set union in set theory is given below:

A U B

The union between any two sets is indicated by the symbol ‘U’. The concept of union is restricted to two sets and can also be extended to multiple sets joined by the symbol of union. The mathematical form of the union of multiple sets is given below:

A U B U C U D…

We can express the union between any two sets in pictorial form with Venn Diagrams’ aid. The union between any two sets, say A and B, is portrayed by shading the entire region of sets A and B. The Venn diagram for the union set operation between two sets A and B is given below:

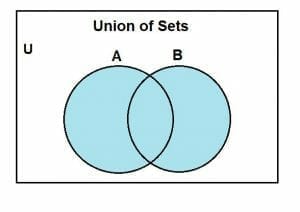
Let’s solve an example to strengthen our concept of the set union. 

Example 1

Consider the following two sets:

A = {5, 10, 15, 20}

B = {10, 20, 30, 40}

Find their union and draw the respective Venn diagram.

Solution

The union between the two sets A and B is given as:

A U B

The union is given as:

A U B = {5, 10, 15, 20} U {10, 20, 30, 40}

A U B = {5, 10, 15, 20, 30, 40}

This is the union of the two sets A and B. 

The Venn diagram representation of their union is shown below:

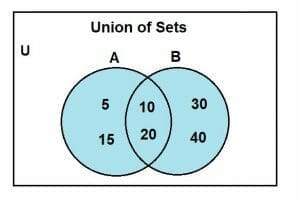
The entire shaded region shows the union of the two sets, A and B. 

Recap of the Set Intersection

Much like the set union, we have also covered the topic of set intersection in great depth in our previous lessons. However, in this article, we will only be focussing on the quick recap of set intersection. 

The intersection of any two sets, say A and B, are the common elements in both sets A and B. The mathematical form of the intersection between two sets, A and B, is given below:

A ∩ B

The intersection between two sets is opposite to the union. The union between the sets concentrates on both sets’ joint elements, but the intersection, on the other hand, is restricted to only the common elements between the sets. 

The symbol of intersection in set theory is given as ‘∩’. The intersection operation is not only limited to two sets but can also be extended to multiple sets. The intersection between multiple sets is given as:

A ∩ B ∩ C ∩ D…

The intersection between any two sets, namely A and B, is depicted through Venn diagrams. The intersection between sets A and B is portrayed through the shaded region shared by the two sets A and B. The Venn diagram for the intersection operation is given below:

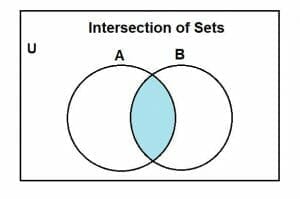
Let’s solve the same example to solidify our concept of set intersection. 

Example 2

Consider the following two sets:

A = {5, 10, 15, 20}

B = {10, 20, 30, 40}

Find their intersection and draw the respective Venn diagram.

Solution

The intersection between two sets A and B is given as:

A ∩ B

The intersection is given as:

A ∩ B = {5, 10, 15, 20} ∩ {10, 20, 30, 40}

A ∩ B = {10, 20}

This shows the intersection between the two sets, A and B.

The Venn diagram representation of their intersection is given below:

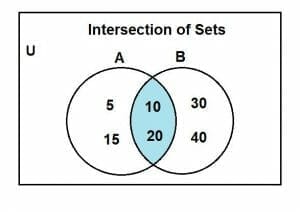
The shaded region shows the intersection of the two sets, A and B. 

Recap of the Set Complement 

The complement of a set is another vital set operation whose understanding is mandatory to understand the concept of DeMorgan’s laws. As we have extensively covered this topic before, we will only dive into the quick recap of this article’s set complement. 

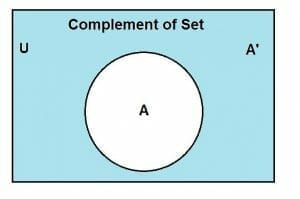
The complement of the set, let’s assume a set A, is defined as the difference between the universal set and the set A itself. 

In the set theory realm, the universal set is the fundamental parent set, and all the other sets are the subsets of the universal set. The common notation for the universal set is denoted by the symbol ‘U’. 

The difference between sets works like the mathematical operation of subtraction. The difference between any two sets, say A and B, is denoted by the subtraction sign. The mathematical expression of difference is given below:

A − B

Coming back to the definition of the set’s complement, it is the difference between the universal set and the set itself. It is denoted either by the symbol ( ‘ ). The mathematical expression for the complement of the set is given as:

A’ = U − A

We can also denote the complement of the set through the Venn diagram. The rectangular region shows the universal set U and the circular region shows the set A. The shaded region indicates the complement of A. The Venn diagram of the complement of a set is shown below:

Let’s solve an example to solidify the concept of the complement of a set.

Example 3

Find the complement of a set A = {5, 10, 15, 20} where the universal set is U = {x:x is a multiple of 5 and x<100}. Show the complement through the Venn diagram. 

Solution

To solve this, let’s first simplify the sets. We can simplify the universal set as:

U = {5, 10, 15, 20, 25, …, 100}

The complement of the set A is given as:

A’ = U − A

A’ = {5, 10, 15, 20, 25, …, 100} − {5, 10, 15, 20}

A’ = {25, 30, 35, 40, …, 100}

Where A’ denoted the complement of A. 

The Venn diagram for the complement of the set is given as:

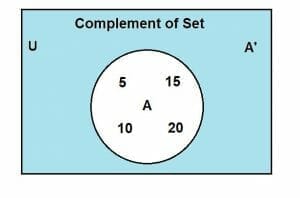
The shaded region indicates the complement of A. 

Now that we have revised our concepts of the set union, set intersection, and the set complement, let’s move onto the proofs of DeMorgan’s laws.

Proof of the DeMorgan’s Laws

DeMorgan’s laws form the foundation of the inter-relation amongst the set operations in set theory. As stated above, the set operations involved in DeMorgan’s laws include union, intersection, and complement, so understanding these three set operations in a single mathematical statement can be overwhelming for the young mathematics fanatics. Therefore, it is necessary to evaluate these laws’ proofs for their ease and for developing a simplified understanding of DeMorgan’s laws. 

Earlier, we divided DeMorgan’s laws into two types based on the inter-relation of union and intersection or vice versa. An easier approach for understanding the proofs is to evaluate the proofs individually for both the types of DeMorgan’s laws. That being said, let’s get right to the proofs. 

There are two approaches to proving DeMorgan’s laws. One of them is the mathematical approach, and the other is the Venn Diagram approach. We will be evaluating the proofs of DeMorgan’s laws through both these approaches. 

Proof of Type 1 of DeMorgan’s Law

Type 1 of DeMorgan’s law depicts the inter-relation between the union of any two sets with their intersection through set complement operation. Type 1 states that the complement of the union of any two sets, namely A and B, is equal to the intersection of their complements. 

The mathematical expression for the type 1 of DeMorgan’s law is given as:

(A U B)’ = A’ ∩ B.’

We will evaluate the proof through both the mathematical approach and the Venn diagram approach. Let’s first assess the proof through the mathematical approach. 

Mathematical Approach: 

For the mathematical approach, we will first consider the left-hand side, which is:

(A U B)’

Firstly, we will assume that there exists an element z in (A U B)’. 

Mathematically, we can state this assumption as:

z ∈ (A U B)’ 

Based on the above assumption, we can state the following relations for the element z:

z ∉ (A U B)

And, 

z ∉ A 

Also, 

z ∉ B

Excluding these relations, the only possibilities that exist for the element z are:

z ∈ A’

And, 

z ∈ B’

Since z is an element of the complement of A and the complement of B, therefore we can state the following:

z ∈ A’ ∩ B.’

Where A’ ∩ B’ is the right-hand side. 

Now, as z is both the member of the left-hand side and the right-hand side, hence:

(A U B)’ = A’ ∩ B.’

Hence, this mathematically proves type 1 of DeMorgan’s laws. 

Now let’s consider the Venn Diagram approach. 

Venn Diagram Approach:

Again, we will first proceed with the left-hand side, which is given as:

(A U B)’

Consider two sets, A and B. The Venn diagram for their union, (A U B) is given by the shaded region, which is shown below:

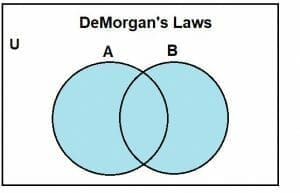
Similarly, the complement of their union, (A U B)’, will include all the region except A and B’s union. We can see this in the following Venn diagram:

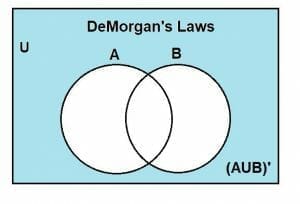
Now, let’s consider the right-hand side, which is given as:

A’ ∩ B’

The right-hand side can be divided into three segments; one is portraying A’, the other showing B’, and finally, the third one indicating A’ ∩ B’.

Let’s first consider the first two segments. 

The Venn diagram for A’ is given by the shaded region, as shown below:

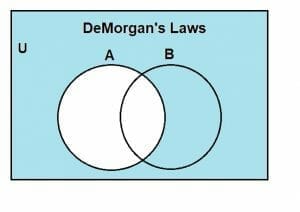
Similarly, the Venn diagram showing B’ is indicated by the shaded region, as shown below:

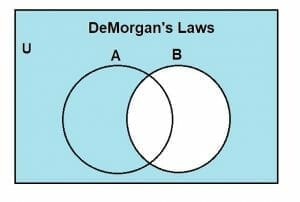
Finally, the intersection of the complements of A and B is depicted through the shaded region shown below, which is the universal set:

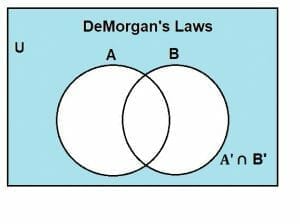
Since the Venn diagrams for the left-hand side and the right-hand side are the same, hence:

(A U B)’ = A’ ∩ B.’

Let’s solve an example for a better understanding of type 1 of DeMorgan’s laws.

Example 4

Let set U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, set A = {2, 4, 6, 8}, and set B = {1, 3, 5, 7, 9}. Prove the type 1 of DeMorgan’s laws.

Solution

Type 1 of DeMorgan’s law is given as:

(A U B)’ = A’ ∩ B.’

We will evaluate both the left-hand side and the right-hand side separately. 

Left-Hand Side:

(A U B)’ 

The union is given as:

A U B = {2, 4, 6, 8} U {1, 3, 5, 7, 9}

A U B = {1, 2, 3, 4, 5, 6, 7, 8, 9}

The complement of the union is given as:

(A U B)’ = ({1, 2, 3, 4, 5, 6, 7, 8, 9})’

(A U B)’ = U − (A U B)

(A U B)’ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} − {1, 2, 3, 4, 5, 6, 7, 8, 9}

(A U B)’ = {0, 10}

Now, let’s evaluate the right-hand side.

Right-Hand Side:
The right-hand side is given as:

A’ ∩ B’

First, let’s find the complements.

The complement of A is:

A’ = U − A

A’ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} − {2, 4, 6, 8}

A’ = {0, 1, 3, 5, 7, 9, 10}

The complement of B is:

B’ = U − B

B’ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} − {1, 3, 5, 7, 9}

B’ = {0, 2, 4, 6, 8, 10}

Now, A’ ∩ B’ is given as:

A’ ∩ B’ = {0, 1, 3, 5, 7, 9, 10} ∩ {0, 2, 4, 6, 8, 10}

A’ ∩ B’ = {0, 10}

This proves that left-hand side = right-hand side and hence:

(A U B)’ = A’ ∩ B.’

Proof of Type 2 of DeMorgan’s Law

Type 2 of DeMorgan’s law portrays the inter-relation between the intersection of any two sets with their union through set complement operation. Type 2 states that the complement of the intersection of any two sets, namely A and B, is equal to the union of their complements. 

The mathematical expression for the type 2 of DeMorgan’s law is given as:

(A ∩ B)’ = A’ U B.’

We will evaluate the proof through both the mathematical approach and the Venn diagram approach. Let’s first assess the proof through the mathematical approach. 

Mathematical Approach: 

Following the same procedure and the steps we conducted above for type 1, let’s first take the left-hand side, which is given as:

(A ∩ B)’ 

Firstly, let’s make the same assumption we made before. Consider an element y which exists in (A ∩ B)’. Mathematically, we can write this as:

y ∈ (A ∩ B)’ 

Based on this assumption, we can exclude the following relations for the element y:

y ∉ (A ∩ B)

And, 

y ∉ A

Also, 

y ∉ B

Excluding these relations, the only possibilities that exist for the element y are:

y ∈ A’

And, 

y ∈ B’

Since z is an element of the complement of A and the complement of B, therefore we can state the following:

z ∈ A’ U B.’

Where A’ U B’ is the right-hand side. 

Now, as y is both the member of the left-hand side and the right-hand side, hence:

(A ∩ B)’ = A’ U B.’

Hence, this mathematically proves type 2 of DeMorgan’s laws. 

Now let’s consider the Venn Diagram approach. 

Venn Diagram Approach:

Again, we will first proceed with the left-hand side, which is given as:

(A ∩ B)’ 

Consider any two finite sets, A and B. Their intersection, (A ∩ B),  is given by the shaded region, which is given as follows:

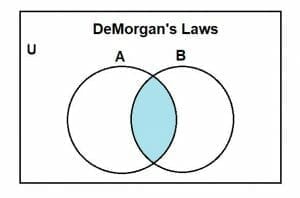
Similarly, the complement of their intersection (A ∩ B)’ is showcased by the shaded region, as shown below:

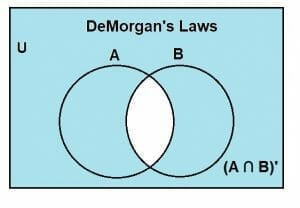
Now, let’s consider the right-hand side, which is given as  A’ U B’.

The right-hand side can be divided into three segments; one is showing A’, the other indicating B’, and the third one showcasing  A’ U B’. 

The complement of A, A’ is indicated by the shaded region, which is shown below:

Similarly, the complement of B, B’ is shown by the shaded region given below:

And finally, the union of the complement, A’ U B’, is given by the shaded region indicated as:

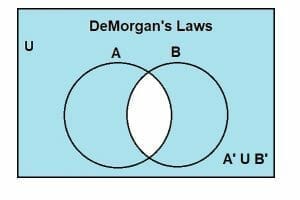
Since the Venn diagrams for the left-hand side and the right-hand side are the same, hence:

(A ∩ B)’ = A’ U B.’

Let’s solve the same example for a better understanding of type 2 of DeMorgan’s laws.

Example 5

Let set U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, set A = {2, 4, 6, 8}, and set B = {1, 3, 5, 7, 9}. Prove the type 2 of DeMorgan’s laws.

Solution

Type 2 of DeMorgan’s law is given as:

(A ∩ B)’ = A’ U B.’

We will evaluate both the left-hand side and the right-hand side separately. 

Left-Hand Side:

(A ∩ B)’ 

Let’s first the intersection of A and B given as:

(A ∩ B)

So, 

(A ∩ B) = {2, 4, 6, 8} ∩ {1, 3, 5, 7, 9}

(A ∩ B) = Ⲫ

Now, let’s find the complement of the intersection, which is given as:

(A ∩ B)’ = U − (A ∩ B)

(A ∩ B)’ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} − {Ⲫ}

(A ∩ B)’ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

Now, let’s evaluate the right-hand side.

Right-Hand Side:

A’ U B’

Let’s first find the complements:

The complement of A is:

A’ = U − A

A’ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} − {2, 4, 6, 8}

A’ = {0, 1, 3, 5, 7, 9, 10}

The complement of B is:

B’ = U − B

B’ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} − {1, 3, 5, 7, 9}

B’ = {0, 2, 4, 6, 8, 10}

Now, the union of the complements is given as:

A’ U B’ = {0, 1, 3, 5, 7, 9, 10} U {0, 2, 4, 6, 8, 10}

A’ U B’ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

This proves that left-hand side = right-hand side and hence:

(A ∩ B)’ = A’ U B.’

How to use DeMorgan’s Laws?

Now that we have developed a firm understanding of DeMorgan’s laws, the next question arises, how and when to use them? 

You can use DeMorgan’s laws whenever finding the inter-relations between the multiple set operations. DeMorgan’s laws can be beneficial in that case. In some literature, these laws are also termed the ‘complement laws.’ Both are the same. The only difference is in their terms. 

The two examples solved above can be taken as a sample for solving DeMorgan’s laws. However, for further strengthening the concept, consider the following practice problems.

Practice Problems

1. Let U = {set of alphabets} and let there be two sets A and B given as A = {set of vowels} and B = {set of constants}. Mathematically prove the type 1 DeMorgan’s law.
2. Prove the above question through the Venn diagram as well.
3. Consider 3 sets given as U = {x:x is a multiple of 10 and x<50}, A = {y:y is a multiple of 2 and y<20} and B = {z:z is a multiple of 3 and z< 30}. Mathematically prove the type 2 DeMorgan’s law.
4. Prove the above question through the Venn diagram as well.
5. Think of a problem that inter-relates both intersection and union of sets. 

Answers

1. (A U B)’ = A’ ∩ B’  [True]
2. (A U B)’ = A’ ∩ B’  [True]
3. (A ∩ B)’ = A’ U B.’ [True]
4. (A ∩ B)’ = A’ U B.’ [True]
5. DeMorgan’s laws 

Previous Lesson | Main Page | Next Lesson