Derivative calculus – Definition, Formula, and Examples

The word derivative is probably the most common word you’ll be hearing when taking your first differential calculus. This entire concept focuses on the rate of change happening within a function, and from this, an entire branch of mathematics has been established.

Derivative in calculus refers to the slope of a line that is tangent to a specific function’s curve. It also represents the limit of the difference quotient’s expression as the input approaches zero.

Derivatives are essential in mathematics since we always observe changes in systems. Other fields, including physics, economics, finance, and even sports analysis, use differential calculus. This shows how important it is for us to understand the core foundation and the common derivative rules if we want to excel in our math classes and other specializations.

This article will show you the fundamental definition of derivatives and how we can derive the different derivative rules discussed in our calculus classes. We’ll also show you why it’s important that we know how to evaluate limits if we want to derive a wide range of derivatives from different functions.

What is a derivative?                

The derivative of a function ,represented by $\dfrac{dy}{dx}$ or $f^{\prime}(x)$, represents the limit of the secant’s slope as $h$ approaches zero.

In our precalculus classes, we’ve learned about secant lines and how we can calculate the rate of change between $(x, f(x))$ and $(x, f(x + h))$ using the formula for slopes.

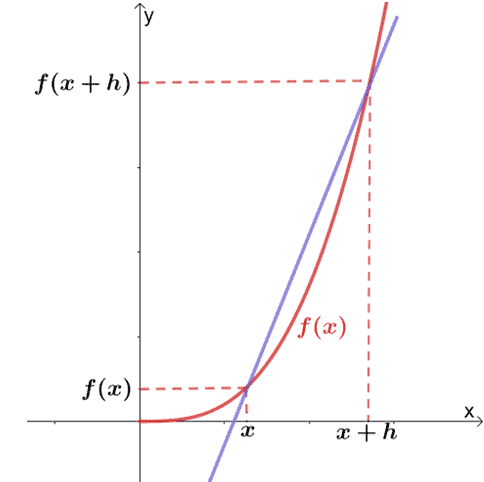
In fact, we called this the difference quotient and established that the slope of the secant line passing through a curve is equal to the formula shown below.

\begin{aligned}\dfrac{\Delta y}{\Delta x} &= \dfrac{f(x +h) – f(x)}{h} \end{aligned}

How does this relate to derivatives? The derivative of a function is simply the slope of the tangent line that passes through the function’s curve. As the distance between $x$ and $x + h$ gets smaller, the secant line that we’ve shown will approach the tangent line representing the function’s derivative.

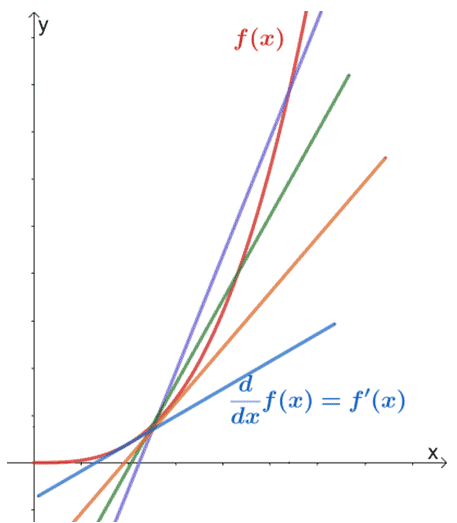
This means that the tangent line is simply the result of secant lines having a distance between $x$ and $x + h$ that are significantly small and where $h \rightarrow 0$.

This means that the slope of the tangent line simply equal to the limit of the difference quotient as $\boldsymbol{h}$ approaches zero.

\begin{aligned}m_{\text{tangent}}&= \lim_{h \rightarrow 0}\dfrac{\Delta y}{\Delta x}\\ &=\lim_{h \rightarrow 0} \dfrac{f(x +h) – f(x)}{h} \end{aligned}

This is the fundamental definition of derivatives. We denote derivatives as $\dfrac{dy}{dx}$, which represents its very definition.

\begin{aligned}\dfrac{d}{dx} f(x)&= \dfrac{dy}{dx} \\&=\lim_{h \rightarrow 0} \dfrac{f(x +h) – f(x)}{h} \end{aligned}

We can also represent the derivative of $f(x)$ as either $f’(x)$ or $y’$. This is also known as the first derivative of the function.  

How to find the derivative of a function?                

When a function is differentiable, we can find its derivative using its definition. Recall that the derivative is represented by $\dfrac{dy}{dx}$ or $f’(x)$ and can be determined using the formula shown below.

\begin{aligned}\dfrac{dy}{dx} &=\lim_{h \rightarrow 0} \dfrac{f(x +h) – f(x)}{h} \end{aligned}

This means that it’s important to find the difference quotient of the function first and then limit the resulting function as $h$ approaches $0$. Here are some steps to guide you in evaluating the derivatives of a function using its core definition:

• Find the expression for $f(x + h)$ and $f(x)$.
• Simplify the expression and cancel common factors whenever possible.
• Evaluate the resulting expression’s limit as $h \rightarrow 0$.

Let’s say we want to determine $\dfrac{d}{dx} 1 – x^2$. We’ll have to determine its difference quotient first.

\begin{aligned} f(x +h) &= [1 -(x + h)^2]\\&= 1- (x^2 + 2xh + h^2)\\f(x)&= 1- x^2\\\\\dfrac{d}{dx} (1 – x^2) &= \lim_{h \rightarrow 0} \dfrac{f(x + h) – f(x)}{h}\\&=\lim_{h \rightarrow 0} \dfrac{[1 – (x^2 + 2xh + h^2)] – (1- x^2)}{h}\\&=\lim_{h \rightarrow 0} \dfrac{1 – x^2 – 2xh – h^2 – 1+ x^2}{h}\\&=\lim_{h \rightarrow 0} \dfrac{- 2xh – h^2 }{h}\\&=\lim_{h \rightarrow 0} \dfrac{-h(2x + h)}{h} \\&=\lim_{h \rightarrow 0} –(2x +h) \end{aligned}

Now that we have the simplified expression, we can evaluate the limit of $-(2x + h)$ as $h \rightarrow 0$.

\begin{aligned} \dfrac{d}{dx} ( 1 -x^2) &= \lim_{h \rightarrow 0} -2x +h\\&= -2x + 0\\&= -2 \end{aligned}

This means that the derivative of the function, $y = 1-x^2$, is equal to $-2x$. In other notations, we have, $y’ = -2x$, $f’(x) = – 2x$, or $\dfrac{dy}{dx} = -2x$.

This process is used repeatedly to derive our long list of derivative rules. Knowing how to find the derivative of functions in this method will help you appreciate our established derivative rules. For now, let’s try more examples and know the definition of the derivative by heart.

Example 1

Find the derivative of $g(x) = \dfrac{2x}{x – 4}$ using the definition of derivative.

Solution

We’ll always go back to the derivative’s fundamental definition to find $\dfrac{dy}{dx}$.

\begin{aligned}g’(x) &= \dfrac{d}{dx} g(x)\\&= \lim_{h \rightarrow 0} \dfrac{g(x +h) – g(x)}{h} \end{aligned}

Let’s simplify the expression for $\dfrac{g(x +h) – g(x)}{h}$.

\begin{aligned} g(x + h) &= \dfrac{2(x+ h)}{[(x + h) – 4)]}\\&= \dfrac{2(x + h)}{x +h – 4}\\g(x) &= \dfrac{2x}{x  -4}\\\\\dfrac{dy}{dx} &= \lim_{h \rightarrow 0} \dfrac{g(x +h) – g(x)}{h}\\&= \lim_{h \rightarrow 0} \dfrac{\dfrac{2(x + h)}{x + h  -4} – \dfrac{2x}{x  -4}}{h} \end{aligned}

To simplify the complex rational expression, we can add the rational expressions found in the numerator.

\begin{aligned} \dfrac{dy}{dx} &= \lim_{h \rightarrow 0} \dfrac{\dfrac{(2x + 2h) (x – 4)}{(x + h  -4)(x -4)} – \dfrac{2x(x+h -4)}{(x  -4)(x + h-4)}}{h}\\&= \lim_{h \rightarrow 0} \dfrac{1}{h} \left[\dfrac{2x^2 -8x + 2xh – 8h}{(x + h  -4)(x -4)} – \dfrac{2x(x+h -4)}{(x  -4)(x + h-4)} \right ]\\&= \lim_{h \rightarrow 0} \dfrac{1}{h}\cdot \dfrac{2x^2 – 8x  +2xh -8h -2x(x+h -4)}{(x + h  -4)(x -4)}\\&= \lim_{h \rightarrow 0} \dfrac{1}{h} \cdot \dfrac{2x^2 – 8x  +2xh -8h – 2x^2 – 2xh +8x}{(x + h  -4)(x -4)}\\&= \lim_{h \rightarrow 0} \dfrac{1}{h} \cdot \dfrac{- 8h}{(x + h  -4)(x -4)}  \end{aligned}

We can simplify the expression further then eventually evaluate the limit as $h \rightarrow 0$.

\begin{aligned} \dfrac{dy}{dx} &= \lim_{h \rightarrow 0} \dfrac{1}{h} \cdot \dfrac{- 8h}{(x + h  -4)(x -4)}\\&= \lim_{h \rightarrow 0} -\dfrac{8}{(x + h  -4)(x -4)} \\&= -\dfrac{8}{(x+ 0-4)(x – 4)}  \\&= -\dfrac{8}{(x – 4)^2}\end{aligned}

This means that the derivative of $g(x)$ is equal to $-\dfrac{8}{(x – 4)^2}$. We can also write this as $g’(x) = – \dfrac{8}{(x-4)^2}$ or $y’ = – \dfrac{8}{(x-4)^2}$.

Example 2

Find the derivative of $f(x) = \sqrt{x}$ using the definition of derivative.

Solution

If we let $f(x) = \sqrt{x}$, we can find its derivative using the fact that $\dfrac{dy}{dx} = \lim_{h \rightarrow 0} \dfrac{f(x +h) – f(x)}{h}$. We can begin proving the rule by finding the expression for $f(x + h)$ and eventually the quotient difference of the $f(x) = \sqrt{x}$.

\begin{aligned} f(x + h) &= \sqrt{x + h}\\f(x) &= \sqrt{x}\\\\\dfrac{dy}{dx} &= \lim_{h \rightarrow 0} \dfrac{f(x +h) – f(x)}{h}\\&= \lim_{h \rightarrow 0} \dfrac{\sqrt{x + h} – \sqrt{x}}{h} \end{aligned}

What we can do is reverse the process of rationalizing the denominator by multiplying both the numerator and denominator by $\sqrt{x + h} + \sqrt{x}$ then use the algebraic property, $(a- b)(a + b)^2 = a^2 – b^2$.

\begin{aligned} \dfrac{dy}{dx} &= \lim_{h \rightarrow 0} \dfrac{\sqrt{x + h} – \sqrt{x}}{h} \cdot \dfrac{\sqrt{x+h}-\sqrt{x}}{\sqrt{x+h} + \sqrt{x}}\\&= \lim_{h \rightarrow 0}\dfrac{(\sqrt{x+h}-\sqrt{x})(\sqrt{x+h}+\sqrt{x})}{h (\sqrt{x+h} + \sqrt{x})}\\&= \lim_{h \rightarrow 0}\dfrac{(\sqrt{x+h})^2-(\sqrt{x})^2}{h (\sqrt{x+h} + \sqrt{x})}\\&= \lim_{h \rightarrow 0}\dfrac{x+h-x}{h (\sqrt{x+h} + \sqrt{x})} \\&= \lim_{h \rightarrow 0}\dfrac{h}{h (\sqrt{x+h} + \sqrt{x})} \\&= \lim_{h \rightarrow 0}\dfrac{1}{ (\sqrt{x+h} + \sqrt{x})} \end{aligned}

Let’s evaluate the limit of this expression now to find the derivative of $f(x) = \sqrt{x}$.

\begin{aligned} \dfrac{dy}{dx} &= \lim_{h \rightarrow 0}\dfrac{1}{ (\sqrt{x+h} + \sqrt{x})}\\&= \dfrac{1}{\sqrt{x + 0}+\sqrt{x}}\\&= \dfrac{1}{2\sqrt{x}} \end{aligned}

This means that $f’(x) = \dfrac{1}{2\sqrt{x}}$ or $\dfrac{dy}{dx} = \dfrac{1}{2\sqrt{x}}$.

Practice Questions

1. According to the derivative rule for constants, $\dfrac{d}{dx} c = 0$, where $c$ is a constant.
2. Find the derivative of $f(x) = 4x^3 – 2x^2 + 1$ using the definition of derivative.
3. Find the derivative of $g(x) = -4(x -1)^2$ using the definition of derivative.
4. Find the derivative of $h(x) = \dfrac{3x}{x – 9}$ using the definition of derivative.

Answer Key

1.
$\begin{aligned}\dfrac{d}{dx} &= \lim_{h \rightarrow 0} \dfrac{(c + h) – c}{h}\\ &= \lim_{h \rightarrow 0} \dfrac{h}{h}\\ &= \lim_{h \rightarrow 0} 1\\ &= 0\end{aligned}$
2. $f’(x) = 12x^2 – 4x$
3. $g’(x) = 8 – 8x$
4. $h’(x) = -\dfrac{27}{(x – 9)^2} $

Images/mathematical drawings are created with GeoGebra.