Derivative of ln – Derivation, Explanation, and Example

We’ll focus on understanding the derivative of ln in our discussion. The natural logarithmic function helps us quantify and model values that are significantly small or large. With its extensive application in physics and biological sciences, it’s important to know how to differentiate natural logarithmic functions.

The derivative of ln returns the reciprocal of the input value. Whenever possible, the chain rule still applies.

In this article, we’ll learn how to apply the derivative rule for functions that contain $\ln$ in their expression. We’ll also understand how we can use $y = e^x$, its inverse function, to derive the formula for the derivative of $\ln x$.

What is the derivative of ln?    

The derivative of $\ln$ is one of the most remembered derivative rules. That’s because the derivative of $\boldsymbol{\ln x}$ is simply the reciprocal of $\boldsymbol{x}$. Here are two graphs showing us how $y = \ln x$ and $y’ = \dfrac{1}{x}$ would look like on an $xy$-plane.

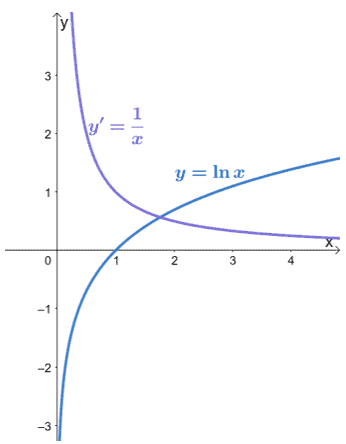
We can extend this rule for composite functions that contain $\ln$ as its outer function.

\begin{aligned}\dfrac{d}{dx}\ln x &= \dfrac{1}{x}\\\dfrac{d}{dx} \ln [g(x)] &= \dfrac{1}{g(x)} \cdot \dfrac{d}{dx} g(x)\\&= \dfrac{g’(x)}{g(x)}\end{aligned}

This means that the chain rule will still apply when we differentiate composite functions that implement the derivative rule for $\ln$.

How to find the derivative of ln and functions containing it?

The derivative of $\ln$ shows us that it’s possible to end up with a rational expression when differentiating functions that are seemingly complex such as $\ln x$. This derivative rule, $\dfrac{d}{dx} \ln x = \dfrac{1}{x}$, will come in handy once we learn how to integrate functions. For now, let’s take a look at how we were able to derive this rule.

What is the derivative of ln x’s proof?

We can begin by applying the rules of logarithms. Recall that we can write $e^{\ln x}$ as $x$. Let’s see what happens when we differentiate both sides of the equations.

\begin{aligned}e^y &= x\\\dfrac{dy}{dx} e^y &= \dfrac{dy}{dx} x\\\dfrac{dy}{dx}e^y &= 1\end{aligned}

Let’s substitute $e^y$ with $x$ to rewrite the equation’s left-hand side in terms of $x$. We can then divide both sides by $x$.

\begin{aligned}e^{\ln x} &= x\\\dfrac{d}{dx} e^{\ln x} &= \dfrac{d}{dx} x\\\dfrac{d}{dx} e^{\ln x} &={\color{Purple} 1}, \color{Purple}\text{Power Rule}\end{aligned}

Recall that $\dfrac{d}{dx} e^x = e^x$, so we can use this to simplify the left-hand side expression. Make sure to apply the chain rule when differentiating $e^{\ln x}$.

\begin{aligned}\dfrac{d}{dx} e^{\ln x} &= 1\\ {\color{Purple}(e^{\ln x})} \cdot {\color{DarkBlue}\dfrac{d}{dx} \ln x} &= 1,\phantom{x}{\color{Purple}\text{Derivative of }e^x}\text{ & }{\color{DarkBlue}\text{Chain Rule}}\end{aligned}

Replace $e^{\ln x}$ with $x$ then divide both sides of the equation by $x$ to isolate $\dfrac{d}{dx} \ln x$ on the left-hand side of the equation.

\begin{aligned}e^{\ln x} \dfrac{d}{dx} \ln x &= 1\\x \dfrac{d}{dx}\ln x &= 1\\\dfrac{d}{dx}\ln x&= \dfrac{1}{x}\end{aligned}

Thus, proving that $\dfrac{d}{dx} \ln x =\dfrac{1}{x}$ is indeed true.  Now that we’ve shown you how to prove this rule let’s see how we can apply this derivative rule to differentiate other functions.

How to use the derivative rule of ln x?

When given a function or a composite function that contains $\ln x$ or $\ln[g(x)]$, we can apply the following process to differentiate the functions:

• Take note of the variable or the inner function.
• Take the reciprocal of the variable or inner function.
• When working with a composite function, make sure to differentiate the inner function.

Let’s say we want to differentiate $y = \ln (x +3)$; we take the reciprocal of $(x + 3)$ and account for the inner function’s derivative through the chain rule.

\begin{aligned}\dfrac{d}{dx} \ln (x +3) &= {\color{Purple}\dfrac{1}{x +3}} \cdot {\color{DarkBlue} \dfrac{d}{dx}(x +3)}, \phantom{x}{\color{Purple}\text{Derivative of ln}}\text{ & }{\color{DarkBlue} \text{Chain Rule}}\\&= \dfrac{1}{x +3}\cdot \left({\color{Purple}\dfrac{d}{dx} x + \dfrac{d}{dx} 3} \right ),\phantom{x}{\color{Purple}\text{Sum Rule}}\\&= \dfrac{1}{x +3}\cdot ({\color{Purple}1}+{\color{DarkBlue}0})\phantom{x}{\color{Purple}\text{Power Rule}}\text{ & }{\color{DarkBlue} \text{Constant Rule}}\\&= \dfrac{1}{x + 3}\end{aligned}

This shows how easy it is for us to differentiate functions with $\ln x$ in their expression or outer function. Of course, the fundamental derivative rules will still apply, so make sure to have a list handy when working on the examples shown below.

Example 1

Find the derivative of the function, $f(x)= 4\ln(2x^2 – 1)$.

Solution

To find $f’(x)$, we can begin by taking $4$ out from the expression that needs to be differentiated. We can then apply the derivative rule, $\dfrac{d}{dx} \ln x = \dfrac{1}{x}$, and the chain rule to differentiate the remaining expression.

\begin{aligned}f'(x) &= \dfrac{d}{dx} 4\ln (2x^2 – 1)\\&= 4\dfrac{d}{dx}\ln (2x^2 -1),\phantom{x}{\color{Purple} \text{Constant Multiple Rule}}\\&= 4 \left({\color{Purple}\dfrac{1}{2x^2 -1}} \right ) \cdot {\color{DarkBlue}\dfrac{d}{dx} (2x^2 – 1)},\phantom{x}{\color{Purple} \text{Derivative of }\ln x}\text{ & }{\color{DarkBlue}\text{Chain Rule}}\end{aligned}

Differentiate $(2x^2 -1)$ using our fundamental derivative rules to further simplify $f’(x)$.

\begin{aligned}f'(x) &= 4 \left(\dfrac{1}{2x^2 -1} \right ) \cdot \left( {\color{Purple}\dfrac{d}{dx} 2x^2 – \dfrac{d}{dx}1}\right),\phantom{x}{\color{Purple} \text{Difference Rule}}\\&= \dfrac{4}{2x^2 -1}\cdot \left( {\color{Purple}2\dfrac{d}{dx} x^2 }- {\color{DarkBlue}0}\right),\phantom{x}{\color{Purple} \text{Constant Multiple Rule}}\text{ & }{\color{DarkBlue}\text{Chain Rule}}\\&= \dfrac{4}{2x^2 -1}\cdot \left( {\color{Purple}2(2x)}\right),\phantom{x}{\color{Purple} \text{Power Rule}}\\&= \dfrac{16x}{2x^2 -1 }\end{aligned}

Hence, we have $f’(x)= \dfrac{16x}{2x^2 -1 }$.

Example 2

Find the derivative of the function, $g(x)= \ln [(x -1)(x + 4)]^4$.

Solution

Before we evaluate $g’(x)$, let’s rewrite the expression using the logarithmic property, $\ln a^n = n \ln a$.

\begin{aligned}g(x) &= 4\ln [(x -1)(x + 4)]\end{aligned}

Differentiate $g(x)$ by using the derivative rule for $\ln x$ and apply the chain rule to account for the derivative of $(x -1)(x +4)$.

\begin{aligned}g'(x) &= \dfrac{d}{dx} 4\ln [(x -1)(x + 4)]\\&= 4\dfrac{d}{dx}\ln [(x -1)(x + 4)],\phantom{x}{\color{Purple}\text{Constant Multiple Rule}}\\&=4\cdot{\color{Purple}\dfrac{1}{(x -1)(x +4)}}\cdot {\color{DarkBlue} \dfrac{d}{dx}(x -1)(x + 4)},\phantom{x}{\color{Purple}\text{Derivative of }\ln x}\text{ & }{\color{DarkBlue}\text{Chain Rule}}\end{aligned}

 Apply the product rule to evaluate $\dfrac{d}{dx} (x -1)(x + 4)$.  Let’s focus on this expression first and go back to $g’(x)$ once we simplify the derivative’s expression.

\begin{aligned} \dfrac{d}{dx}(x -1)(x + 4) &= (x -1)\dfrac{d}{dx} (x +4) + (x+ 4)\dfrac{d}{dx}(x- 1),\phantom{x} {\color{Purple}\text{Product Rule}}\\&= (x -1)\left({\color{Purple}\dfrac{d}{dx} x+\dfrac{d}{dx}4} \right ) + (x+4)\left({\color{Purple}\dfrac{d}{dx} x-\dfrac{d}{dx}1} \right )\phantom{x} {\color{Purple}\text{Sum & Difference Rules}}\\&= (x -1)({\color{Purple}1} + {\color{DarkBlue}0}) +(x +4)({\color{Purple}1} – {\color{DarkBlue}0}),\phantom{x} {\color{Purple}\text{Power Rule}}\text{ & }{\color{DarkBlue}\text{Constant Rule}}\\&= (x -1) + (x + 4)\\&= 2x +3\end{aligned}

Let’s go back to our current expression for $g’(x)$ and substitute the third factor with $2x + 3$.

\begin{aligned}g'(x) &=4\cdot\dfrac{1}{(x -1)(x +4)}\cdot \dfrac{d}{dx}(x -1)(x + 4)\\&=4\cdot\dfrac{1}{(x -1)(x +4)}\cdot (2x +3)\\&= \dfrac{4(2x + 3)}{(x -1)(x +4)}\end{aligned}

This means that $g’(x) = \dfrac{4(2x + 3)}{(x -1)(x +4)}$.

Example 3

The height of a tree after $x$ years since it was planted can be modeled using the function, $h(x) = 8\cdot \ln x$.  What is the rate at which the tree is growing four years after it was planted?

Solution

We can find the growth rate of the tree after four years by evaluating $h’(4)$. We can apply the constant multiple rule and $\dfrac{d}{dx}\ln x=\dfrac{1}{x}$ to find the expression for $h’(x)$.

\begin{aligned}h'(x) &= \dfrac{d}{dx} 8\ln x\\&= 8\dfrac{d}{dx}\ln x,\phantom{x}{\color{Purple}\text{Constant Multiple Rule}}\\&=8\cdot{\color{Purple}\dfrac{1}{x}},\phantom{x}{\color{Purple}\text{Derivative of }\ln x}\\&=\dfrac{8}{x}\end{aligned}

Use this expression to find $h’(4)$. Hence, we have $h’(x) = \dfrac{8}{4} = 2$. This means that the tree’s growth rate is $\boldsymbol{2}$ feet per year.

Practice Questions

1. Find the derivative of the following functions.
a. $f(x) = 6\ln(2x^2 + 5)$
b. $g(x) = -2\ln(4x^3 -2x)$
c. $h(x) = 4\ln(\sqrt{2x})$
2. Find the derivative of the following functions.
a. $f(x) = \ln[(x -1)(x + 2)]^3$
b. $g(x) = -\ln\left(\dfrac{x + 4}{x – 5}\right)$
c. $h(x) = 3\ln(\sqrt{x^2 + 2x +1})$
3. Find the derivative of the following functions.
a. $f(x) = \ln(\cos^2 x)$
b. $g(x) = 3x\ln^2 x$
c. $h(x) = \dfrac{3\ln x}{\sqrt{x^2 + 4}}$

Answer Key

1.
a. $f’(x) = \dfrac{24x}{2x^2 + 5}$
b. $g’(x)= -\dfrac{2\left(6x^2 – 1\right)}{x\left(2x^2 – 1\right)}$
c. $h’(x) = \dfrac{2}{x}$
2.
a. $f’(x) = \dfrac{3\left(2x + 1\right)}{\left(x – 1\right)\left(x + 2\right)}$
b. $g’(x)= \dfrac{9}{\left(x+4\right)\left(x-5\right)}$
c. $h’(x) = \dfrac{3}{x + 1}$
3.
a. $f’(x) = -2 \tan x$
b. $g’(x) = 3(\ln^2 x+ 2\ln x)$
c. $h’(x) = \dfrac{3\left[x^2 + 4 – x^2 \ln \left(x\right)\right]}{x\left(x^2 + 4\right)\sqrt{x^2 + 4}}$

Images/mathematical drawings are created with GeoGebra.