Diagonal Matrix – Explanation & Examples

A diagonal matrix is a square matrix whose elements, other than the diagonal, are zero. There are certain conditions that must be met for a matrix to be called a diagonal matrix. Firstly, let’s check the formal definition of a diagonal matrix.

A square matrix in which all the elements except the principal diagonal are zero is known as a diagonal matrix.

In this article, we are going to take a close look at what makes a matrix diagonal, how to find diagonal matrices, properties of diagonal matrices, and the determinant of a diagonal matrix. Let’s start!

What is a Diagonal Matrix?

A matrix to be classified as a diagonal matrix, it has to meet the following conditions:

• square matrix
• all elements (entries) of the matrix, other than the principal diagonal, has to be $ 0 $

A square matrix is said to be:

• lower triangular if its elements above the principal diagonal are all $ 0 $
• upper triangular if its elements below the principal diagonal are all $ 0 $

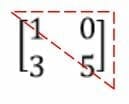
Lower Triangular Matrix

Upper Triangular Matrix

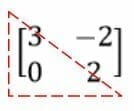
A diagonal matrix is a special square matrix that is BOTH upper and lower triangular since all elements, whether above or below the principal diagonal, are $ 0 $.

How to find Diagonal Matrix

To find, or identify, a diagonal matrix, we need to see if it is a square matrix and all the elements besides the principal diagonal (diagonal that runs from top left to bottom right) are $ 0 $. Let’s take a look at the matrices shown below:

$ A = \begin{pmatrix} 3 & 0  \\ 0 & { – 3 } \end {pmatrix} $

$ B = \begin{pmatrix} 1 & 0 & 0  \\ 0 & 5 & 0 \\ 0 & 0 & { – 2 } \end {pmatrix} $

$ C = \begin{bmatrix} 10 & 0  \\ 0 & 12 \\ 0 & 12  \end {bmatrix} $

$ D = \begin{bmatrix} { – 5 } & 0 & 0  \\ 0 & 0 & 0 \\ 0 & 0 & { 9 } \end {bmatrix} $

Note the following observations about each of the $ 4 $ matrices shown above:

• Matrix $ A $ is a square matrix because its has the same number of rows and columns ($ 2 \times 2 $ matrix). The principal diagonal has entries $ 3 $ and $ -3 $, respectively. All other entries are $ 0 $. Thus, this is a diagonal matrix.
• Matrix $ B $ is a square matrix because its has the same number of rows and columns ($ 3 \times 3 $ matrix). The principal diagonal has entries $ 1 $, $ 5 $, and $ -2 $, respectively. All other entries are $ 0 $. Thus, this is a diagonal matrix.
• A false glance at Matrix $ C $ will make us think that it is a diagonal matrix. But, first and foremost, it is not a square matrix. Hence, it cannot be a diagonal matrix.
• This one’s a bit tricky. First of all, it is in fact a square matrix ( $ 3 \times 3 $ ). You will think that it is not a diagonal matrix.But why? Is it because there’s a $ 0 $ in the middle?
  

  If you take a closer look at the definition of a diagonal matrix, you will see that nowhere does it say that the entries in the diagonal cannot be $ 0 $! The condition is that the elements other than the diagonal has to be $ 0 $. So, even if there are elements that are $ 0 $ in the diagonal, it won’t matter. As long as the elements besides the diagonal are $ 0 $, it will be a diagonal matrix.

  Thus, Matrix $ D $ is in fact a diagonal matrix!

This brings us to $ 2 $ special types of diagonal matrices:

• Identity Matrix
• Zero Matrix

Identity Matrix

This is a square matrix in which all the entries in the principal diagonal are $ 1 $ and all other elements are $ 0 $. A $ 2 \times 2 $ and a $ 3 \times 3 $ identity matrices are shown below.

$ 2 \times 2 $ identity matrix

$ \begin{bmatrix} 1 & 0 \\ 0 & 1 \end {bmatrix} $

$ 3 \times 3 $ identity matrix

$ \begin{bmatrix} 1 & 0 & 0  \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end {bmatrix} $

You can read more about identity matrices here.

Zero Matrix

A matrix in which all the elements are $ 0 $.  A $ 2 \times 2 $ and a $ 3 \times 3 $ zero matrices are shown below.

$ 2 \times 2 $ zero matrix

$ \begin{bmatrix} 0 & 0 \\ 0 & 0 \end {bmatrix} $

$ 3 \times 3 $ zero matrix

$ \begin{bmatrix} 0 & 0 & 0  \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end {bmatrix} $

Now, let’s look at some properties of diagonal matrices.

Properties of Diagonal Matrices

There are several properties of diagonal matrices but for the purpose of this article, we will look at $ 3 $ properties of diagonal matrices. Below, we take a look at the properties and their examples.

Property 1:

When $ 2 $ diagonal matrices of the same order are added or multiplied together, the resultant matrix is another diagonal matrix with the same order.

Consider the matrices shown below:

$ A = \begin{bmatrix} 3 & 0 \\ 0 & 4 \end {bmatrix} $
$ B = \begin{bmatrix} 1 & 0 \\ 0 & 5 \end {bmatrix} $

Now, we add both the $ 2 \times 2$ matrices and show that the resultant matrix is also diagonal.

$ A + B = \begin{bmatrix} 3+1 & 0+0 \\ 0+0 & 4+5 \end {bmatrix} $

$ A + B = \begin{bmatrix} 4 & 0 \\ 0 & 9 \end {bmatrix} $

Thus, we see that the resultant matrix, $A + B$, is also a diagonal matrix of the order $2 \times 2$.

Let’s check matrix multiplication with the same matrices. We multiply Matrix $A$ and Matrix $B$ and show that the resultant is also a diagonal matrix with the same order. Shown below:

$ A \times B = \begin{bmatrix} 3 & 0 \\ 0 & 4 \end {bmatrix} \times \begin{bmatrix} 1 & 0 \\ 0 & 5 \end {bmatrix}  $

$ A \times B = \begin{bmatrix} {3\times1+0\times0} & 3\times 0 + 0 \times 5 \\ 0 \times 1 + 4 \times 0 & 0\times0 + 4 \times 5 \end {bmatrix} $

$ A \times B = \begin{bmatrix} 3 & 0 \\ 0 & 20 \end{bmatrix} $

Thus, we see that the resultant matrix, $A \times B$, is also a diagonal matrix of the order $2 \times 2$.

To learn more about how we did matrix multiplication, please have a look at the article here.

Property 2:

The transpose of a diagonal matrix is the matrix itself.

If we have a matrix $A$, then we denote its transpose as $A^{T}$. Transposing a matrix means to flip its rows and columns. Let’s show that this property is true by calculating the transpose of Matrix $A$.

$ A = \begin{bmatrix} 3 & 0 \\ 0 & 4 \end {bmatrix} $

$ A^{T} = \begin{bmatrix} 3 & 0 \\ 0 & 4 \end {bmatrix} $

Interchanging the rows and columns produces the same matrix because of the entries besides the diagonal being $0$.

Property 3:

Under multiplication, diagonal matrices are commutative. 

If we have $2$ matrices, $A$ and $B$, this means $AB = BA$. Let’s show this property by using the two matrices from above.

$ A \times B = \begin{bmatrix} {3\times1+0\times0} & 3\times 0 + 0 \times 5 \\ 0 \times 1 + 4 \times 0 & 0\times0 + 4 \times 5 \end {bmatrix} $

$ A \times B = \begin{bmatrix} 3 & 0 \\ 0 & 20 \end{bmatrix} $

Now,

$ B \times A = \begin{bmatrix} {1\times3+0\times0} & 1\times 0 + 0 \times 4 \\ 0 \times 3 + 5 \times 0 & 0\times0 + 5 \times 4 \end {bmatrix} $

$ B \times A = \begin{bmatrix} 3 & 0 \\ 0 & 20 \end{bmatrix} $

Thus, we have seen that $AB = BA$.

Determinant of Diagonal Matrix

First, let’s look at the determinant of a $2\times2$ matrix.

Consider Matrix $M$ shown below:

$ M = \begin{pmatrix} a & b \\ c & d  \end{pmatrix} $

The determinant of this matrix is:

$ det(M) = ad – bc $

One property of a diagonal matrix is that the determinant of a diagonal matrix is equal to the product of the elements in its principal diagonal.

Let’s see if it’s true by finding the determinant of the diagonal matrix shown below.

$ N = \begin{pmatrix} 2 & 0 \\ 0 & 8  \end{pmatrix} $

$ det(N) = (2\times8)-(0\times0) = 16 $

This is in fact the product of the elements in its diagonal, $2\times8=16$.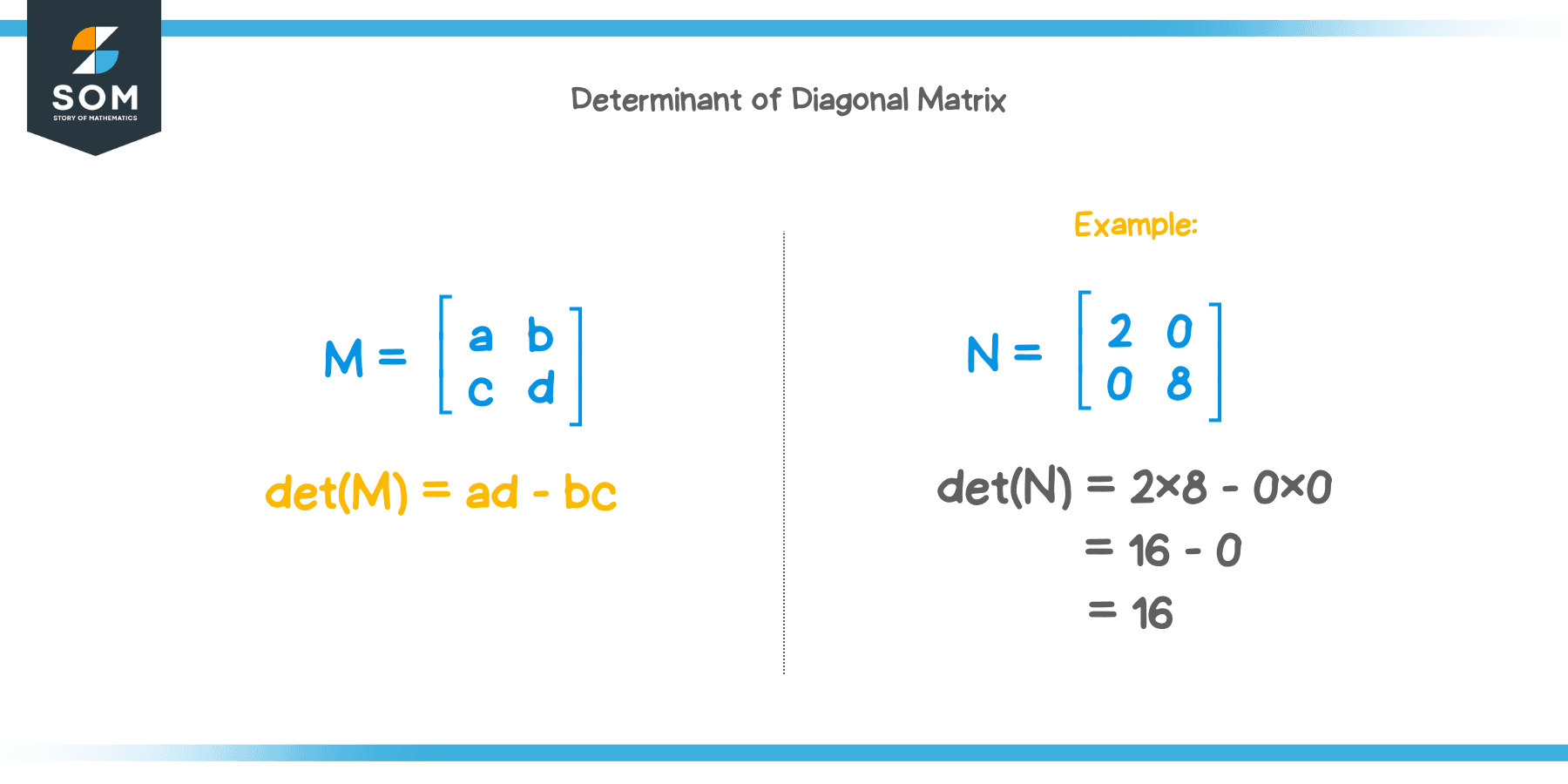

Example 1

For the matrices shown below, identify whether they are diagonal matrix or not.

$ A = \begin{bmatrix} {-2} & 0 \\ 0 & {-7} \end {bmatrix} $

$ B = \begin{bmatrix} a & 0 \\ 0 & b \\ 0 & d \end {bmatrix} $

$ C = \begin{bmatrix} 3 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 11 \end {bmatrix} $

$ D = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end {bmatrix} $

Solution

• Matrix A is a $2\times2$ matrix with the elements being 0 other than the diagonal. So, this is a diagonal matrix.
• Matrix B is a $3\times2$ matrix. It’s not square, so immediately we can say that it is not a diagonal matrix.
• Matrix C is a square matrix ($3\times3$). Also all the elements besides the diagonal are $0$. So, it is a diagonal matrix. Moreover, an entry of the diagonal is also $0$, it doesn’t matter as long as all the entries except the diagonal are zeros.
• Matrix D is a special type of diagonal matrix. It is a zero matrix. Therefore, it is a diagonal matrix.

Example 2

Will multiplying Matrix A and Matrix B result in a diagonal matrix?

$ A = \begin{bmatrix} {-9} & 0 \\ 0 & 0 \end {bmatrix} $

$ B = \begin{bmatrix} 1 & 0 \\ 1 & 1 \end {bmatrix} $

Solution

Matrix A is a diagonal matrix but Matrix B is not. So, multiplying  Matrix A and B will not result in a diagonal matrix.

Example 3

Find the determinant of the matrix shown below:

$ B = \begin{bmatrix} 8 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & {-1} \end {bmatrix} $

Solution

Matrix B is a $3\times3$ diagonal matrix. Recall that the product of all the entries of the diagonal of a diagonal matrix is its determinant. Thus, we simply multiply and find the answer:

$ det(B) = 8 \times 4 \times {-1} = – 32$

Practice Questions

1. Identify which of the following matrices are diagonal matrices.
   $ J = \begin{pmatrix} 0 & 0 \\ 0 & {-5} \end{pmatrix} $
   $ K = \begin{pmatrix} 0 & 2 \\ 1 & {-1} \end{pmatrix} $
   $ L = \begin{bmatrix} -3 & 0 & 0 \\ 0 & {-5} & 0 \\ 0 & 0 & 3 \end{bmatrix} $
2. Calculate the determinant of the matrix shown below:
   $ T = \begin{bmatrix} -1 & 0 & 0 \\ 0 & {-1} & 0 \\ 0 & 0 & 4 \end{bmatrix} $
3. Given
   $ A = \begin{pmatrix} 2 & 0 \\ 0 & {-1} \end{pmatrix} $
   $ B = \begin{pmatrix} 1 & 0 \\ 1 & {-2} \end{pmatrix} $

   Is $AB = BA$ ?

Answers

1. Matrix J is a square matrix. All the elements other than the principal diagonal are zeros. This is a diagonal matrix.
   Matrix K is a square matrix but not all the elements, except the diagonal, are zero. Thus, this is not a diagonal matrix. 
   Matrix L is a square matrix (3\times3). The elements other than the diagonal entries are zero. So, this is a diagonal matrix.
2. This is a diagonal matrix. We can find the determinant of this matrix by taking the product of all the 3 entries of the diagonal. Thus, the determinant is:
   $ det(T) = -1 \times -1 \times 4 = 4 $
3. If two matrices are diagonal, the multiplication of those two matrices are commutative. Looking at Matrix A and B, we can see that Matrix A is diagonal but Matrix B is not. Hence, their multiplication will not be commutative.

   Thus, $ AB \neq BA$.

Previous Lesson | Main Page | Next Lesson