- Home
- >
- Dimension of a matrix – Explanation & Examples
JUMP TO TOPIC
Dimension of a Matrix – Explanation & Examples
 Matrices are a rectangular arrangement of numbers in rows and columns. They are sometimes referred to as arrays. The dimensions of a matrix are basically its name. Knowing the dimension of a matrix allows us to do basic operations on them such as addition, subtraction and multiplication. Let’s start with the definition of the dimension of a matrix:
Matrices are a rectangular arrangement of numbers in rows and columns. They are sometimes referred to as arrays. The dimensions of a matrix are basically its name. Knowing the dimension of a matrix allows us to do basic operations on them such as addition, subtraction and multiplication. Let’s start with the definition of the dimension of a matrix:
The dimension of a matrix is its number of rows and columns.
This article will talk about the dimension of a matrix, how to find the dimension of a matrix, and review some examples of dimensions of a matrix. If you want to know more about matrix, please take a look at this article.
What is the dimension of a matrix?
The dimension of a matrix is the number of rows and the number of columns of a matrix, in that order. Consider the matrix shown below:

It has $ 2 $ rows (horizontal) and $ 2 $ columns (vertical). The dimension of this matrix is $ 2 \times 2 $. The first number is the number of rows and the next number is the number of columns. It has to be in that order. We pronounce it as a “2 by 2 matrix”. The $ \times $ sign is pronounced as “by”.
The entries, $ 2, 3, -1 $ and $ 0 $, are known as the elements of a matrix.
In general, if we have a matrix with $ m $ rows and $ n $ columns, we name it $ m \times n $, or rows x columns. The convention of rows first and columns second must be followed. This is the dimension of a matrix. You can remember the naming of a matrix using a quick mnemonic.
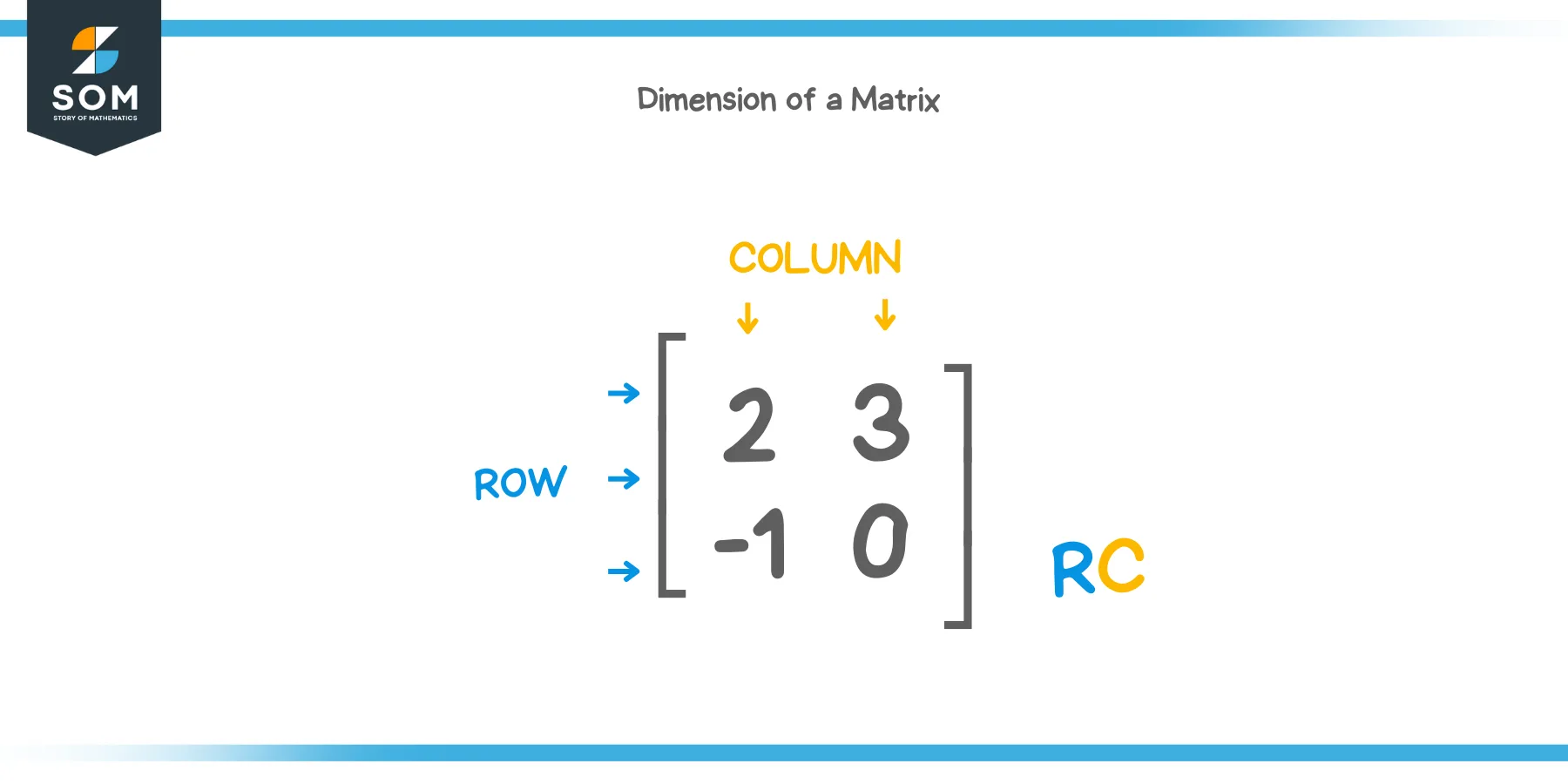 Remember, RC. Rows first, then columns.
Remember, RC. Rows first, then columns.
How to find the dimension of a matrix?
To find the dimension of a given matrix, we count the number of rows it has. Then, we count the number of columns it has. We put the numbers in that order with a $ \times $ sign in between them. Let’s take an example.
How many rows and columns does the matrix below have?
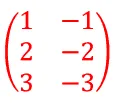
Checking horizontally, there are $ 3 $ rows. Checking vertically, there are $ 2 $ columns. Thus, we have found the dimension of this matrix. It is a $ 3 \times 2 $ matrix.
What about this matrix?

This can be a bit tricky. But if you always focus on counting only rows first and then only columns, you won’t encounter any problem. We see there are only $ 1 $ row (horizontal) and $ 2 $ columns (vertical). Thus, this matrix will have a dimension of $ 1 \times 2 $.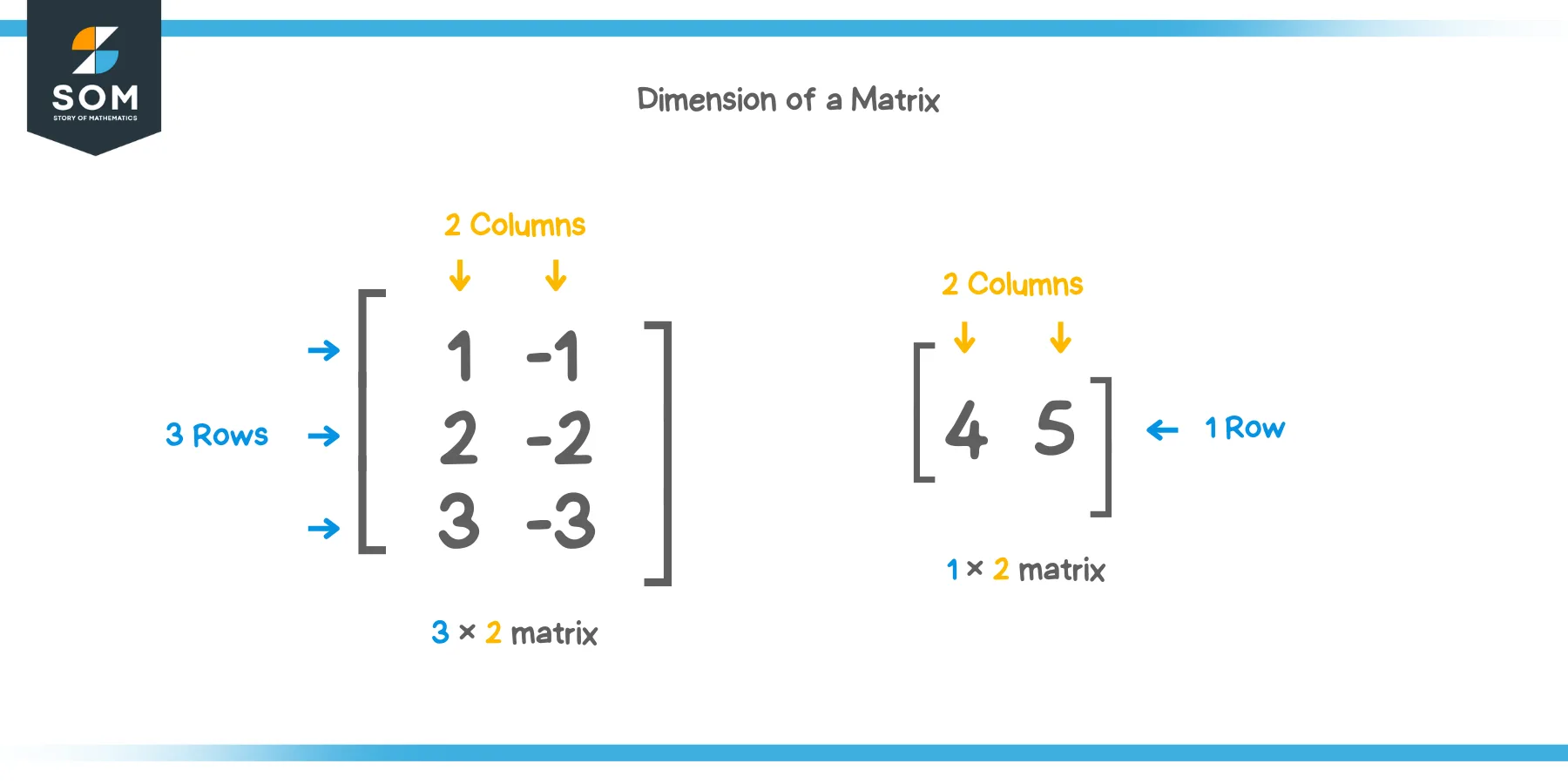
Let us look at some examples to enhance our understanding of the dimensions of matrices.
Example 1
What is the dimension of the matrix shown below?
$ \begin{pmatrix} 1 & { 0 } & 1 \\ 1 & 1 & 1 \\ 4 & 3 & 2 \end{pmatrix} $
Solution
Recall that the dimension of a matrix is the number of rows and the number of columns a matrix has, in that order. Always remember to think horizontally first (to get the number of rows) and then think vertically (to get the number of columns).
Looking at the matrix above, we can see that is has $ 3 $ rows and $ 3 $ columns. Therefore, the dimension of this matrix is $ 3 \times 3 $.
Let us look at another example.
Example 2
What is the dimension of the matrix shown below?
$ \begin{pmatrix} a \\ b \\ c \end{pmatrix} $
Solution
This is a small matrix. You should be careful when finding the dimensions of these types of matrices. Check horizontally, you will see that there are $ 3 $ rows. Check vertically, there is only $ 1 $ column. From the convention of writing the dimension of a matrix as rows x columns, we can say that this matrix is a $ 3 \times 1 $ matrix.
Please note that the elements of a matrix, whether they are numbers or variables (letters), does not affect the dimensions of a matrix. The dimension only depends on the number of rows and the number of columns. You can have number or letter as the elements in a matrix based on your need.
We now see a tricky problem.
Example 3
What is the dimension of the matrix shown below?
$ \begin{bmatrix} { 5 } \end{bmatrix} $
Solution
At first glance, it looks like just a number inside a parenthesis. Well, this can be a matrix as well. We have a single entry in this matrix. The number of rows and columns are both one. Thus, this is a $ 1 \times 1 $ matrix.
Practice Questions
- What are the individual entries in a matrix called?
- True or False
A matrix has $ 5 $ rows and $ 2 $ columns. The dimension of the matrix is $ 2 \times 5 $. - What is the dimension of this matrix?
$ \begin{bmatrix} a & b & c \\ f & e & d \end{bmatrix} $ - Does the matrix shown below have a dimension of $ 1 \times 5 $?
$ \begin{pmatrix} 22 \\ 3 \\ { – 2 } \\ 5 \\ 1 \end{pmatrix} $
Answers
- The individual entries in any matrix are known as elements. They can be either numbers or variables.
- When naming a matrix, i.e. the dimension of a matrix, we always put the number of rows first. Then a $ \times $ sign, followed by the number of columns. Since there are $ 5 $ rows and $ 2 $ columns, the dimension of the matrix should be $ 5 \times 2 $. Hence, the statement is False.
- If there are m rows and n columns of a matrix, the dimension of that matrix is $ m \times n $. From the matrix shown, we see that there are $ 2 $ rows and $ 3 $ columns. Thus, the dimension of this matrix is $ 2 \times 3 $.
- If there are m rows and n columns of a matrix, the dimension of that matrix is $ m \times n $. Looking at the matrix, we can see that it has $ 5 $ rows and $ 1 $ column. Hence, its dimension is $ 5 \times 1 $. So, NO, the matrix DOES NOT have dimension of $ 1 \times 5 $.
