Dividing Numbers in Scientific Notation – Methods & Examples

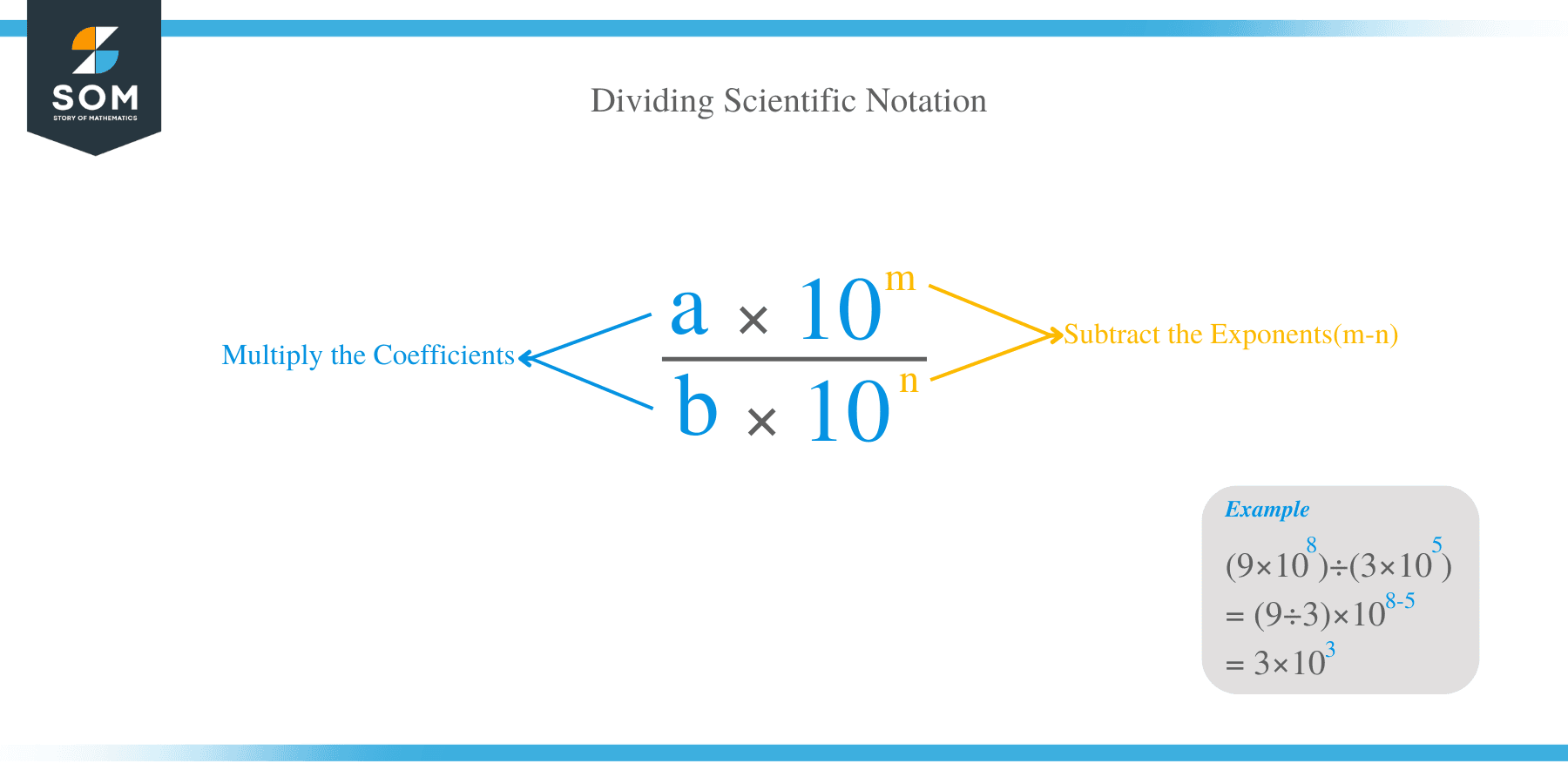
Scientific notation is a method of writing numbers in the form of a x 10^b   where 1 ≤ a < 10. The number ‘a’ is referred to as the coefficient while ‘b’ is the power or exponent.

This type of notation is easier and more concise to express quantities that are too big or small. For example, the number 125,000,000,000 can be represented as 1.25 x 10 ¹¹.

How to Divide Scientific Notation?

This article illustrates how you can perform division of numbers expressed in scientific notation.

To divide two numbers written in scientific notation, follow the steps below:

• Separately divide the coefficients and exponents.
• For the division of bases, use the division rule of exponents, where the exponents are subtracted.
• Combine the result of coefficients by the new power of 10.
• If the quotient from division of coefficients is not less than 10 and greater than 1, convert it to scientific notation and multiply it by the new power of 10.
• Note that when you dividing exponential terms, always subtract the denominator from the numerator.

Let us take a look at a few examples to help you understand the above procedures better.

Example 1

Divide and express the answer in scientific notation: 9 x 10 ⁸/ 3 x 10 ⁵.

Explanation

• Start by dividing the coefficients: (9 ÷ 3) = 3
• Now, divide the bases using the division rule of exponents: (10 ⁸ ÷ 10 ⁵) = 10 ^{8 – 5}=10 ³
• The coefficient is less than 10 and greater than 1, therefore multiply it by the new power of 10.
• And thus, the answer is 3 x 10 ³

Example 2

(2.8 x 10¹⁰) / (2 x 10 ²⁰)

Solution

Divide the coefficients and bases separately:

= (2.8/2) x (10¹⁰/10²⁰)

= 1.4 x 10^{10- 20}

= 1.4 x 10 ^-10

Example 3

(6.4 x 10⁶)/ (8.9 x 10²)

Solution

Divide the coefficients and powers of 10 separately;

= (6.4)/ (8.9) x 10^(6-2)

= 0.719 x 10⁴
The new coefficient is less than 1, therefore convert the number to scientific notation and multiply by the power of 10.

= 7.19 x 10³

Example 4

(3.2 x 10³)/ (5.7 x 10^–2)

Solution

Divide the coefficients and bases separately

= (3.2)/ (5.7) x 10^3–(–2)

= 0.561 x 10⁵

The coefficient is less than 1, therefore convert the number to scientific notation by moving the decimal point one step to the right.

= 5.61 x 10⁴

Example 4

(2 x 10 ³) / (4 x 10^-8)

Solution

Divide the coefficients and bases separately:

= (2/4) x (10³/10^-8)

= 0.5 x 10 ^{3 – (-8)}

= 0.5 x 10 ¹¹

Since the new coefficient is less than 1; convert it to scientific notation:

= 0.5 = 5 x 10 ^-1

Now multiply the coefficient by the new power of 10;

= (5 x 10 ^-1) x (10 ¹¹)

= 5 x 10 ¹⁰

Example 5

Evaluate and express your answer in scientific notation:

(2.688 x 10⁶) / (1.2 x 10²)

Solution

= (2.688 / 1.2) x (10⁶ / 10²)

= (2.24) x (10^6-2)

= 2.24 x 10⁴