• Home
  • >
  • Division – Explanation & Examples

Division – Explanation & Examples

What is DivisionDivision is one of the four basic operations which distributes a number into equal parts. It is denoted by several symbols: the slash, the horizontal line, and the division sign. The horizontal line was introduced by Arabs and used by European mathematicians in the 13th century. It was officially first used by a Swedish mathematician, Johann Rahn, in 1659.

What is Division?

The division is a mathematical technique where a number is shared into smaller groups or a technique of distributing quantities into equal parts. It is normally one of the basic operations in arithmetic, which results in fair sharing.

The division is an inverse operation of multiplication. For example, the multiplication of 5 by 2 gives 10. Either of the factors 2 and 5 can be obtained by dividing 10 by any of the numbers.

Parts of Division

  • The Dividend

In the division sentence, the dividend is the number that is to be divided. For example, in an expression: 12 ÷ 3 = 4 1/3, the dividend is the number 12.

  • The Divisor

The divisor in the division sentence is the number that divides the dividend. For instance, in an equation: 12 ÷ 3 = 4 1/3, the number 3 is the divisor.

  • The Quotient

The quotient is the number of times the divisor divides the dividend. In this 12 ÷ 3 = 4 1/3, 4 is the quotient.

  • The Remainder

The number which is left over after the operation of division is known as the remainder. For example, in 12 ÷ 3 = 4 1/3, the number 1 is the remainder. It can be noted that the divisor is the denominator of the answer.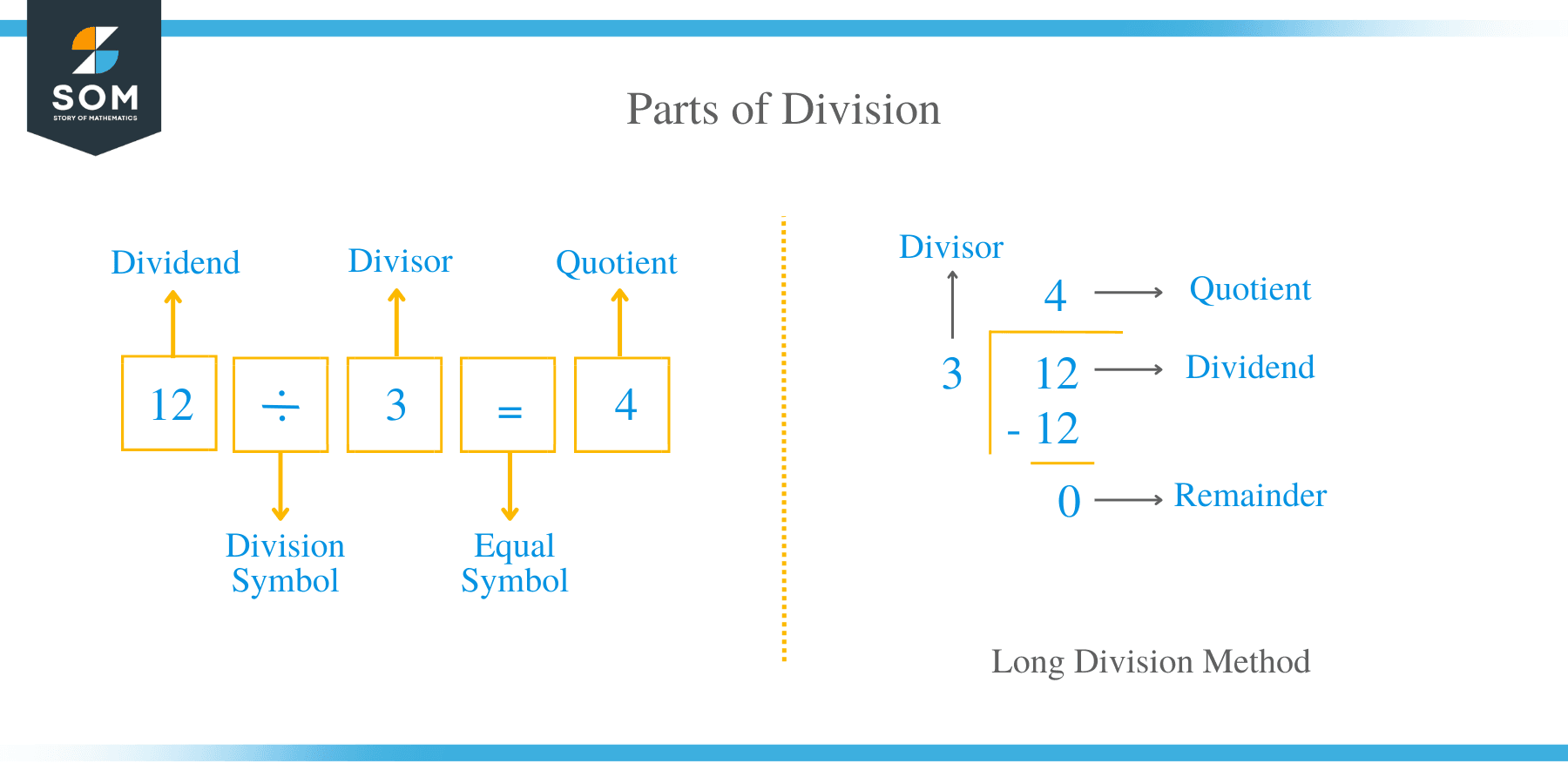Parts of Division

Properties of Division

  • Closure Property

In division, the closure property states that the division of two whole numbers does not give a quotient a whole number. For example, in 10 ÷ 5, the quotient is a whole number, but for 5 ÷ 10, the quotient is not a whole number.

  • Commutative Property

The commutative property does not apply to the division of numbers. For instance, a ÷ b ≠ b ÷ a.

  • Associative Property

The Associative property does not apply to the division of numbers. In general, a ÷ (b ÷ c) ≠ (a ÷ b) ÷ c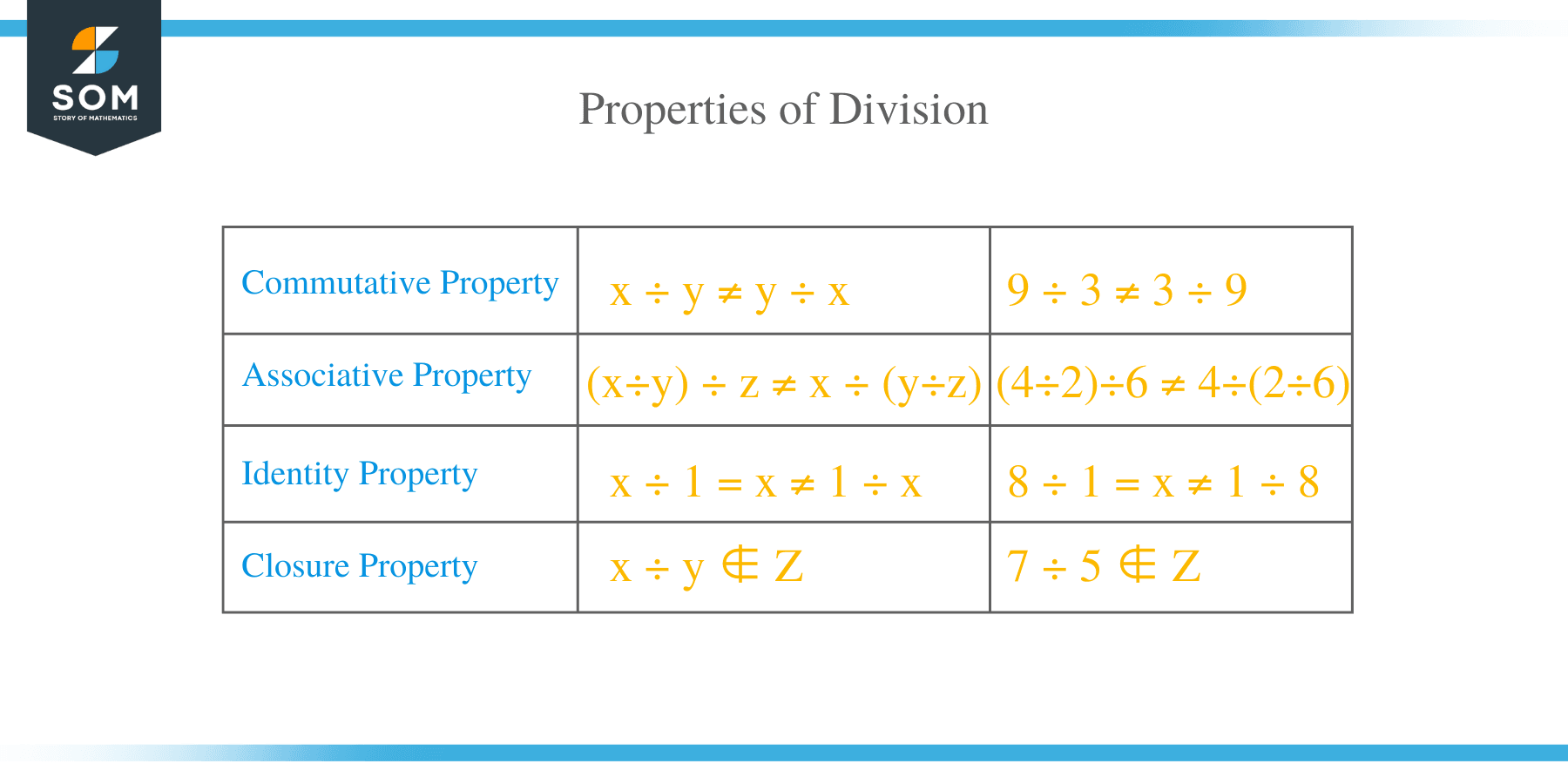Properties of Division

How to Divide Numbers?

  • When a number is divided by 1, the quotient is the number itself.

Example: 45 ÷ 1= 45.

  • The quotient is 1 if a number is divided by itself.

Example: 5 ÷ 5 = 1

  • In the division of any negative or positive number by zero, the result is always undefined. It is therefore meaningless to divide any number by 0.

Example: 2 ÷ 0 = Undefined

  • The division of zero by any positive or negative number gives zero as the quotient.

Example: 0 ÷ 2 = 0

  • The decimal point is moved to the left in the division of any number by another number in multiples of 10, 100, 1000, etc.

Example: 5 ÷ 10 = 0.5 and 5 ÷ 1000 = 0.005

  • Positive number / Positive number =  Positive quotient

Negative number / Negative number =  Positive quotient

Negative number / Positive number  =  Negative quotient

Positive number / Negative number  =  Negative quotient

Practice Questions

1. A total of $\$5,876$ was shared among $26$ workers. How much money did each person get if the money was shared equally?

2. A total of $9975$ kg of rice is to be packed into $95$ bags. How many kilograms will each bag weigh?

3. There are $89$ people invited at a party, and one table can serve only $12$ people. How many tables are needed at the party?

4. How many hours are there in $1200$ minutes?

5. A bus has a capacity of $108$ passengers. If the bus has $12$ rows of seats, how many seats per row are there on the bus?

6. A woman had $63$ oranges in a basket. If she equally distributed all the oranges amongst her $9$ daughters. How many did each one of them receive?

7. A shopkeeper repackaged $195$ cakes into $13$ packs. How many cakes did he include in each pack?

8. Five mangoes are needed to make one glass of mango juice. How many glasses of mango juice can be made from $250$ mangoes?


 

Previous Lesson | Main Page | Next Lesson