The Division Property of Equality – Explanation and Examples

The division property of equality states that dividing two equal terms by a common, non-zero value retains the equality.

The division property of equality follows from the multiplication property of equality. It is useful in both arithmetic and algebra.

Before reading this section, make sure to review the properties of equality.

This section covers:

• What Is Division Property of Equality?
• Division Property of Equality Definition
• Converse of the Division Property of Equality
• Uses for the Division Property of Equality
• Is the Division Property of Equality an Axiom?
• Division Property of Equality Example

What Is Division Property of Equality?

The division property of equality states that two terms are still equal when dividing both sides by a common term.

It is similar to some of the other operational properties of equality. These include the addition, subtraction, and multiplication properties.

The division property, however, stands out. This is because it requires the third number to be any real number except zero. All of the other properties hold for any real number, even $0$.

Division Property of Equality Definition

If equals be divided by non-zero equals, the quotients are equal.

In other words, dividing two equal terms by a third term means the quotients are equal as long as the third term is not equal to zero.

Arithmetically, let $a, b,$ and $c$ be real numbers such that $a=b$ and $c$. Then:

$\frac{a}{c}= \frac{b}{c}$

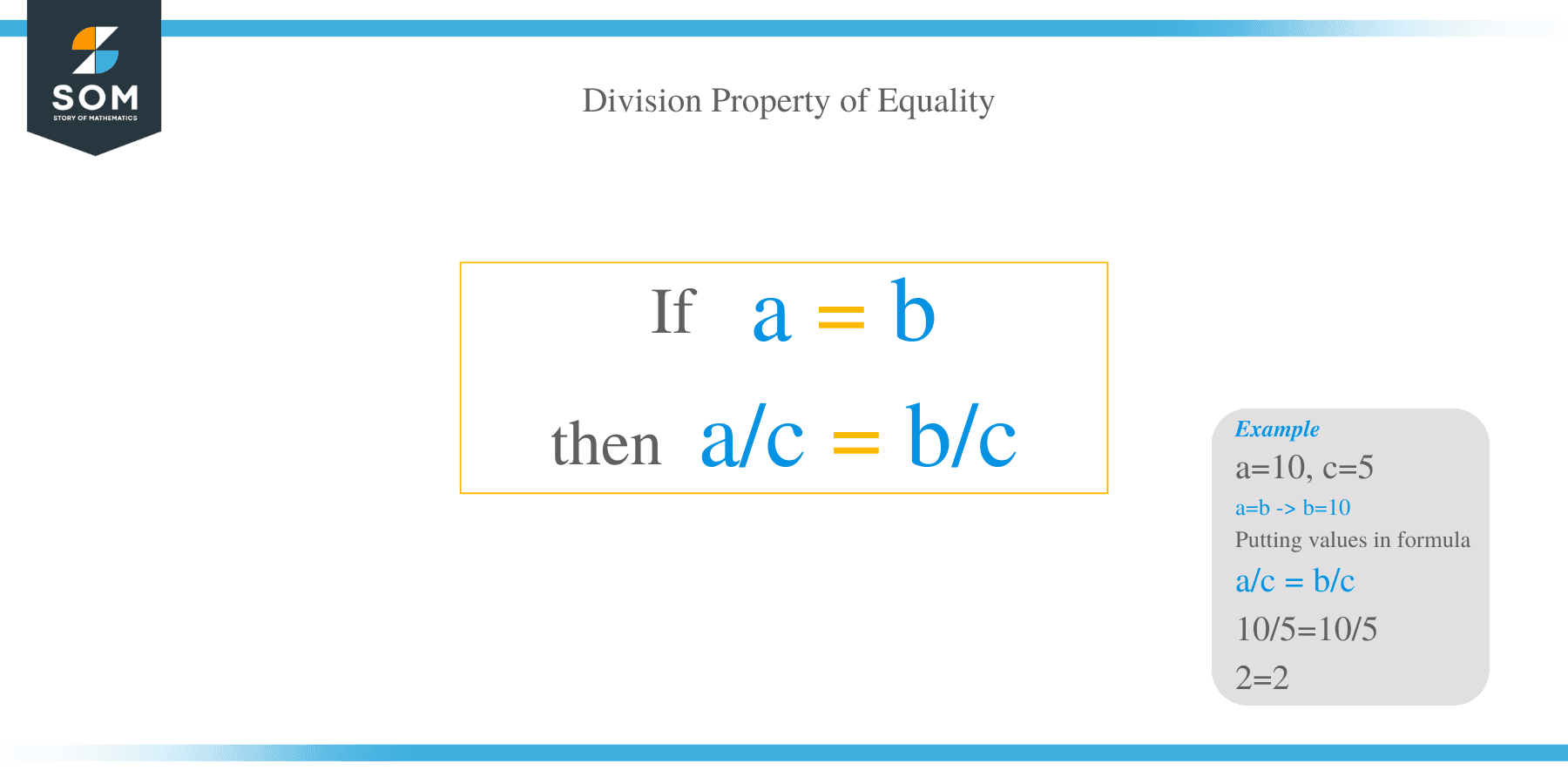
Converse of the Division Property of Equality

The converse of the division property of equality is also true. That is, let $a, b, c$ be real numbers such that $a\neq b$ and $c\neq0$. Then $\frac{a}{c}\neq \frac{b}{c}$.

Put another way, let $a, b, c,$ and $d$ be real numbers such that $a=b$, $c\neq0$, and $d\neq0$. Then $\frac{a}{c}= \frac{b}{d}$, then $c=d$.

Uses for the Division Property of Equality

Like the other similar properties of equality, the division property of equality has uses in both arithmetic and algebra.

In arithmetic, the division property of equality helps to decide whether two math terms are equal.

In algebra, the division property of equality justifies steps when solving for an unknown value. Doing this requires getting a variable by itself. Division will undo any multiplication done to a variable.

Is the Division Property of Equality an Axiom?

The division property of equality derives from the multiplication property of equality. Thus, axiom lists do not need to have it. However, most lists of them do.

Euclid did not define the division property of equality or the multiplication property of equality in his Elements. This is notable since he did define several others. The most likely reason for this is that neither property has many uses in the planar geometry he was working on.

Giuseppe Peano made his list of arithmetic axioms in the 1800s. He did not directly include the division property of equality. This list was meant to make sure mathematical rigor when logic-based math was taking off. However, his axioms are usually augmented with addition and multiplication. Division follows from these.

Thus, even though the division property of equality is deducible from other axioms, it is often listed as an axiom in its own right. It has a lot of uses, so this makes reference easy.

Note, however, that is is possible to deduce the multiplication property of equality from the division property of equality. Example 3 does just that.

Division Property of Equality Example

Like the multiplication property of equality, Euclid did not define the division property of equality in his Elements. As a result, there are not any famous geometric proofs that rely on it.

There is a famous example of the necessity of the statement that $c\neq0$ though. Skipping this requirement can lead to logical errors. This is shown in the example below.

Let $a$ and $b$ be real numbers such that $a=b$.

Then:

1. $a^2=ab$ by the multiplication property.
2. $a^2-^2=ab-b^2$ by the subtraction property.
3. $(a+b)(a-b)=b(a-b)$ by the distributive property.
4. $(a+b)=b$ by the division property.
5. $2b=b$ by the substitution property.
6. $2=1$ by the division property.

$2\neq1$. Clearly, there is some mistake in this logic.

The problem was in step 4. Here, $a-b$ divides both sides. But, since $a=b$, the substitution property states that $a-b=a-a=0$.

Dividing by $0$ in step 4 was the logical flaw.

Examples

This section covers common examples of problems involving division property of equality and their step-by-step solutions.

Example 1

Let $a, b, c,$ and $d$ be real numbers such that $a=b$ and $c=d$. Assume $a\neq0$ and $c\neq0$. Use the division property of equality to determine which of the following are equivalent.

• $\frac{a}{c}$ and $\frac{b}{c}$
• $\frac{a}{c+d}$ and $\frac{b}{c+d}$
• $\frac{a}{c-d}$ and $\frac{b}{c-d}$

Solution

The first two pairs are equivalent, but the third pair is not.

Recall that $c$ is not equal to $0$ and $a$ is equal to $b$. The division property of equality says that $\frac{a}{c}$ and $\frac{b}{c}$ must be equal.

$c\neq0$, but $c$ is equal to $d$. If $c+d=0$, the substitution property of equality states that $c+c$ is also equal to $0$. This simplifies to $2c=0$. The multiplication property then states that $c=0$.

Therefore, since $c \neq0$, $c+d$ is not equal to $0$ either. Therefore, according to the division property of equality, $\frac{a}{c+d}$ and $\frac{b}{c+d}$.

However, since $c=d$, the substitution property of equality says that $c-d=c-c$. Since $c-c=0$, $c-d=0$ by the transitive property.

Thus, dividing by $c-d$ is the same as dividing by $0$. Therefore, equality does not hold and $\frac{a}{c-d}$ and $\frac{b}{c-d}$ are not equal.

Example 2

Two small local libraries have the same number of books. Each library divides its books evenly among 20 shelves. How do the number of books on each shelf at the first small library compare to the number of books on the each shelf at the second small library.

Solution

Let $f$ be the number of books at the first library and let $s$ be the number of books at the second library. It is given that $f=s$.

The first library divides all of its books evenly among 20 shelves. This means that each shelf has $\frac{f}{20}$ books.

The second one also divides all of its books evenly among 20 shelves. This means that each shelf has $\frac{s}{20}$ books.

Note that $20\neq0$. Thus, the division property of equality states that $\frac{f}{20}=\frac{s}{20}$.

In other words, the number of books on each shelf is the same at both places by the division property of equality.

Example 3

Prove the division property of equality using the multiplication property of equality.

Solution

Recall the multiplication property of equality. It states that if $a, b,$ and $c$ are real numbers such that $a=b$, then $ac=bc$.

Using the division property of equality to prove this means first assuming the division property of equality is true. That is, assume $a, b$ are real numbers such that $a=b$ and $c\neq0$. Then $\frac{a}{c}=\frac{b}{c}$.

Note that is $c\neq0$, then $\frac{1}{c}$ is a real number.

Thus, $\frac{a}{\frac{1}{c}}=\frac{b}{\frac{1}{c}}$.

This simplifies to $a\times c=b\times c$ or $ac=bc$.

Thus, if $a, b,$ and $c$ are real numbers such that $a=b$ and $c\neq0$, then $ac=bc$. In other words, the multiplication property of equality holds for any real number $c\neq0$.

But the multiplication property of equality holds for any real number $c$. Therefore, it is required to prove that $a\times0=b\times0$.

Since any number times $0$ is $0$, $a\times0=0$ and $b\times0=0$. Therefore, the transitive property of equality states that $a\times0=b\times0$.

Thus, if the division property of equality is true, the multiplication property of equality is true.

Example 4

Let $x$ be a real number such that $5x=35$. Use the division property of equality to prove that $x=7$.

Solution

It is required to get the variable by itself to solve for $x$. $x$ is multiplied by $5$. This means dividing by $5$ will do just that.

The division property of equality states that doing this to both sides keeps the equality.

Thus, $\frac{5x}{5}=\frac{35}{5}$.

This simplifies to:

$x=7$

Thus, the value of $x$ is $7$.

Example 5

Let $x$ be a real number such that $4x=60$.

Let $y$ be a real number such that $6x=90$.

Prove that $x=y$. Use the division property of equality and the transitive property of equality to do it.

Solution

First, solve for both $x$ and $y$.

$x$ is multiplied by $4$. Thus, isolate the variable by dividing by $4$. However, to keep the equality, the division property of equality requires doing this to both sides.

Thus, $\frac{4x}{4}=\frac{60}{4}$.

This becomesto $x=15$.

$y$ is multiplied by $6$. Thus, isolate the variable by dividing by $6$. However, to keep equality, the division property of equality requires also doing this to both sides.

Thus, $\frac{6x}{6}=\frac{90}{6}$.

This simplifies to $y=6$.

Now $x=6$ and $y=6$. The transitive property of equality states that $x=y$, as required.