- Home
- >
- Equal Vectors – Explanation & Examples
JUMP TO TOPIC
Equal Vectors – Explanation & Examples
 How do you know if two vectors are equal vectors? Is it enough for them to have the same magnitude or same direction? In actuality:
How do you know if two vectors are equal vectors? Is it enough for them to have the same magnitude or same direction? In actuality:
“Two or more vectors are said to be equal if they have the same length or magnitude, and they point in the same direction.”
In this topic, we will discuss the following aspects of equal vectors:
- When are Two Vectors Equal?
- How to Compare the Two Vectors
When are Two Vectors Equal?
Two or more vectors are equal when they have the same length, and they point in the same direction. Any two or more vectors will be equal if they are collinear, codirected, and have the same magnitude.
Mathematically, we can say that two vectors say A and B are equal if they satisfy the following conditions:
A = B (Vector A and B are equal)
If and only if
|A| = |B| (Equal magnitude)
and
A ↑↑ B (Same direction)
If two vectors are equal, their column vectors will also be equal. In other words, two or more vectors are equal if their coordinates are equal.
For example, consider the vectors A = (ax1, ay1) and B = (bx1, by1). If these two vectors are equal, then:
ax1 = bx1 and ay1 = by1.
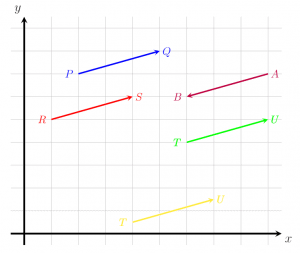
Equal vectors can have different starting and ending points, but their magnitudes and orientation must be the same.
For example, all the vectors except AB in the image below are equal even though they do not overlap. AB is different because, although it has the same magnitude as the others, it does not have the same direction.
How to Compare Two Vectors?
Comparison between vectors is essentially a comparison of the vectors’ magnitudes and directions.
This section will first compare vectors in three different examples to learn more about vector equality. We will then discuss some practice problems and their step-by-step solutions to develop a deeper understanding of this topic.
Examples
Example 1
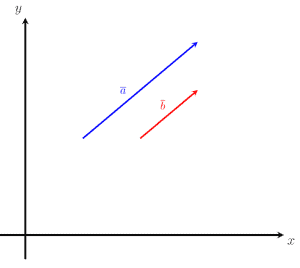
Consider the image given below. Compare the two vectors, a and b, to determine whether they are equal or not.
Solution
By definition, two vectors are equal if and only if they have the same magnitude in the same direction. It can be seen from the figure that vector a and vector b are parallel and pointing in the same direction, but their magnitudes are not equal. Thus, we can conclude that the given vectors are not equal.
a ≠ b
This is equivalent to saying that a vector with the length 5m cannot be equal to a vector whose length is 10m. Two quantities with different magnitudes cannot be equal. The same rule applies to scalars.
Example 2
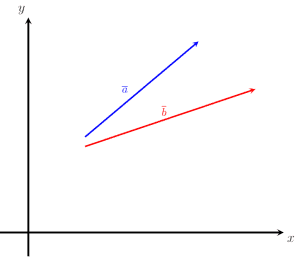
Consider the image given below. Compare the two vectors, a and b, to determine if they are equal or not.
Solution
By definition, two vectors are equal if and only if they have the same magnitude in the same direction. This example is a bit more complicated than the first. It can be seen from the above figure that vectors a and vector b have the same magnitude, but the two vectors are not pointing in the same direction. Thus, again, we can conclude that the given vectors are not equal.
a ≠ b
This is equivalent to a situation where two cars are leaving the same place at the same time. One has a velocity of 50 mph and is traveling northeast. The other car is traveling with a velocity of 50 mph towards the south. After one hour, both of the cars will have traveled 50 miles, but they will have arrived at different destinations. Similarly, the velocity of vectors a and b from the figure cannot be equal. That is, two vectors with the same magnitude and different directions cannot be equal.
Example 3
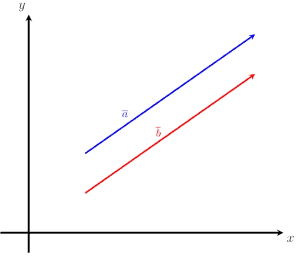
Consider the image given below. Compare the two vectors, a and b, to determine if they are equal or not.
Solution
This example is fairly straightforward. From the above image, it can be seen that vectors a and vector b have the same magnitude. The two vectors are also pointing in the same direction. Therefore, the two vectors are equal to each other.
a = b
These three examples show that two vectors are only equal if they have both the same length and the same direction.
Example 4
Determine the magnitude of two vectors:
- OW, whose initial point is O = (2,5) and final point is W = (5,2), and
- PQ, whose initial point is P = (-4, 2) and final point is Q = (3,6).
Are the two vectors equal or not?
Solution
We can use the distance formula to determine the magnitude of the given vector OW:
|OW| = √ (5-2)^2 + (2-5)^2
Simplifying gives us:
|OW| = √ (3)^2 + (-3)^2
|OW| = √ 9 + 9
|OW| = √ 18
|OW| = √ 2*9
|OW| = √ 2*(3)^2
|OW| = 3 √ 2 units.
Thus, the magnitude of vector OW is approximately 4.242 units.
Now, we determine the magnitude of the given vector PQ:
|PQ| = √ (3-(-4))^2 + (6-2)^2
Simplify to get:
|PQ| = √ (7)^2 + (4)^2
|PQ| = √ 49 + 16
|PQ| = √ 65 units.
Thus, the magnitude of vector PQ is approximately 8.062 units. These two vectors are not equal because neither their magnitudes nor their directions are the same.
OW ≠ PQ
Example 5
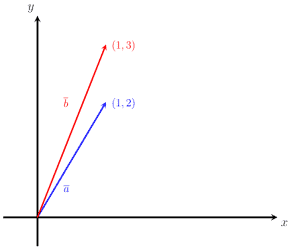
Determine which of the vectors are equal to each other: a = (1; 2), b = (1; 3), and c = (1; 2)
Solution
We will compare the given vectors to determine their magnitudes and directions. We can use this information to decide whether or not they are equal to each other.
First, we determine the magnitudes of the given vectors:
For the vector a = (1; 2):
|a| = √1^2 + 2^2
|a| = √5
For the vector b = (1; 3):
|b| = √1^2 + 3^2
|b| = √1+ 9
|b| = √10
Similarly, for the vector c = (1; 2):
|c| = √1^2 + 2^2
|c| = √5
It is obvious that |a| = |c|, but |a| ≠ |b| and |b| ≠ |c|. Only the magnitudes of the vectors a and c are the same.
To compare the directions, we can plot the three vectors on the coordinate plane, as shown in the image below. It can be observed that all three vectors are parallel to each other with arrows on the same side. That is, they all point in the same direction
a ↑↑ b ↑↑ c same direction
Since vectors a and c have the same length and direction, we can conclude that vectors a and c are equal vectors. The vector b, however, is not equal to a or c
a = c
a ≠ b
b ≠ c
Example 6
Determine the value of x that makes the two vectors A = (2, 10) and B = (2, 5x) equal to each other.
Solution
We know that the given vectors will be equal if their magnitudes and directions are the same. We can find the value of x then as follows:
A = B => (2, 10) = (2, 5x)
Since the two vectors are equal, the x-values and the y-values in the column vectors will be equal. That is:
2 = 2
And
10 = 5x.
By simplifying the above equation, we get:
x = 2
Thus, when x = 2, the two vectors A and B are equal.
Example 7
Determine the value of n that makes the two vectors A = (-5, 1, 3n) and B = (-5, 1, 9) are equal.
Solution
We know that the given vectors will be equal if their magnitudes and directions are the same. We can find the value of x then as follows:
A = B => (-5, 1, 3n) = (-5, 1, 9)
The x, y, and z values of the column vectors must be the same if the vectors are equal to each other. That is:
-5 = -5, 1 = 1, and 3n = 9
By simplifying 3n=9 gives us:
n = 3
Thus, when n = 3 the two vectors A and B are equal.
Example 8
If the two vectors X = (2 – p, 6 – q) and Y = (p – 6, q + 2) are equal determine the following:
- The values of p and q for which the equality holds
- The magnitude of vector X and vector Y
Solution
- Since the two vectors are equal we can write the equation: X = Y => (2 – p, 6 – q) = (p – 6, q + 2)
Setting the x and y values equal to each other gives us:
2-p = p – 6
6-q = q + 2
By simplifying the above equations, we get:
2 – p – p + 6 = 0
2p = 8
p = 4
And
6 – q – q – 2 = 0
2q = 4
q = 2
Thus, when p = 4 and q = 2, the two vectors X and Y will be equal.
2. The magnitude of the vectors X = (-2, 4) and Y = (-2, 4) are:
|X| = √4 + 16
|X| = √20
and
|Y| = √4 + 16
|Y| = √20.
Practice Questions
Determine the magnitude and the direction of the given vectors. Then, check whether they are equal or not.
- A = (-1, -2/3, 0) and V = (2,5,3)
- T = (0, 2, -1) and D = (3,2,5)
- V = (2,5,3) and D = (3,-2,5)
- F = (4,10), G = (5, 5), and H = (4, 10)
- Vector OA where O = (-1,0, 3) and A = (5,2,0); Vector UV, where U = (1, -2, 0) and V = (-2,2, 0).
- Determine the value of n for which the two vectors A = (-2n, 3, 2) and B = (8, 3, 2) will be equal
Answers
- The magnitude of the given vector A is |A| =√ 13/9 units. The magnitude of the given vector V is |V| = √ 38 units. Therefore, the magnitudes are not equal. Their directions are also different, so the given vectors are not equal. A ≠ V
- The magnitude of the vector T is |T| = √ 5 units, and the magnitude of the vector D is |D| = √ 38 units. The given vectors are not equal because both the magnitudes and directions of the vectors are different.
- The magnitude of the given vector V is |V| = √ 38 units, and the magnitude of the vector D is |D| = √ 38 units. Although the two vectors have the same magnitude, their directions are not the same. Therefore the two vectors are not equal.
- The magnitude of F is |F| = √ 116 units. The magnitude of G is |G| = √ 50 units, and the magnitude of H is |H| = √ 116 units. The vectors F and H point in the same direction, but the vector G points in a different direction. Therefore, only vectors F and H are equal. That is, |F| = |H|, |F| ≠ |G|, |G| ≠ |H|, and F ↑↑ .
Thus,
F = H
- The magnitude of the vector OA is |OA|= 7 units, and the magnitude of the vector UV is |UV| = 5 units. Clearly, the two vectors are not equal because their magnitudes are not equal.
- By setting the corresponding x values equal to each other, we find that when n = -4, the two vectors A and B will be equal to each other.
