This problem aims to find the exponential function of a given curve, and there lies a point on that curve at which the solution will proceed. To better understand the problem, you need to have good knowledge of exponential functions and their decay and growth rate techniques.
First, let’s discuss what an exponential function is. An exponential function is a mathematical function denoted by the expression:
\[ f(x) = exp | e^ x \]
This expression refers to a positive value function, or it can also be extended to be complex numbers.
But let’s see how we can understand the concept and figure out if an expression is exponential. If there is an increase of 1 in the exponential value of x, the multiplying factor will always be constant. Also, a similar ratio will be observed when you switch from one term to another.
Expert Answer:
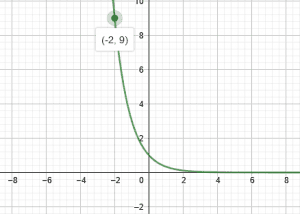
To start with, we are given a point that lies on the curve as shown in the graph figure.
The given point in $x, y$ coordinate system is $(-2, 9)$.
Using our exponential formula:
\[ f(x) = a^ x \]
Here, $a$ refers to the exponent with exponential growth factor $x$.
Now simply plug in the value of $x$ from the given point into our mentioned equation. This will give the value of our unknown parameter $. f$.
\[ 9 = a^ {-2} \]
To equalize the left and right-hand sides, we are going to rewrite $9$ so that the exponents become equal, i.e., $3^ 2$, and this gives us:
\[ 3^2 = a^{-2} \]
Further simplifying:
\[ \left( \dfrac{1}{3} \right) ^{-2}= a^{-2} \]
From the above equation, the variable $a$ can be found as $ \left( \dfrac{1}{3} \right) $
Thus, our exponential function turns out to be:
\[ f = \left( \dfrac{1}{3} \right) ^{x} \]
Numerical Answer
\[ f = \left( \dfrac{1}{3} \right) ^ {x} \]
Example
Determine the exponential function $g(x) = a^x$ whose graph is given.
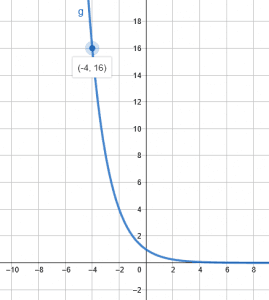
Figure 2
The given point in $x,y$ co-ordinate system is $(-4, 16)$
Step $1$ is using our exponential formula:
\[ g(x) = a ^ x \]
Now plug in the value of $x$ from the given point into our formula equation. This will give the value of our unknown parameter $. g$.
\[ 16 = a ^ {-4} \]
We are going to rewrite $16$ so that the exponents become equal i.e. $2^4$, this gives us:
\[ 2 ^ 4 = a ^ {-4} \]
Simplifying:
\[ \left( \dfrac{1}{2} \right) ^ {-4}= a ^ {-4} \]
The variable $a$ can be found as $ \left( \dfrac{1}{2} \right) $.
Final Answer
\[ g = \left( \dfrac{1}{2} \right) ^ {x} \]
A few things to note here are that the exponential function is important when looking at growth and decay or can be used to determine the growth rate, decay rate, the time passed, and something at the given time.
Images/mathematical drawings are created with GeoGebra.