The question aims to find out the p-value using the given alternative hypothesis, which is a one-sided hypothesis. Therefore, the p-value will be determined for the left tail test with reference to the standard normal probability table.
When the alternative hypothesis states that a certain value for a parameter in the null hypothesis is lesser than the actual value, then left-tail tests are used.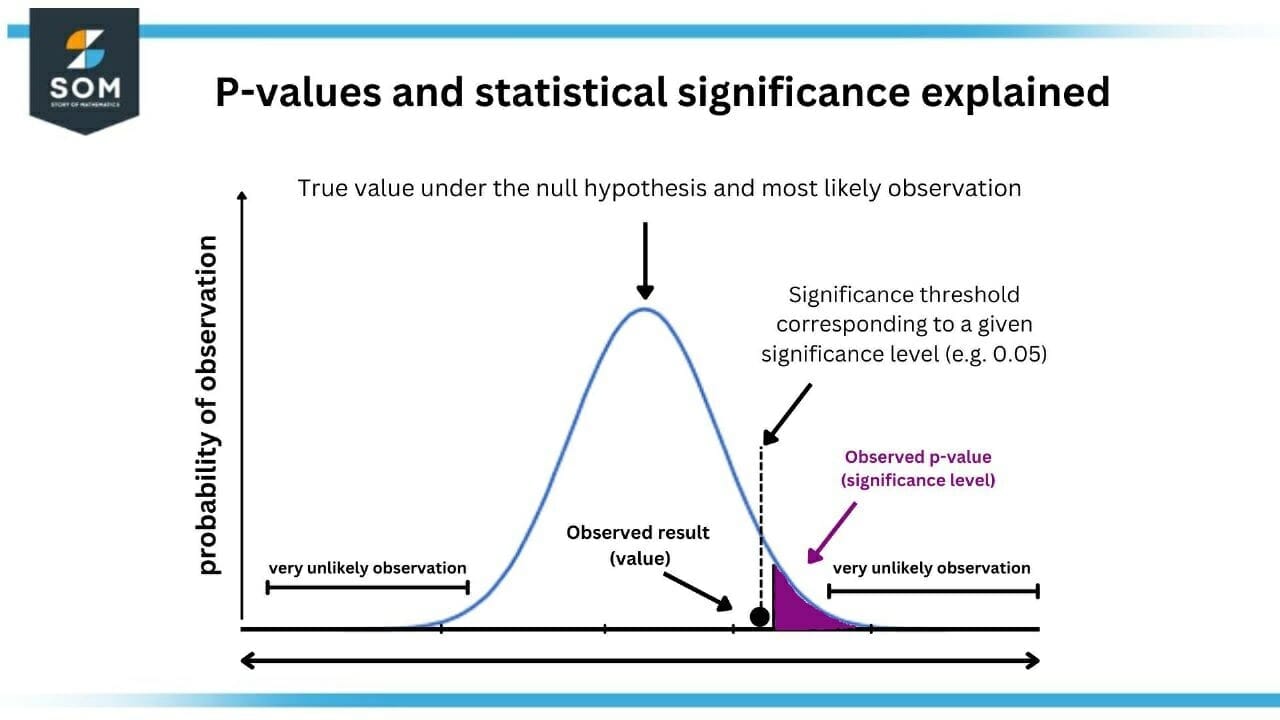
Figure-1 : P-Value and Satistical Significance
Expert Solution:
In order to calculate the p-value, we will use the standard normal table. According to the given information, the value of the test statistic is given as: \[ z = -1.74 \] Null hypothesis $H_o$ is given as: \[ p = 0.5 \] Alternative Hypothesis $H_a$ is given as: \[ p < 0.5 \] The formula for p-value is given as: \[ p = P (Z < z) \] Where P is the probability: \[ p = P (Z < -1.74) \] The p-value can be calculated by determining the probability less than -1.74 using the standard normal table. Therefore, from the table p-value is given as: \[ p = 0.0409 \]Alternative Solution:
For the given problem, the p-value will be determined using the standard probability table. Check against the row starting with -1.74 and column with 0.04. The answer obtained will be: \[ p = P ( Z< -1.74) \] \[ p = 0.0409 \] Therefore, the p-value for $H_a$ < 0.5 is 0.0409.Example:
For a test of $H_o$: \[ p = 0.5 \], the $z$ test statistic equals 1.74. Find the p-value for \[ H_a: p>0.5 \].
Figure-2 : Z-Test Satistic