
This question aims to find the volume of the solid whose base forms an elliptical region. The cross-section perpendicular to the x-axis forms isosceles right triangles with hypotenuse as seen in the line shown in Figure 1.
The concept of this question is based on the basic geometry of shapes like the area and volume of a solid, area of triangles and ellipses and the volume of an arbitrary shape. The given boundary curve forms an ellipse and the equation of the ellipse is given as:
\[ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \]
a is the horizontal distance from the center of the ellipse on either side and b is the vertical distance from the center point on either side. A circle is a special case of an ellipse with a=b=1 with the constant on the right-hand side as the radius of the circle. In this given problem, we will find the volume by the integration of the area of the region.
Expert Answer:
To find the volume of the solid, we need to find the area of the ellipse and then integrate it over the $x-axis$ limits of the given region to get the volume. The boundary curve of the ellipse is given as:
\[ 9x^2 + 4y^2 = 36 \]
We need to convert this boundary curve into the standard ellipse equation, which is given as:
\[ \dfrac{9x^2}{36} + \dfrac{4y^2}{36} = 1 \]
The standard ellipse equation becomes:
\[ \dfrac{x^2}{4} + \dfrac{y^2}{9} = 1 \]
We can find $x$-intercepts of the ellipse by equating $y=0$. This will give us the intersection points of the ellipse on the $x-axis$.
Putting $y=0$, the equation becomes:
\[ \dfrac{x^2}{4} + \dfrac{0}{9} = 1 \]
Simplifying:
\[ x = \pm 2 \]
So the ellipse will intersect the $x-axis$ at $x=-2$ and at $x=2$.
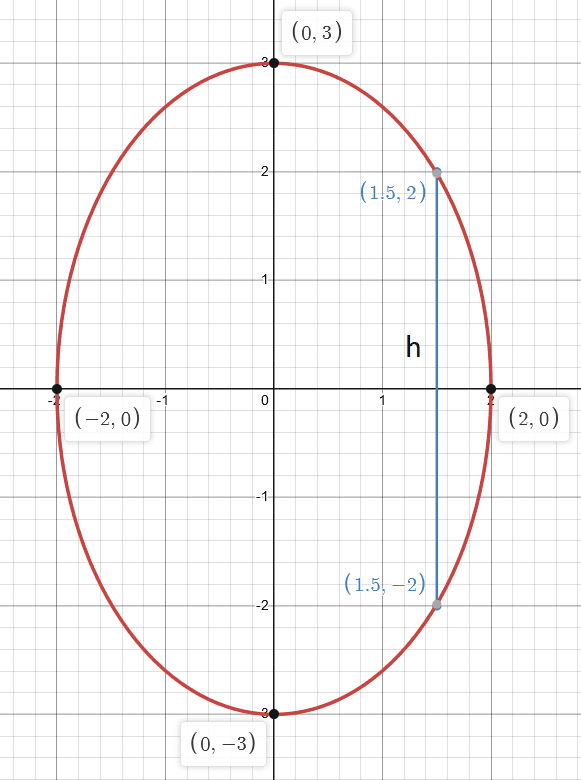
As shown in Figure 1, the cross-section line is the hypotenuse of an isosceles right triangle as given in the question. We can then calculate the side length of the isosceles right triangle. The side length $b$ of right triangle is given by the Pythagoras theorem:
\[ b^2 + b^2 = h^2 \]
Simplifying:
\[ b = \dfrac{h}{\sqrt{2}} \]
We used the same variable $b$ for both sides of the triangle because in an isosceles right triangle, the perpendicular and base have the same length.
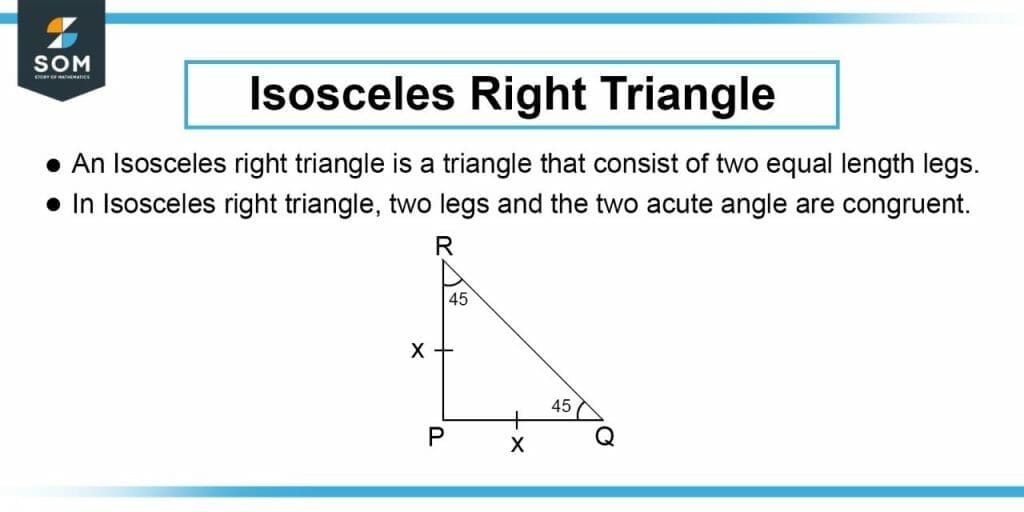
Figure-2 : Isosceles Right Triangle
Area of the triangle is given as:
\[ A = \dfrac{1}{2} b^2 \]
Substituting the value of $b$, we get:
\[ A = \dfrac{h^2}{4} \]
As shown in Figure 1:
\[ h = 2y \]
Substituting this value in the above equation of area, we get:
\[ A = \dfrac{(2y)^2}{4} \]
\[ A = y^2 \]
By rearranging the standard ellipse equation, we can find the value of $y$, which is given as:
\[ y^2 = 9 – \dfrac{9}{4} x^2 \]
Substituting this value above, we get:
\[ A = 9 – \dfrac{9}{4} x^2 \]
Numerical Results:
Integrating the area will give us the volume, which is given as:
\[ V = \int^{2}_{-2} 9 – \dfrac{9}{4} x^2 \, dx \]
Simplifying this equation will give us:
\[ V= 24 \text{units$^{3}$} \]
Example:
The base of $S$ is an ellipse with a boundary curve $3x^2 +9y^2=27$. Given the area of the ellipse, $A=3 – x^2/3$ with cross-sections perpendicular to the $x-axis$ are isosceles right triangles with hypotenuse in the base. Find the volume of the solid.
As the area of the ellipse is given, we can directly find the volume by integrating it over its region. First, we need to find the intersection of the ellipse with $x-axis$. We can calculate that by equating $y=0$, which will become:
\[ x = \pm 3 \]
We can calculate the volume of solid $S$ by integrating the area of the ellipse, which is given as:
\[ V = \int^{3}_{-3} 3 – \dfrac{x^2}{3} \, dx \]
By solving this equation, we get:
\[ V= 12 \text{units$^{3}$} \]
