Forms of Linear Equations- Explanations and Examples

There are three main forms of linear equations. These are the three most common ways of writing the equation of a line so that information about the line is easy to find.

In particular, the three main forms of linear equations are slope-intercept, point-slope, and standard form. Each of these highlights different qualities of the line, but converting one of these forms to another is not difficult.

This article will discuss these three forms of linear equations. Before reading it, however, make sure to review the articles about the slope of a line and the equation of a line.

This topic includes the following subtopics:

What are the Different Forms of Linear Equations?
Point Slope
Slope Intercept
Standard Form

What are the Different Forms of Linear Equations?

Recall that a linear equation is a mathematical equation that defines a line. While each linear equation corresponds to exactly one line, each line corresponds to infinitely many equations. These equations will have a variable whose highest power is 1.

The three main forms of an equation are slope-intercept form, point-slope form, and standard form. These equations give enough information about the line so that we can easily graph them.

What Do We Need to Define a Line?

We need two points to uniquely define a line. If, however, we have a slope and a point, we can easily use the slope to find a second point and graph the line.

Point-slope (or point slope) form and slope-intercept (or slope intercept) form tell us one point and the slope of a line. Standard form gives us two specific points, namely the x- and y-intercepts, though it is not hard to find the slope from the information given.

Point Slope

As the name implies, point-slope form gives one point in a line and its slope. This form is not commonly given to help graph a line. It is, however, more commonly used to get from a verbal description or a graphical depiction of a line to slope-intercept or standard form.

If the given point is (x₁, y₁), a the slope is m, the equation of the line in point-slope form is:

y-y₁=m(x-x₁).

Since there are infinitely many points on every line, there are infinitely many ways to write point-slope form.

Note that one can also use this form if two points are given and neither point is the y-intercept. (Recall that the y-intercept is of the form (0, y₁).) This is because we can use the two points to find the slope. If we have the y-intercept, however, we can skip the point-slope form and use slope-intercept form instead.

Slope Intercept

Slope-intercept form conveys the slope and y-intercept of a line. It is actually technically a special case of point-slope form.

If a line has slope m and y-intercept (0, b), the slope-intercept form is:

y=mx+b.

If this point was written in point-slope form, we would have:

y-b=m(x-0).

Simplifying yields:

y=mx-0+b

y=mx+b.

If the graph of the line is given, we will still have to calculate slope. If the line intersects the y-axis at a clear point, it is best to use that as one of the points used to calculate the slope. Then, we can just plug the values right into the slope intercept equation. If the y-intercept is not clear, however, then the slope-intercept form can be derived from the point-slope equation.

Standard Form

The standard form of an equation is:

Ax+By=C

Where A, B, and C are all whole numbers, and A is not negative.

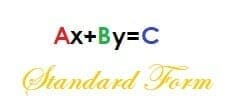
This form is useful in two ways. Namely, it helps us to solve a system of equations and it helps us to find the intercepts of the equation.

Solving Equations

First, the standard form allows us to easily solve systems of equations. Since it only has whole number coefficients, it is simple to line up the variables and then add and subtract the equations.

There are certain strategies, then, that we can employ to find where these equations intersect. In particular, we can multiply the equations so that, for example, the x coefficients are the same. Then, if we subtract the equations, we are left with a one-variable equation with y. Solving for y gives the y-value for the point where the two equations intersect.

Since it doesn’t matter whether we first find the x or y-value of the intersection point, usually people solve for which ever variable makes the calculations easier.

Finding Intercepts

The standard form also makes it easy to find a line’s x- and y-intercepts. Remember that the y-intercept is the y-value when x=0, and the x-intercept is the x-value when y=0. Essentially, they are the points where the line crosses the two axes.

To find the y-intercept, set x=0. Then, we have:

A(0)+By=C

By=C

y=C/B.

Likewise, to find the x-intercept, set y=0. Then, we have:

Ax+B(0)=C

Ax=C

x=C/A.

Examples

This section will cover common examples involving forms of linear equations.

Example 1

What are the slope and y-intercept of a line that passes through the points (1, 2) and (3, 5)?

Example 1 Solution

We know we can find the slope of a line by dividing the difference between the y-values of two points by the difference between the x-values of the same two points. In this case, the slope is:

m=^(2-5)⁄_(1-3)=^-3/_-2=³/_2.

Now, since we have a point and the slope, we can use the point-slope formula. Either point will work, but we can use the smaller values and let (1, 2) be (x₁, y₁).

y-2=³/₂(x-1)

y-2=³/₂x-³/₂

y=³/₂x+¹/₂

Therefore, the slope is ³/₂ and the y-intercept is ¹/₂.

Example 2

What is the slope and intercept of the line shown below?

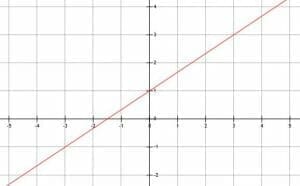
Example 2 Solution

The y-intercept, the point where the line crosses the y-axis, is easy to see. It is (0, 1). We also need to find a second point so that we can find the slope. While there are many options, we can choose (3, 3) for illustration.

The slope is therefore:

m=^(1-3)/_(0-3)=^-2/_-3=²/_3.

Since we already know the intercept, we can just plug the values into the slope-intercept equation to get:

y=²/₃x+1.

Example 3

What is the x-intercept and y-intercept of the line 4x+2y=-7?

Example 3 Solution

Since this equation is already in standard form, we can easily find the intercepts. In this case, A=4, B=2, and C=-7.

Recall that the y-intercept is equal to:

y=^C/_B.

Therefore, the y-intercept is:

y=^-7/₂.

Likewise, recall that the x-intercept is equal to:

x=^C/_A.

Therefore, the x-intercept is:

x=^-7/_4.

Example 4

A line k is y=7/2x-4 in slope-intercept form. Find the standard form of k.

Example 4 Solution

Converting from slope-intercept form to standard form requires some algebraic manipulation.

First, put both the x and y variables on the same side:

y=⁷/₂x-4

^-7/₂x+y=-4

Now, we need to multiply both sides of the equation by the same number so that the coefficients of x and y are both whole numbers. Since the coefficient of x is divided by 2, we should multiply everything by 2:

-7x+2y=-4.

Since A must be positive, we should also multiply the entire equation by -1:

7x-2y=4.

Therefore, A=7, B=-2, and C=4.

Example 5

Write the equation of the line shown below in all three forms. Then, list the slope and both intercepts.

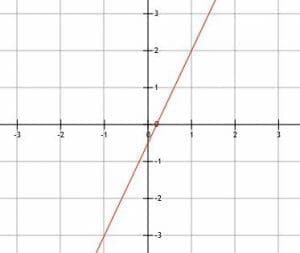
Example 5 Solution

Since we are given the graph, we will have to find two points in order to find the slope. Unfortunately, the y-intercept is not on the grid-lines, so we will have to choose two other points. The points (1, 2) and (-1, -3). Therefore, the slope is:

m=⁽²⁺³⁾/₍₁₊₁₎=⁵/₂=⁵/_2.

Now, we use the point-slope form to find the slope intercept form. Let (1, 2) be the point (x₁, y₁). Then, we have:

y-2=⁵/₂(x-1).

y-2=⁵/₂x-⁵/₂

y=⁵/₂x-¹/_2.

Now, we need to convert this to standard form. As before, we will put the variables on the same side:

^-5/₂x+y=^-1/_2.

Now, we need to algebraically manipulate the equation so that there are no fractions. We can do this by multiplying both sides by 2 to get:

-5x+2y=-1.

Finally, we can multiply both sides of the equation by -1 to ensure that the coefficient of x is positive:

5x-2y=1.

Therefore, the three forms of the equation are:

Point-Slope: y-2=⁵/₂(x-1).

Slope-Intercept: y=⁵/₂x-¹/_2.

Standard: 5x-2y=1.

We can use these equations to derive the intercepts. Slope-intercept form makes it clear that the y-intercept is ^-1/₂. For the x-intercept, we can use the standard form because ^C/_A is the x-intercept. Therefore, the x-intercept is ¹/₅ for this equation.

Slope: ⁵/₂

y-intercept: ^-1/₂

x-intercept: ¹/₅

Practice Problems

Convert the equation 6x-5y=7 into slope-intercept form.
Find the slope-intercept form of the equation for the line that passes through the point (9, 4) and (11, -4).
What is the slope, y-intercept, and x-intercept of the line represented by the equation 2x+5y=1.
Find all three forms of the equation for the line represented below:
Is it possible to write the equation y=^π/₂x+π in standard form as defined here? Why or why not?