Fractional Exponents – Explanation & Examples

Exponents are powers or indices. An exponential expression consists of two parts, namely the base, denoted as b and the exponent, denoted as n. The general form of an exponential expression is b ⁿ. For example, 3 x 3 x 3 x 3 can be written in exponential form as 3⁴ where 3 is the base and 4 is the exponent. They are widely used in algebraic problems, and for this reason, it is important to learn them so as to make studying of algebra easy.

The rules for solving fractional exponents become a daunting challenge to many students. They will waste their valuable time trying to understand fractional exponents but, this is of course a huge mishmash in their minds. Don’t worry. This article has sorted out what you need to do in order to understand and solve problems involving fractional exponents

The first step to understanding how to solve fractional exponents is getting a quick recap what exactly they are, and how to treat the exponents when they are combined either by dividing or multiplication.

What is a Fractional Exponent?

A fractional exponent is a technique for expressing powers and roots together. The general form of a fractional exponent is:

b ^n/m = (^m √b) ⁿ = ^m √ (b ⁿ), let us define some the terms of this expression.

• Radicand

The radicand is the under the radical sign √. In this case our radicand is b ⁿ

• Order/Index of the radical

The index or order of the radical is the number indicating the root being taken. In the expression: b ^n/m = (^m √b) ⁿ = ^m √ (b ⁿ), the order or index of radical is the number m.

• The base

This is the number whose root is being calculated. The base is denoted with a letter b.

• The power

The power determines how many times the value is root is multiplied by itself to get the base. It is normally denoted with a letter n.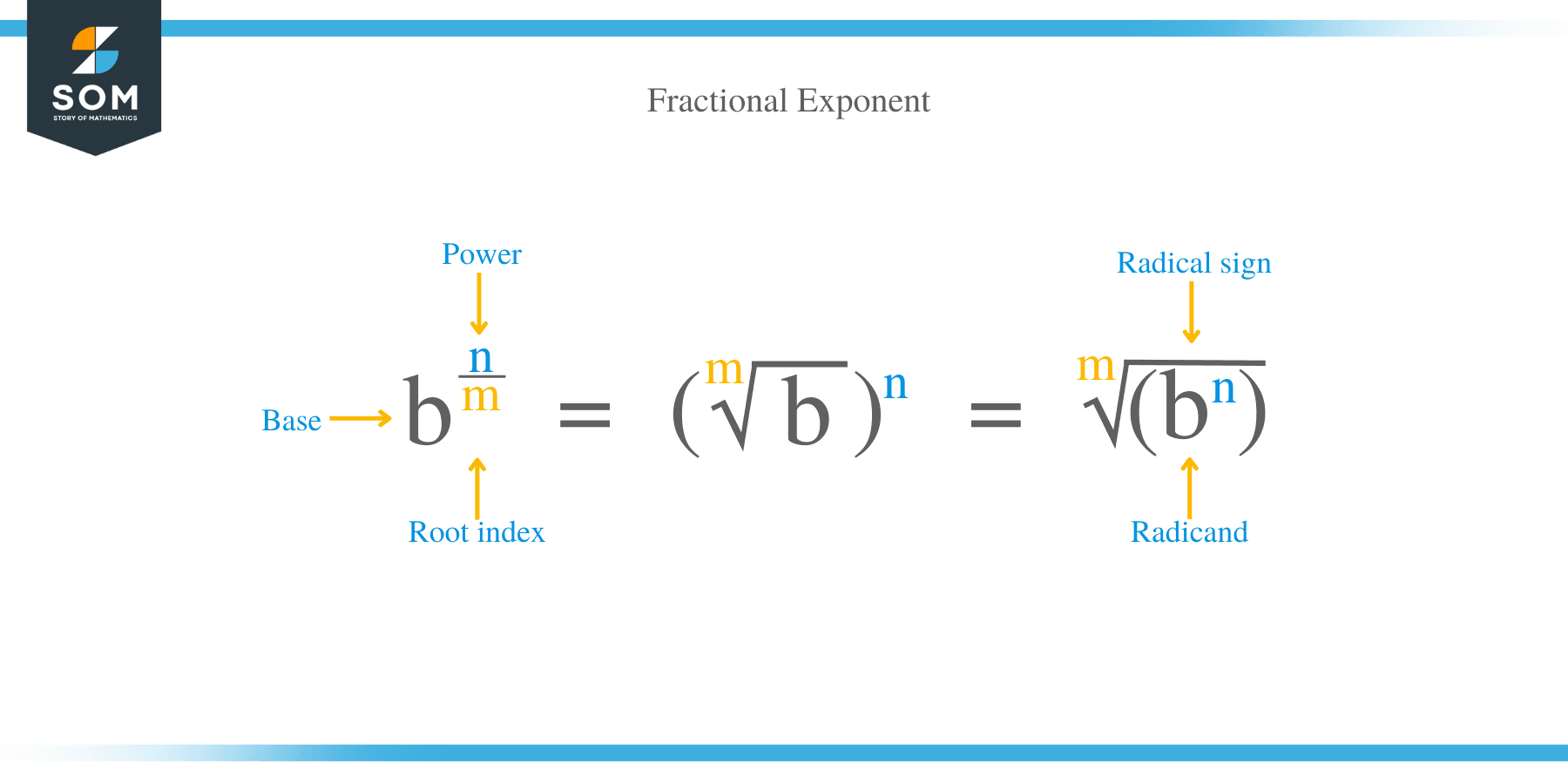

How to Solve Fractional Exponents?

Let’s know how to solve fractional exponents with the help of examples below.

Examples

• Calculate: 9 ^½ = √9

= (3²)^1/2

= 3

• Solve: 2^3/2= √ (2³)

= 2.828

• Find: 4^3/2

4^3/2 = 4 ^{3× (1/2)}

= √ (4³) = √ (4×4×4)

= √ (64) = 8

Alternatively;

4^3/2 = 4 ^{(1/2) × 3}

= (√4)³ = (2)³ =

• Find the value of 27^4/3.

27^4/3 = 27^{4 × (1/3)}

= ∛ (27⁴) = ³√ (531441) = 81

Alternatively;

27^4/3 = 27^{(1/3) × 4}

= ∛ (27)⁴ = (3)⁴ = 81

• Simplify: 125^1/3
  125^1/3 = ∛125
  = [(5) ³]^1/3
  = (5)¹
  = 5
• Calculate: (8/27)^4/3
  (8/27)^4/3
  8 = 2³and 27 = 3³
  So, (8/27)^4/3 = (2³/3³)^4/3
  = [(2/3) ³]^4/3
  = (2/3) ⁴
  = 2/3 × 2/3 × 2/3 × 2/3
  = 16/81

How to multiply Fractional Exponents with the Same Base

Multiplying terms having the same base and with fractional exponents is equal to adding together the exponents. For example:

x^1/3 × x^1/3 × x^1/3 = x ^{(1/3 + 1/3 + 1/3)}

= x¹ = x

Since x^1/3 implies “the cube root of x,” it shows that if x is multiplied 3 times, the product is x.

Consider another case where;

x^1/3 × x^1/3 = x ^{(1/3 + 1/3)}

= x^2/3, this can be expressed as ∛x ²

Example 2

Workout: 8^1/3 x 8^1/3

Solution

8^1/3 x 8^1/3 = 8 ^{1/3 + 1/3} = 8^2/3

= ∛8²

And since the cube root of 8 can be found easily,

Therefore, ∛8² = 2² = 4

You may also come across multiplication of fractional exponents having different numbers in their denominators, in this case, the exponents are added the same way fractions are added.

Example 3

x^1/4 × x^1/2 = x ^{(1/4 + 1/2)}

= x ^{(1/4 + 2/4)}

= x^3/4

How to divide Fractional Exponents

When dividing fractional exponent with the same base, we subtract the exponents. For instance:

x^1/2 ÷ x^1/2 = x ^{(1/2 – 1/2)}

= x⁰ = 1

This implies that, any number divided by itself is equivalent to one, and this makes sense with the zero-exponent rule that, any number raised to an exponent of 0 is equals one.

Example 4

16^1/2 ÷ 16^1/4 = 16^{(1/2 – 1/4)}

= 16^{(2/4 – 1/4)}

= 16^1/4

= 2

You can notice that, 16^1/2 = 4 and 16^1/4 = 2.

Negative fractional exponents

If n/m is a positive fractional number and x > 0;
Then x^-n/m = 1/x ^n/m = (1/x) ^n/m, and this implies that, x^-n/m is the reciprocal of x ^n/m.

In general; if the base x = a/b,

Then, (a/b)^-n/m = (b/a) ^n/m.

Example 5

Calculate: 9^-1/2

Solution
9^-1/2
= 1/9^1/2
= (1/9)^1/2
= [(1/3)²]^1/2
= (1/3)¹
= 1/3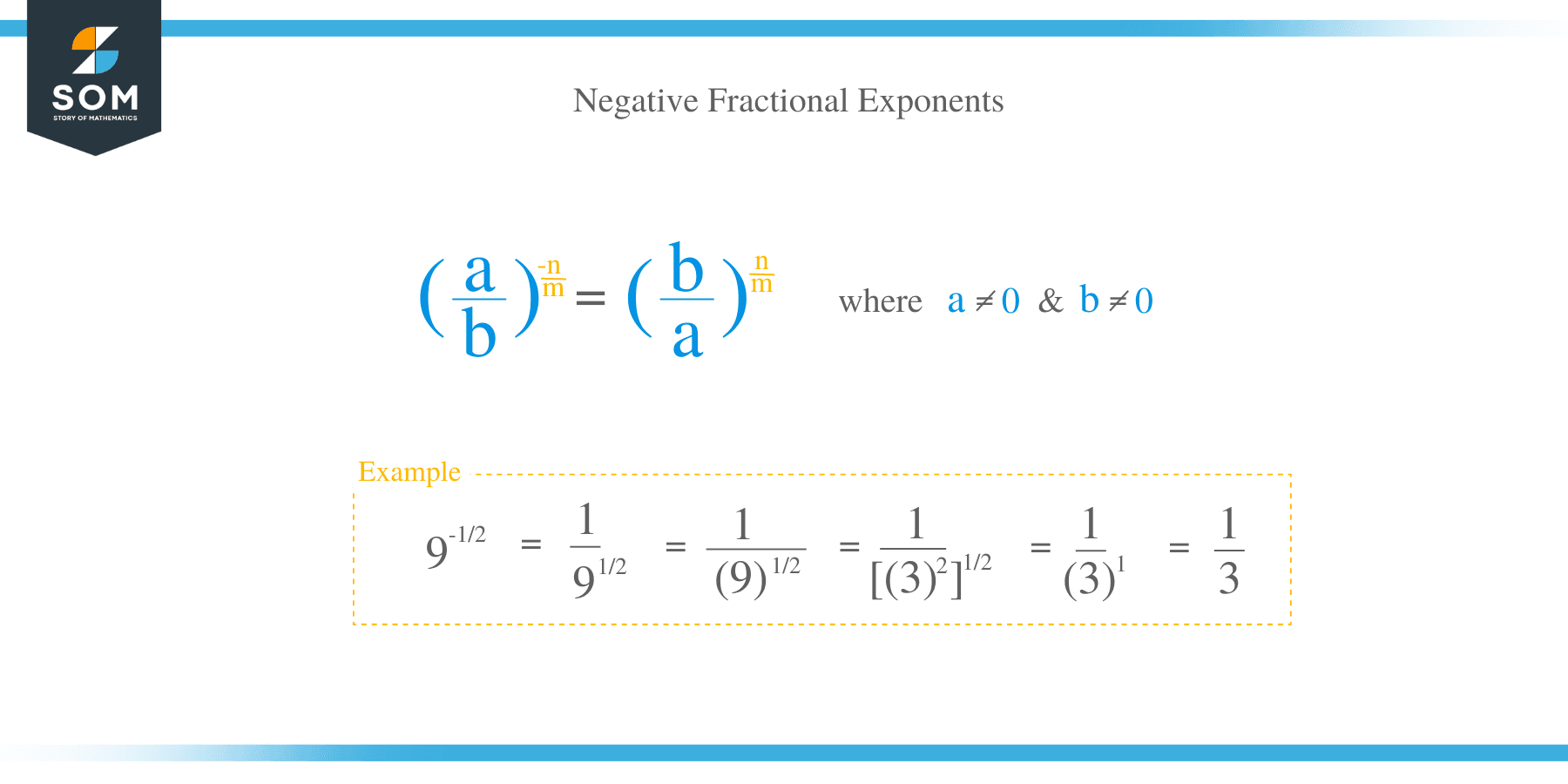

Example 6

Solve: (27/125)^-4/3

Solution
(27/125)^-4/3
= (125/27)^4/3
= (5³/3³)^4/3
= [(5/3) ³]^4/3
= (5/3)⁴
= (5 × 5 × 5 × 5)/ (3 × 3 × 3 × 3)
= 625/81