- Home
- >
- Geometric Construction – Explanation & Examples
Geometric Construction – Explanation & Examples
 Geometric construction is the process of creating geometric objects using only a compass and a straightedge.
Geometric construction is the process of creating geometric objects using only a compass and a straightedge.
While it may seem surprising, we can create almost any geometric object — including lines, circles, squares, triangles, angles, and more — using only these two tools!
Geometric construction is part of pure geometry (also known as synthetic geometry or axiomatic geometry). This is the geometry that does not rely on equations and coordinate systems. Instead, it relies on constructions and proofs based on predetermined axioms.
In this article, we will discuss the following subtopics of geometric construction:
- What is Geometric Construction?
- How to Do Constructions in Geometry?
- Types of Construction in Geometry.
What is Geometric Construction?
Geometric construction is the process of creating geometric objects using only a compass and a straightedge. It is a component of pure geometry, which, unlike coordinate geometry, does not use numbers, formulae, or a coordinate system to create and compare geometric objects.
A compass is a device with a handle and two legs. One leg has a point at the end, and the other has a pencil or graphite piece. The two legs are hinged so that the user can change how far apart they are. Compasses have been used since antiquity to draw circles and arcs.
A straightedge is any physical object with a solid, (you guessed it) straight edge that can be traced with a pencil. Note that while many people use a ruler as a straightedge in geometric constructions, technically, a straightedge should not include numbers. Using a ruler is okay as long as you ignore the temptation to compare lines using its measurements.

Geometric constructions (and their accompanying proofs) rely on a certain set of agreed-upon rules called axioms. These essentially give us the tools we need to make a proof and ensure that all readers are working with the same definitions.
Euclid
Euclid of Alexandria is sometimes called the founder of geometry because his work in pure geometry was well-formulated and well-distributed. In fact, his primary work, Euclid’s Elements, is one of the most widely circulated books of all time. Until the 20th century, every educated person would have taken a course on Euclid’s Elements.

Euclid included 23 definitions, five postulates, and five common notions. The definitions ensured that Euclid and any readers were on the same page regarding what words meant. The common notions provided the logical steps necessary for proving that the constructions worked, while the postulates were essentially foundational “facts” that did not need to be proved.
While many of the propositions in Euclid’s Elements were just proofs that constructions were possible, others were proofs about comparing geometric objects or proofs that established facts about them. However, in these latter proofs, Euclid often still included a simple construction as an illustration or reference for the proof.
Other Geometries
While Euclid’s geometric constructions and proofs have stood the test of time, they are not the only set of axioms, nor are his constructions the only ones. Other geometers, including Riemann and Gauss, developed their own axiom systems that led to different geometries. These are generally known as “non-Euclidian” geometries, and many involve removing or negating Euclid’s fifth postulate, which states that:
“If a line segment intersects two straight lines forming two interior angles on the same side that sum to less than two right angles, the the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.”
A simple way to conceive of non-Euclidean geometry is to consider what happens when our drawing surface is the surface of a sphere instead of a flat plane. On such a surface, it is possible to draw a triangle with straight lines but two right angles.
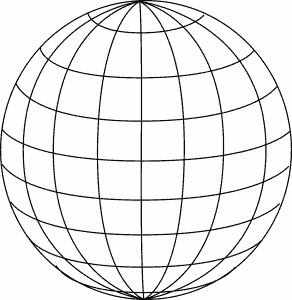
How to do Constructions in Geometry?
Constructions in geometry are based on circles and lines. This is because of the two basic shapes we can make with a straightedge and a compass.
Making a line with a straightedge is pretty simple. Just put the edge of straightedge wherever you want the line. Then, use a pencil to draw the line, keeping the pencil close to the edge of the straightedge and holding the straightedge steady with your non-dominant hand. You can use the pencil from the compass, but it is sometimes handy to have another one ready to go.
To make a circle with a compass, put the point wherever you want the center to be. Then, put the pencil tip at any point on the desired circumference. Next, rotate the pencil in a circle, holding the point steady. If your compass has a lock function, now is the time to use it so that the distance between the legs doesn’t change. When you get back to the starting point, you will have a perfect circle.
Types of constructions geometry
While there are many things you can make with just a ruler and a compass, we’ll divide them into broad categories here to give you an idea of the possibilities. Remember that each construction starts with a “given.” These are the things already on your plane. For example, a construction that requires you to draw a circle with a center at a certain point and a distance the length of a certain line will already have the point and the line drawn on the plane.
Bisections
Using just a compass and a ruler, we can cut a line or angle in half. We can also use similar processes to cut a circle, triangle, or other polygons into two equal parts. Using the same principles, we can cut the same objects into fourths, eighths, sixteenths, etc.
Copies
If you are given a line, angle, circle, triangle, etc., you can make a copy of it using your straightedge and compass in another place. These constructions will often ask you to put the copy in a specific place, such as a given point or on a given line.
Angles
Remember that there are no specific measurements in constructions. That being said, you can copy an angle regardless of the measurement without a protractor by just using a straightedge and compass. You can also create angles of many different measures (for example, 60 degrees, 30 degrees, 75 degrees, etc.) using construction methods.
Triangles
In addition to copying triangles, you can use construction methods to make triangles with any three given side lengths. You can also make equilateral triangles. Construction methods are also useful for proving facts about triangles, such as the fact that the angles as the base of isosceles triangles are equal. You can even use them to prove that two or more triangles are congruent.
Other Shapes
Finally, you can even use construction methods to make squares, regular pentagons, and regular hexagons.
Examples
Examples in construction are a little different from examples in other sections. Nonetheless, there are still a few examples that will help illustrate how construction works.
Example 1
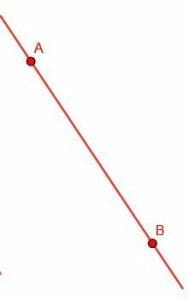
Connect two points with a line.

Example 1 Solution
First, draw a line between these two points, line up your straightedge so that the edge touches both points. Then, use a pencil and trace along the edge of your straight edge. It’s okay if the line segment you draw extends beyond the points.
That’s all there is to it! You will end up with a picture like the one below.
Example 2
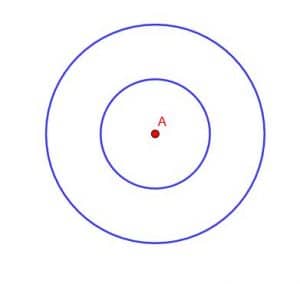
Create two different circles with center at A.

Example 2 Solution
There are infinitely many solutions to this problem, but all can be found in the same way.
First, put the point of your compass at A. Then, set your compass to a small distance, put the pencil or graphite to the paper, and draw a circle.
Now, set your compass to the largest distance possible. Put the point at A, set the pencil or graphite to the paper, and draw another circle.
The result will be two circles, centered at A. One of the circles will be inside the other, as shown.
Example 3
Connect the three points to form a triangle.
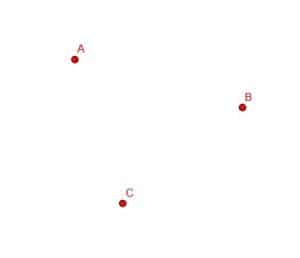
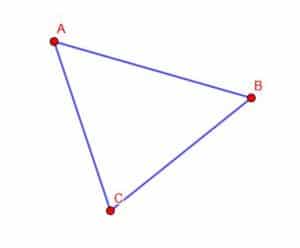
Example 3 Solution
This problem is similar to the one in example 1. Instead of just connecting two points, we need to connect three for a total of three lines.
First, line the straightedge up so that the edge touches points A and B. Then, trace along the edge to connect the two.
Next, do the same thing for the points A and C and then the C and B points. The resulting figure should look like the one below.
Example 4
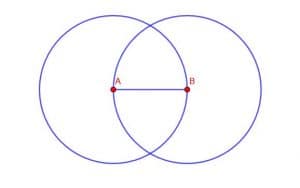
Connect the points A and B. Then, make a circle with center A and radius AB. Then, make a circle with center B and radius BA.

Example 4 Solution
Our first step is to connect points A and B as before. First, line up the straightedge so that the edge touches A and B. Then, trace along the edge to create the line.
Now, to make the first circle, put the point of the compass at A and the pencil at B. Then, holding your hand steady, pivot the compass around the point to create a circle.
Next, place the point on B and the pencil tip on A. As before, hold your hand steady while pivoting the compass around the point and drawing out the circumference of the circle.
Your final figure will look like the one below.
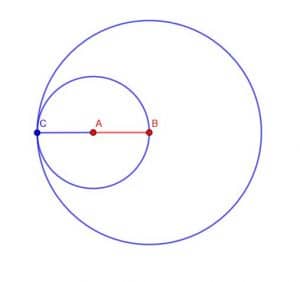
Example 5
Given the line AB, create a circle with center A and radius AB. Then, create a circle with center B and radius equal to the diameter of the first circle.

Example 5 Solution
The first step is similar to what we have done before. We will place the point of the compass at A and the pencil tip at B. Then, holding our hand steady, we can trace out the circle’s circumference by pivoting the compass around the point until we get back to B.
Next, we want a circle with center B and radius equal to the other circle’s diameter. How do we know which point on the circle is the furthest from B?
We can actually use Euclid’s second postulate, which says that we can use construction methods to extend any line segment. Thus, we line our straightedge up so that the edge touches A and B. We also want to make sure that the straightedge extends far enough to intersect with the circumference of the circle on the other side of B. We can trace along the edge and label the intersection of this line and the circle as C. BC is the circle’s diameter.
Now, we can put the point of the compass at B and the pencil at C. Holding it steady, we then pivot the compass around the point and trace out the circumference of the larger circle until we get back to C. The final figure will look similar to the one below.
Practice Questions
![]()
Open Problems
- Construct two circles that touch at exactly one point, such that one is not inside the other.
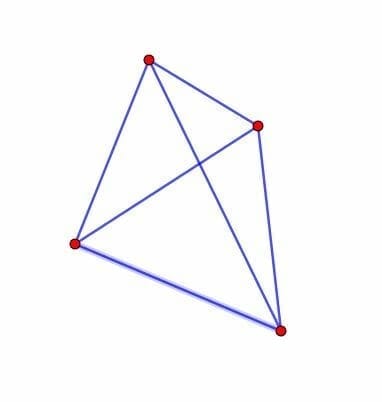
- Draw lines connecting all four points so that each point connects.

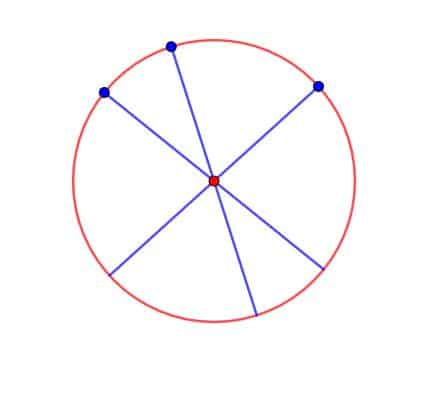
- Draw three diameters through the circle.

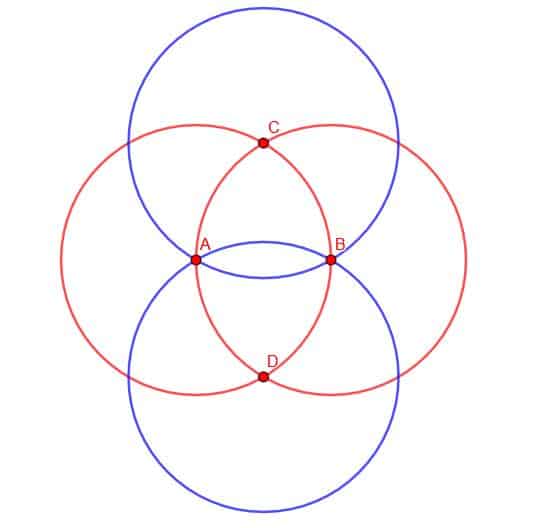
- Draw two more circles, one with radius CA and the other with radius DA.

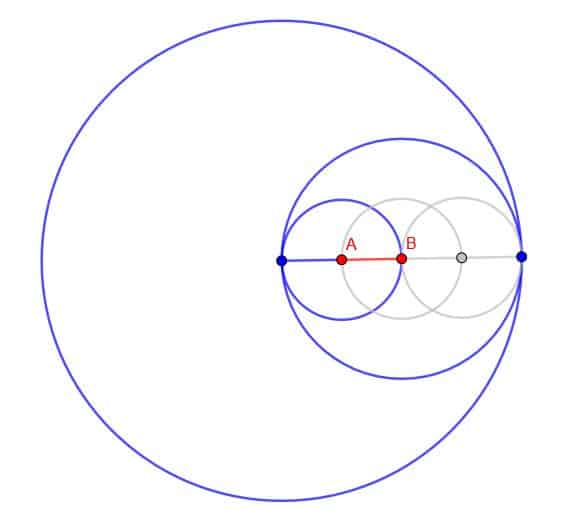
- Draw a circle with radius four times the length of AB.