Graphing Reciprocal Functions – Explanation and Examples
Reciprocal functions have the form y=k/x, where k is any real number. Their graphs have a line of symmetry as well as a horizontal and vertical asymptote.
The key to graphing reciprocal functions is to familiarize yourself with the parent function, y=k/x. Other reciprocal functions are generally some sort of reflection, translation, compression, or dilation of this function. Consequently, it is important to review the general rules of graphing as well as the rules for graph transformations before moving on with this topic.
In this section, we will discuss:
- What is a Reciprocal Function on a Graph?
- How to Graph Reciprocal Functions
What is a Reciprocal Function on a Graph?
A reciprocal function has the form y=k/x, where k is some real number other than zero. It can be positive, negative, or even a fraction.
The graph of this function has two parts. For the simplest example of 1/x, one part is in the first quadrant while the other part is in the third quadrant.
In the first quadrant, the function goes to positive infinity as x goes to zero and to zero as x goes to infinity. In the third quadrant, the function goes to negative infinity as x goes to zero and to zero as x goes to negative infinity.
Why are They Called Reciprocal Functions?
When we think of functions, we usually think of linear functions. These have the form y=mx+b.
Recall that a reciprocal is 1 over a number. For example, the reciprocal of 2 is 1/2. Reciprocal functions are the reciprocal of some linear function.
For example, the basic reciprocal function y=1/x is the reciprocal of y=x. Likewise, the reciprocal of y=(2/3)x+4 is y=(3/2x+12).
In fact, for any function where m=p/q, the reciprocal of y=mx+b is y=q/(px+qb).
How to Graph Reciprocal Functions
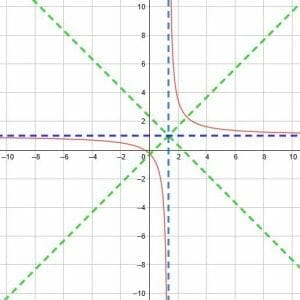
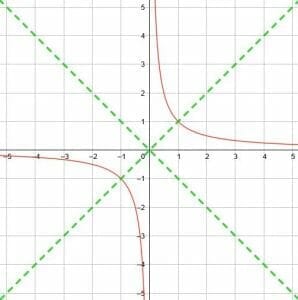
The basic reciprocal function y=1/x. It has a vertical asymptote at x=0 and a horizontal asymptote at y=0. It also has two lines of symmetry at y=x and y=-x.
Other reciprocal functions are translations, reflections, dilations, or compressions of this basic function. They will also, consequently, have one vertical asymptote, one horizontal asymptote, and one line of symmetry. These three things can help us to graph any reciprocal function.
Horizontal Asymptote
A horizontal asymptote is a horizontal line that a function approaches as x gets closer and closer to a specific value (or positive or negative infinity), but that the function never reaches.
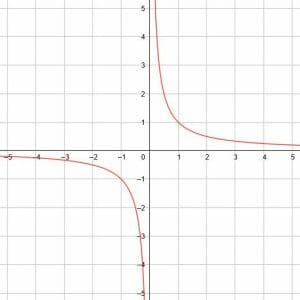
In the basic function, y=1/x, the horizontal asymptote is y=0 because the limit as x goes to infinity and negative infinity is 0.
Any vertical shift for the basic function will shift the horizontal asymptote accordingly.
For example, the horizontal asymptote of y=1/x+8 is y=8. The horizontal asymptote of y=1/x-6 is y=-6.
Vertical Asymptote
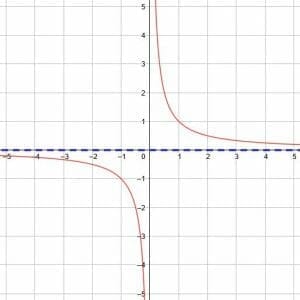
The vertical asymptote is similar to the horizontal asymptote. It is the point of discontinuity in the function because, if x=0 in the function y=1/x, we are dividing by zero. Since this is impossible, there is no output for x=0.
But, what about when x=0.0001? Or when x=-0.0001?
Our x-values can get infinitely close to zero, and, as they do, the corresponding y-values will get infinitely close to positive or negative infinity, depending which side we approach from. As x goes to zero from the left, the values go to negative infinity. When x goes to zero from the right, the values go to positive infinity.
Every reciprocal function has a vertical asymptote, and we can find it by finding the x value for which the denominator in the function is equal to 0.
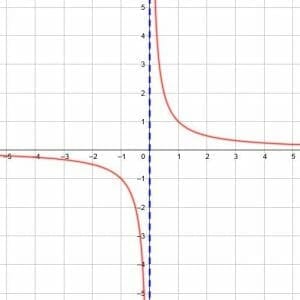
For example, the function y=1/(x+2) has a denominator of 0 when x=-2. Therefore, the vertical asymptote is x=-2. Likewise, the function y=1/(3x-5) has a denominator of 0 when x=5/3.
Note that the location of the vertical asymptote is affected both by translations to the left or right and also by dilation or compression.
Lines of Symmetry
To find the lines of symmetry, we have to find the point where the two asymptotes meet.
If our reciprocal function has a vertical asymptote x=a and a horizontal asymptote y=b, then the two asymptote intersect at the point (a, b).
Then, the two lines of symmetry are y=x-a+b and y=-x+a+b.
This makes sense because we are essentially translating the functions y=x and y=-x so that they intersect at (a, b) instead of (0, 0). Their slopes are always 1 and -1.
Consequently, the two lines of symmetry for the basic reciprocal function are y=x and y=-x.
Examples
In this section, we will go over common examples of problems involving graphing reciprocal functions and their step-by-step solutions.
Example 1
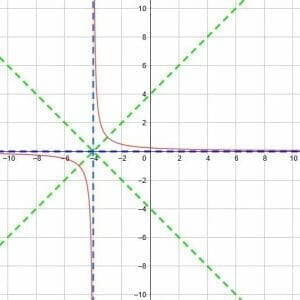
Find the vertical asymptote, the horizontal asymptote, and the lines of symmetry for the reciprocal function y=1/(x+4).
Then, graph the function.
Example 1 Solution
We’ll start by comparing the given function to the parent function, y=1/x.
The only difference between the two is that the given function has x+4 in the denominator instead of x. This means that we have a horizontal shift 4 units to the left from the parent function.
Thus, our horizontal asymptote, y=0, will not change. Our horizontal asymptote, however, will move 4 units to the left to x=-4.
Therefore, the two asymptotes meet at (-4, 0). This means that the two lines of symmetry are y=x+4+0 and y=-x-4+0. Simplifying, we have y=x+4 and -x-4.
Thus, we can graph the function as below, where the asymptotes are given in blue and the lines of symmetry given in green.
Example 2
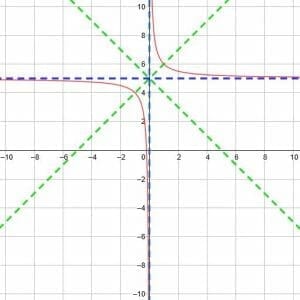
Find the vertical asymptote, the horizontal asymptote, and the lines of symmetry for the reciprocal function y=1/x+5. Then, graph the function.
Example 2 Solution
As before, we can compare the given function to the parent function y=1/x. In this case, the only difference is that there is a +5 at the end of the function, signifying a vertical shift upwards by five units.
Otherwise, the function should be essentially the same. This means that the vertical asymptote is still x=0, but the horizontal asymptote will also shift upwards five units to y=5.
The two asymptotes will meet at the point (0, 5). From this, we know that the two lines of symmetry are y=x-0+5 and y=x+0+5. That is, the two lines are y=x+5 and y=-x+5.
From this information, we can graph the function as shown below.
Example 3
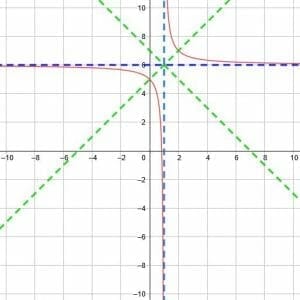
Find the vertical asymptote, the horizontal asymptote, and the lines of symmetry for the reciprocal function y=1/(x-1)+6.
Then, graph the function.
Example 3 Solution
Once more, we can compare this function to the parent function. This time, however, this is both a horizontal and a vertical shift. Since the denominator is x-1, there is a horizontal shift of 1 unit to the right. The +6 at the end signifies a vertical shift of six units upwards.
Therefore, the vertical asymptote is shifted to the left one unit to x=-1. The horizontal asymptote is likewise shifted upwards six units to y=6, and the two will meet at (-1, 6).
Using this intersection, the lines of symmetry will be y=x-1+6 and y=-x+1+6. These simplify to y=x+5 and y=-x+7.
Thus, we can graph the function as shown below.
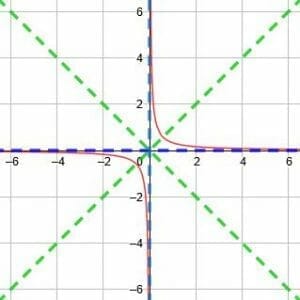
Example 4
Find the vertical asymptote, the horizontal asymptote, and the lines of symmetry for the reciprocal function y=1/3x.
Then, graph the function.
Example 4 Solution
In this case, there is no vertical or horizontal shift. This means that the asymptotes will remain at x=0 and y=0. Likewise, the lines of symmetry will still be y=x and y=-x.
So what has changed?
The shape of the two parts of the functions has changed slightly. Multiplying x by a number greater than one causes the curves to become steeper. For example, the curve in the first quadrant will become more like an L.
Conversely, multiplying x by a number less than 1 but greater than 0 will make the slope of the curve more gradual.
The points that intersect the line of symmetry with a positive slope will also be closer together when x is multiplied by larger numbers and further apart when x is multiplied by smaller numbers.
In the end, we have the function shown below.
Example 5
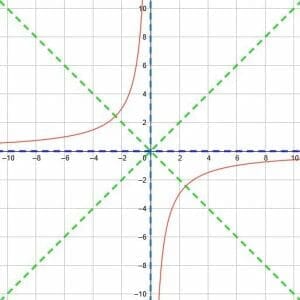
Find the vertical asymptote, the horizontal asymptote, and the lines of symmetry for the reciprocal function y=-6/x.
Then, graph the function.
Example 5 Solution
Similar to Example 4, we have no horizontal or vertical shift in this function. That means that our vertical asymptote is still x=0, the horizontal asymptote is y=0, and the two lines of symmetry are y=x and y=-x.
So again, we need to ask, what has changed?
First, we need to notice that 6/x=1/(1/6)x. Then, we can see that this situation is exactly the opposite of example 4. Now, we are multiplying x by a number less than 1, so the curve of the two parts of the function will be more gradual, and the points where they intersect the line of symmetry will be further apart.
Notice, however, that this function has a negative sign as well. Consequently, we need to reflect the function over the y-axis. Now, the two parts of the function will be in quadrants 2 and 4.
Therefore, we end up with the function shown below.
Example 6
Find the vertical asymptote, the horizontal asymptote, and the lines of symmetry for the reciprocal function y=5/(3x-4)+1.
Then, graph the function.
Example 6 Solution
There is a lot of things happening in this function. First, let’s find the vertical and horizontal shifts so we can find the asymptotes and the line of symmetry.
This function has a denominator of 0 when x=4/3, which is consequently the vertical asymptote. Unlike previous examples, the horizontal compression does have an effect on the vertical asymptote.
The function also has a +1 at the end, which means it has a vertical shift one unit upward. This means that the horizontal asymptote is y=1.
Now, we know that the two asymptotes will intersect at (4/3, 1). This means that the lines of symmetry are y=x-4/3+1 and y=x+4/3+1. These simplify to y=x-1/3 and y=x+7/3.
Now we need to account for the dilation of the function before we can graph it. Technically, we can rewrite this function as y=5/(3(x-4/3)) or even as y=1/((3/5)(x-4/3)). Even though this seems more complicated, it makes it easier to see that the factor in front of x is 3/5, which is less than 1. Therefore, the curves are less steep, and the points where they intersect the line of symmetry are further apart.
Finally, we end up with a function like the one shown below.
