- Home
- >
- Greater than – Explanation & Examples
JUMP TO TOPIC
Greater than – Explanation & Examples
 What is Greater Than Sign?
What is Greater Than Sign?
The greater than sign is a mathematical symbol used to denote an inequality between two variables or quantities. This sign has been in use since the 1560s. The sign normally resembles equal – length strokes connecting in acute angle (>).
The symbol is usually placed between two quantities being compared, and it normally shows that the first variable is bigger than the second variable. The greater than sign has been used in computer programming languages to perform other operations
For example, 2 > 1 and 1 > −2. This indicates that 2 is greater than 1 and 1 is greater than negative two.
Some of the examples greater than sign are:
5 > 2: This inequality shows that 5 is greater than 2
45 > 30: 45 is greater than 30
10/2 > 6/3: We can simplify this inequality as 5 > 2: which implies that 5 is greater than 2
0.01 > 0.001 implies that 0.01 is greater than 0.001
2 > -2: In this case, it obvious that positive numbers are greater than negative numbers. Therefore 2 is greater than – 2.
How to Remember Greater than Sign?
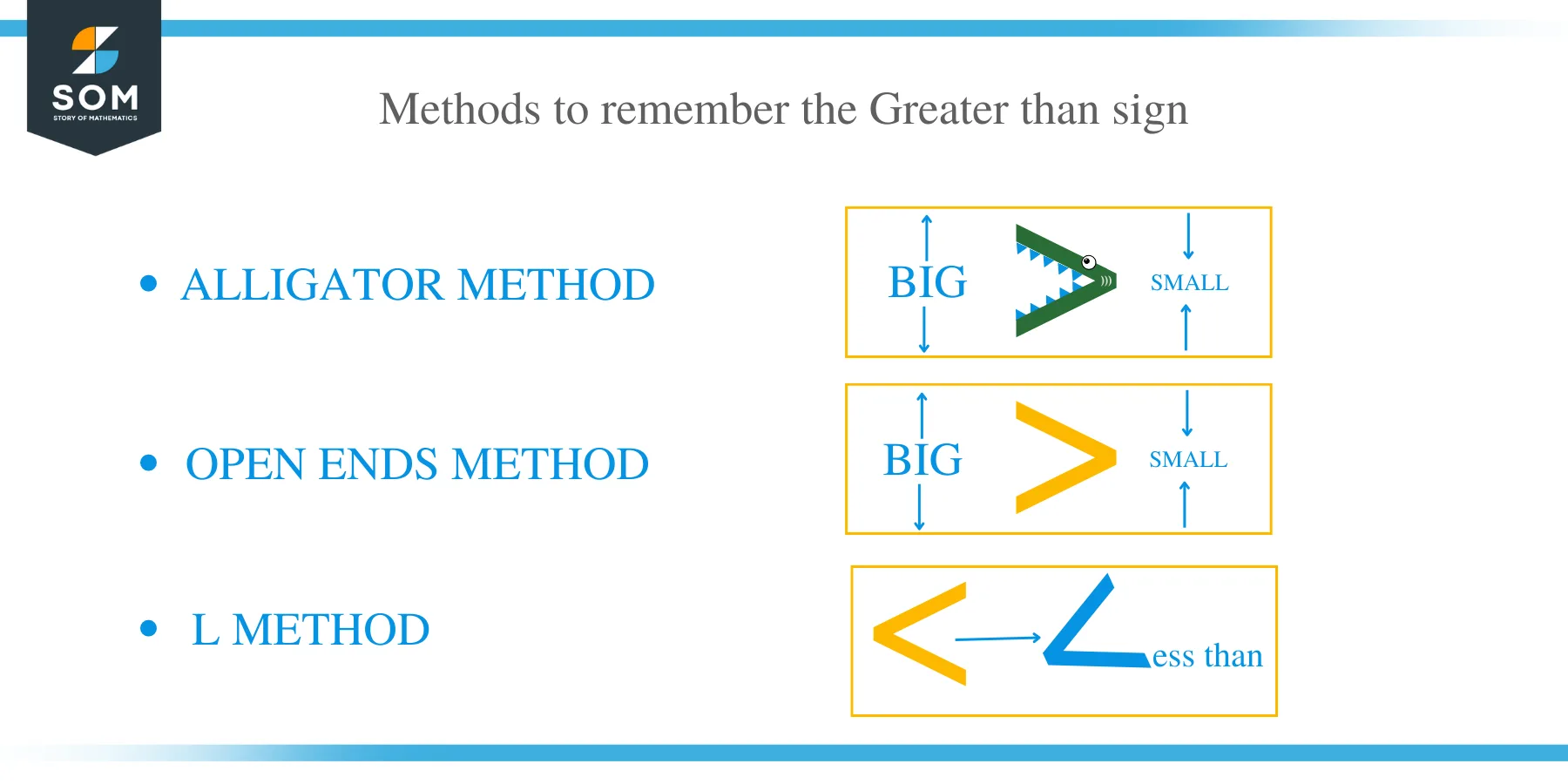
There are 3 methods to remember the Greater than sign.
The alligator method of remembering greater than symbol
The alligator method is the simplest technique for remembering the greater than symbol. Always remind yourself of the alligator when comparing variables using the greater than symbol. The alligator’s mouth is always wide open to swallow or gulp as much food as possible. The mouth of the alligator usually opens to the left.
The open ends method of remembering greater than symbol
Another easy way to recall the greater than is to remember that open ends of the sign normally face the bigger number, and the arrow points to the smaller number.
L Method
In this method, recall that the less than starts with the letter L resembles the less than symbol, whereas the greater than symbol does not resemble and sign, therefore because the greater than sign does not look like an L, it cannot there be “less than.”
 Solving Greater than Problems
Solving Greater than Problems
Before attempting to solve any problem pertaining greater than symbol, the following considerations are made:
- Go through the entire question to understand it.
- Highlight the keywords to help in solving the problem
- Identify the variables
- Write the mathematical expression of the problem using the inequality symbol.
- Justify the expression
Example 1
Saleh has $500 in his savings account at the end of the year. He intends to use at least 200 USD in the account by the start of the following year. If he makes a weekly withdrawal of $25, write an expression describing this situation.
Solution
Start by identifying important keywords.
Assume the variables and let w represent the number of weeks
Therefore, the representation of this situation is:
500 – 25w ≥ 200
In this situation, the greater than or equal sign has been used to cater to the amount to be spent should amount to 200 USD.
Example 2
Brian has fifteen oranges, while Philip has nineteen oranges. Find out the person having more oranges.
Solution
Given,
Brian has 15 oranges.
Philip has 19 oranges.
Since 19 is greater than 15, then we write the inequality as19 >15
Therefore, Philip is having more oranges than Brian.
Example 3
A student cut a 20 m rope into two pieces. How is the shorter and longer piece?
Solution
Let the length of the shorter and longer piece be y and x respectively.
S and L must be more than zero meters and their summation should be equal to 20 m.
Write down all the inequalities:
- X > 0
- y > 0
- x < 20
- y < 20
- 0 < x < 20
- 0 < y < 20
- y < x
We now combine the expression:
0 < y < x < 20
x + y = 20 m
These inequalities imply that the shorter length y is more than zero, and the longer length x is more than y, while the longer length is less than the total 20 m. Similarly, the sum of the shorter length y and the longer length x is equivalent to 20 m.

 Solving Greater than Problems
Solving Greater than Problems