Hyperbolic functions – Graphs, Properties, and Examples

The forms of hyperbolic functions (or hyperbolic trigonometric functions) may appear new but their properties are concepts and functions we’ve already encountered in the past. Hyperbolic functions were first studied by mathematicians like Johann Bernoulli to observe the behavior of the curve formed by a hanging chain.

Any object suspended by two points will have exhibit this behavior. This is why hyperbolic functions have extensive applications in physics, engineering, astronomy, and more.

Hyperbolic functions parametrize a hyperbola the same way trigonometric functions parametrize a circle. What makes these functions even more special is that they can be expressed in terms of exponential functions.

In this article, we’ll cover everything we need to know about hyperbolic functions.

• We’ll begin by understanding what these functions represent.
• Learn how to rewrite these six hyperbolic functions as exponential functions.
• Know the different properties and derivative rules applicable to hyperbolic functions.

Why don’t we go ahead and know the six hyperbolic trigonometric functions? Make sure to have a notetaker available, this will be a comprehensive discussion of hyperbolic functions!

What is a hyperbolic function?     

Hyperbolic functions are functions that parametrize a hyperbola. One of the most known examples of an object that can be modeled by a hyperbolic function is a catenary. This is the curve formed when a rope, chain, or cable is suspended.

Mathematicians like Johann Bernoulli have shown us that the curve is not modeled by a parabola, but instead, by the equation, $y = \dfrac{e^x + e^{-x}}{2}$. This equation, is in fact, the hyperbolic cosine function’s equation.

They are used to model behavior similar to one observed from the catenary. We also call these functions hyperbolic trigonometric functions because they’re analogous to trigonometric functions and share similar properties and identities.

These functions: $\boldsymbol{\sinh x}$,$\boldsymbol{\cosh x}$ , $\boldsymbol{\tanh x}$ , and three reciprocal functions are accessible b “hyp” in your calculator. This means that if we can represent $(x, y)$ as $(\sin x, \cos x)$, we can represent $(x, y)$ as $(\sinh x, \cosh x)$ as well.

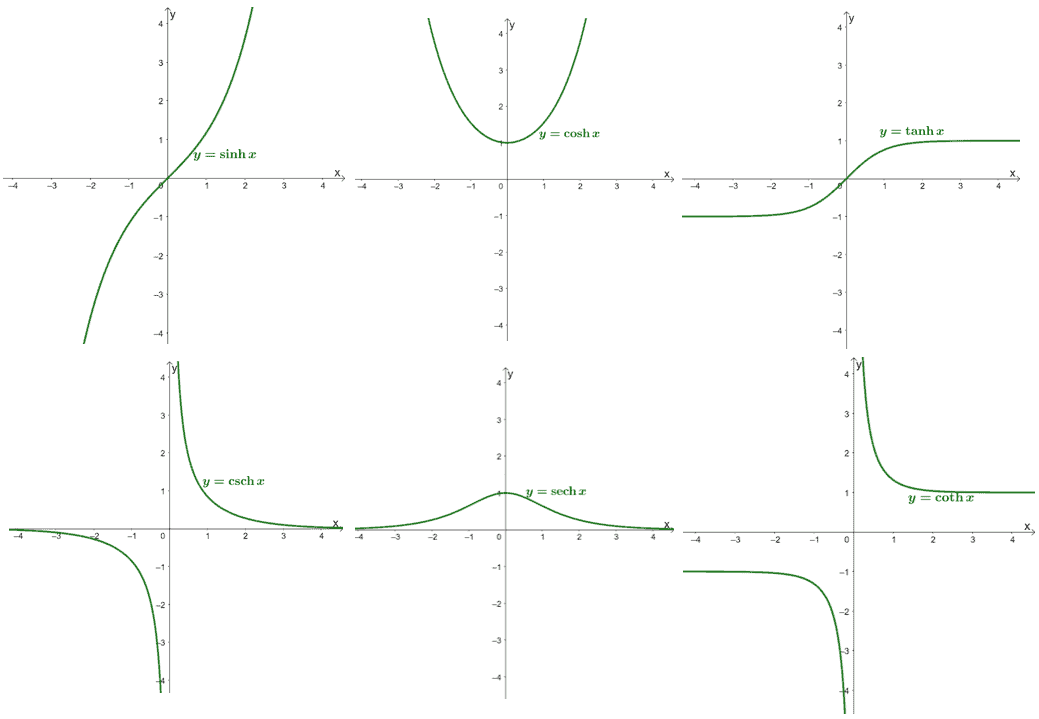
Above are the six graphs of the parent hyperbolic functions. Do these graphs look familiar to you? That’s because hyperbolic functions can be expressed as the sum or difference of two exponential functions.

Definition of hyperbolic function

In math and its further applications, you’ll be encountering $e^x$ and $e^{-x}$ and its many combinations. This is why the hyperbolic functions were established  – to properly label these types of functions. Hyperbolic functions are functions that can be expressed in terms of $\boldsymbol{e^x}$ and $\boldsymbol{e^{-x}}$.

We’ll first observe how the graphs of $\sinh x$ and $\cosh x$ can be formed using $e^x$ and $e^{-x}$.

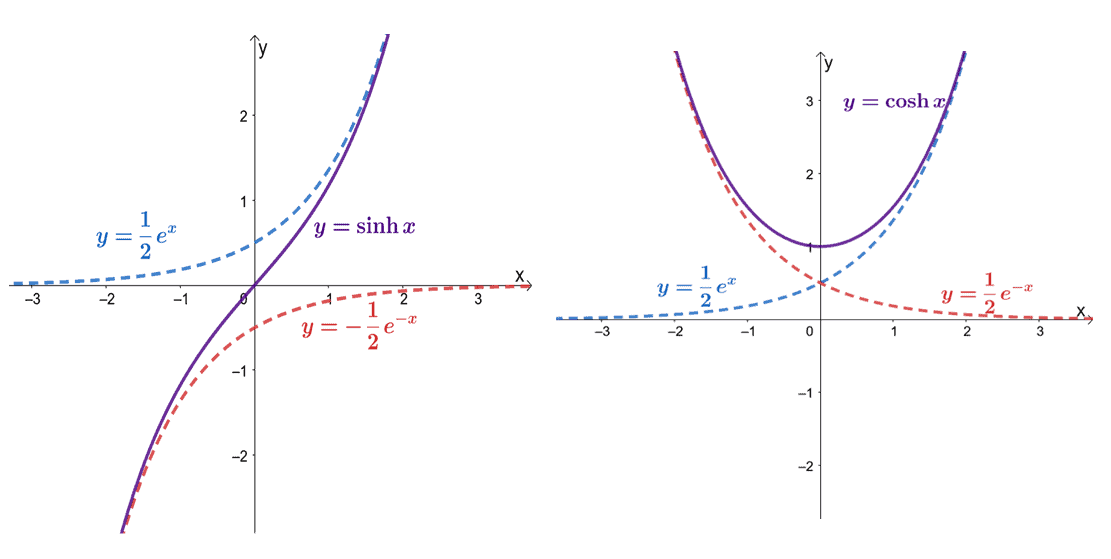
These two graphs show us how $\sinh x$ and $\cosh x$’s graphs were formed using exponential functions.

• We can see that $\sinh x$ is the result of graphically adding the functions, $y =\dfrac{1}{2}e^x$ and $y =-\dfrac{1}{2}e^{-x}$.
• Similarly, we can find the graph of $\cosh x$ by graphically adding the functions, $y = \dfrac{1}{2}e^x$ and $y= \dfrac{1}{2}e^{-x}$.

Hence, we have the following definition for $\sinh x$ and $\cosh x$:

\begin{aligned}\sinh x &= \dfrac{1}{2}e^x – \dfrac{1}{2}e^{-x}\\&=\dfrac{e^x – e^{-x}}{2}\\\cosh x &= \dfrac{1}{2}e^x + \dfrac{1}{2}e^{-x}\\&=\dfrac{e^x + e^{-x}}{2}\end{aligned}

Now that we know the expressions for the hyperbolic sine and cosine, we can apply the quotient identity to find the expression for $\tanh x$:

\begin{aligned}\text{tanh } x &= \dfrac{\sinh x}{\cosh x}\\&=\dfrac{\dfrac{e^x – e^{-x}}{2}}{\dfrac{e^x + e^{-x}}{2}}\\&= \dfrac{e^x – e^{-x}}{e^x + e^{-x}}\end{aligned}

Keep in mind that $\text{tanh } x$ will be undefined when $\cosh x$ is equal to $0$. We can also take the limit of $\dfrac{e^x – e^{-x}}{e^x + e^{-x}}$ as $x$ approaches positive and negative infinity.

\begin{aligned}\lim_{x\rightarrow +\infty} \dfrac{e^x – e^{-x}}{e^x + e^{-x}} &= 1\\ \lim_{x\rightarrow -\infty} \dfrac{e^x – e^{-x}}{e^x + e^{-x}} &= -1\end{aligned}

This means that $\boldsymbol{\tanh x}$ has horizontal asymptotes at $\boldsymbol{y = \pm 1}$. We can find also the expressions for $\text{csch } x$, $\text{sech }x$, and $\coth x$ in terms of $e^x$ and $e^{-x}$ using their corresponding reciprocal identity.

Now that we understand the fundamental definition of hyperbolic functions, let’s go ahead and review the different properties, identities, and rules that apply for these functions.

What are the properties of hyperbolic functions?                

Let’s explore the fundamental properties of hyperbolic functions. We’ll begin by observing the values of $\cosh x$ and $\sinh x$ when $x$ is zero and when $x$ is negative.

Use the exponential form of these two hyperbolic functions to find the values of $\sinh (0)$ and $\cosh x(0)$.

Observe what happens when we evaluate $\sinh (-x)$ and $\cosh (-x)$.

These are fundamental properties of $\sinh x$ and $\cosh x$:

• $\sinh (0) = 0$
• $\cosh (0) = 1$
• $\sinh (-x) = -\cosh x$
• $\cosh (-x) = \sinh x$

As we have mentioned in the earlier section, hyperbolic functions are analogous to trigonometric functions, so it’s best that we check the Pythagorean identities for hyperbolic trigonometric functions.

Recall that for hyperbolic functions, $(x, y) = (\cosh x, \sinh x)$, can be located at the unit hyperbola’s equation, $x^2 – y^2 = 1$.

\begin{aligned}x^2 – y^2 &= 1\\ \cosh^2 x – \sinh^2 &= 1\end{aligned}

We can verify this by substituting $\cosh x$ and $\sinh x$ with their exponential function equivalent.

\begin{aligned}\cosh^2 x – \sinh^2 x &= \left(\dfrac{e^x + e^{-x}}{2} \right )^2-\left(\dfrac{e^x – e^{-x}}{2} \right )^2\\&= \dfrac{(e^{2x} +2\cdot e^x \cdot e^{-x} + e^{-2x})-(e^{2x} -2\cdot e^x \cdot e^{-2x}+ e^{-2x})}{2}\\&=\dfrac{e^{2x}+ 2e^xe^{-x} +e^{2x} – e^{2x} +2e^xe^{-x}- e^{-2x}}{2}\\&= \dfrac{2}{2}\\&= 1\end{aligned}

Apply a similar process to verify the following hyperbolic trigonometric identities:

\begin{aligned}1 – \text{tanh }^2 x &= \text{sech }^2 x\\\text{coth  }^2 x -1 &= \text{csch }^2 x \end{aligned}

Here’s a tip: when verifying identities of hyperbolic functions, use their exponential form then simplify the resulting expressions.

Here are other hyperbolic trigonometric identities we might encounter when working with hyperbolic functions:

What are the derivative rules of hyperbolic functions?                

Use the hyperbolic functions’ exponential expressions to develop their derivative rules. We’ll show you how the rules for $\dfrac{d}{dx} \sinh x$ and $\dfrac{d}{dx} \cosh x$ were established and the rest of the derivative rules will be summarized in a table.

Since $\sinh  x = \dfrac{e^x – e^{-x}}{2}$ and $\cosh  x = \dfrac{e^x + e^{-x}}{2}$, we can use these to establish the derivative rules for $\sinh x$ and $\cosh x$.

Here’s a comprehensive list of the derivative rules for different hyperbolic functions:

Apply a similar approach to confirm the derivative rules of the rest of the hyperbolic functions. Don’t worry, we’ve prepared some examples for you to harness your skills in verifying identities and derivative rules of hyperbolic functions.

Example 1

Given that $f(x) = \cosh x$. Evaluate the values of the following expressions without using a calculator:

a. $f(0)$
b. $f(\ln 2)$
c. $f(-\ln 2)$

Solution

Use exponential form of $\cosh x$, $\sinh x = \dfrac{e^x + e^{-x}}{2}$ to evaluate the three expressions. Substitute $f(x) =  \dfrac{e^x + e^{-x}}{2}$ with $x =0$, $x = \ln 2$, and $x = -\ln 2$.

We’ve summarized the calculations in one table for you.

Hence, we have the following values for $f(x)$:

a. $f(0) = 2$
b. $f(\ln 2) = \dfrac{5}{4}$
c. $f(-\ln 2) = \dfrac{5}{4}$

Example 2

Prove the hyperbolic trigonometric identities that are shown below.

a.$1 – \text{tanh }^2 x= \text{sech }^2x$
b. $\sinh 2x = 2\sinh x \cosh x$
c. $\cosh (M + N) = \cosh M \cosh N + \sinh M \sinh N$

Solution

Let’s focus on rewriting $1 – \text{tanh }^2 x$ to $\text{sech }^2 x$. Begin by using the exponential form of $\tanh x = \dfrac{e^x – e^{-x}}{e^x + e^{-x}}$ to rewrite the left-hand side expression of the first equation.

\begin{aligned}1 – \text{tanh }^2 x &= 1 – \left(\dfrac{e^x – e^{-x}}{e^x + e^{-x}} \right )^2\\&=1 – \left(\dfrac{e^{2x} – 2e^{-x}e^x + e^{-2x}}{e^{2x} + 2e^{-x}e^x + e^{-2x}} \right )\\&=1 – \left(\dfrac{e^{2x} – 2 + e^{-2x}}{e^{2x} + 2 + e^{-2x}} \right )\\&=\left(\dfrac{e^{2x} + 2 + e^{-2x}}{e^{2x} + 2 + e^{-2x}} \right ) – \left(\dfrac{e^{2x} – 2 + e^{-2x}}{e^{2x} + 2 + e^{-2x}} \right )\\&= \dfrac{e^{2x} + 2 + e^{-2x}-e^{2x} + 2 – e^{-2x}}{e^{2x} + 2 + e^{-2x}}\\&= \dfrac{4}{e^{2x} + 2 + e^{-2x}}   \end{aligned}

Express the denominator as the square of $(e^x + e^{-x})$ then use the exponential form of $\text{sech }x = \dfrac{2}{e^x + e^{-x}}$ to rewrite the resulting expression.

\begin{aligned}1 – \text{tanh }^2 x &= \dfrac{4}{(e^{x} + e^{-x})^2}\\&= \left( \dfrac{2}{e^{x} + e^{-x}}\right )^2\\&= (\text{sech }x)^2\\&= \text{sech }^2x  \end{aligned}

a. Hence, we’ve shown that $1 – \text{tanh }^2 x= \text{sech }^2x$.

Moving on to the second identity, we’ll start by using the exponential form of $\sinh x$ and $\cosh x$ to rewrite the right-hand side of the equation.

\begin{aligned}2\sinh x \cosh x &= 2\left(\dfrac{e^{x} – e^{-x}}{2} \right )\left(\dfrac{e^{x} + e^{-x}}{2} \right )\\&= 2\left(\dfrac{e^{2x} – e^{-2x}}{4} \right ),\phantom{x}\color{Teal}(a-b)(a +b) = a^2 -b^2 \\&= \dfrac{e^{2x} – e^{-2x}}{2}\\&= \sinh 2x\end{aligned}

b. This confirms that $\sinh 2x = 2\sinh x \cosh x$.

For the third identity, let’s manipulate the right-hand side of the expression. Again, we use the exponential forms of $\sinh M$, $\cosh M$, $\sinh N$, and $\cosh N$ to rewrite the expression. Begin by simplifying $\cosh M \cosh N$ and $\sinh M \sinh N$ first separately.

Simplify the sum of $\cosh M \cosh N$ and $\sinh M \sinh N  $ further to come up with the left-hand side of the identity.

\begin{aligned}\cosh M \cosh N + \sinh M \sinh N  &=  \dfrac{e^Me^N  + e^{-M}e^{-N}}{2}\\&=\dfrac{e^{M + N} + e^{-(M + N)}}{2}\\&= \cosh(M + N) \end{aligned}

c. Therefore, $\cosh (M + N) = \cosh M \cosh N + \sinh M \sinh N$.

Example 3

Evaluate the derivative of the following hyperbolic functions:

a. $\dfrac{d}{dx} \cosh (x – n)$
b. $\dfrac{d}{dx} \tanh (\ln x)$

Solution

Use the derivative rule for $\cosh x$ and apply the chain rule to differentiate $\cosh(x –n)$ as shown below.

\begin{aligned}\dfrac{d}{dx} \cosh (x – n) &= {\color{Teal}\sinh(x -n)} \cdot {\color{Orchid}\dfrac{d}{dx}(x -n)},\phantom{x}{\color{Teal}\dfrac{d}{dx}\cosh x=\sinh x}\text{ & }{\color{Orchid}\text{Chain Rule}}\\&= \sinh (x -n)\cdot \left({\color{Teal}\dfrac{d}{dx}x – \dfrac{d}{dx}n}\right),\phantom{x}{\color{Teal}\text{Difference Rule}}\\&= \sinh (x -n)\cdot ({\color{Teal}1} – {\color{Orchid}0}),\phantom{x}{\color{Teal}\text{Power Rule}}\text{ & }{\color{Orchid}\text{Constant Rule}}\\&=\sinh (x -n) \end{aligned}

a. This means that $\dfrac{d}{dx} \cosh (x – n) = \sinh (x –n)$.

Apply the derivative rule, $\dfrac{d}{dx} \tanh x = \text{sech }^2 x$ to differentiate the second expression. Make sure to apply the chain rule for the inner function.

\begin{aligned}\dfrac{d}{dx} \tanh(\ln x) &= {\color{Teal}\text{sech }^2x(\ln x)} \cdot {\color{Orchid}\dfrac{d}{dx}(\ln x)},\phantom{x}{\color{Teal}\dfrac{d}{dx}\tanh x=\text{sech }^2x}\text{ & }{\color{Orchid}\text{Chain Rule}}\\&= \text{sech }^2(\ln x)\cdot \left({\color{Teal}\dfrac{1}{x}}\right),\phantom{x}{\color{Teal}\dfrac{d}{dx}\ln x = \dfrac{1}{x}}\\&= \dfrac{1}{x}\text{sech }^2{(\ln x)} \end{aligned}

Simplify $\text{sech }^2(\ln x)$ further by using the exponential form of $\text{sech }x$.

\begin{aligned}\dfrac{1}{x}\text{sech }^2{(\ln x)} &= \dfrac{1}{x}\cdot\left(\dfrac{2}{e^{\ln x} + e^{-\ln x}} \right )^2\\&=\dfrac{1}{x}\cdot\left(\dfrac{2}{{\color{Teal} x} + {\color{Teal} \dfrac{1}{x}} } \right )^2 ,\phantom{x}\color{Teal} e^{\ln a} =a\\&= \dfrac{1}{x}\left(\dfrac{2}{\dfrac{x^2 + 1}{x}} \right )^2\\&= \dfrac{4x}{(x^2 + 1)^2}\end{aligned}

b. Hence, we’ve shown that $\dfrac{d}{dx} \tanh (\ln x)$ is equal to $\dfrac{1}{x}\text{sech }^2 (\ln x)$ or $\dfrac{4x}{(x^2 + 1)^2}$.

Example 4

Let’s say we have $\sinh x = \dfrac{5}{13}$, what are the exact values of $x$ that satisfy the equation?

Solution

Find the value of $\cosh x$ using the identity, $\cosh^2 x =1 + \sinh^2x$, and the fact that $\sinh x = \dfrac{5}{12}$.

\begin{aligned}\cosh^2 x =1 + \sinh^2 x\\\cosh^2 x &= 1 + \left(\dfrac{5}{12}\right)^2 \\\cosh^2 x&= \dfrac{169}{144}\\\cosh x &= \pm \dfrac{13}{12}\end{aligned}

Since $\cosh x$ is always positive, we’ll use $\cosh x = \dfrac{13}{12}$. Now, let’s observe what happens when we add $\sinh x$ and $\cosh x$.

\begin{aligned}\sinh x &= \dfrac{e^x – e^{-x}}{2}\\\cosh x &= \dfrac{e^x + e^{-x}}{2}\\\\\sinh x + \cosh x &= \dfrac{2e^x}{2}\\&= e^x\end{aligned}

This means that $\dfrac{5}{12} + \dfrac{13}{12} = e^x$. Simplify the right-hand side then take the natural logarithm of both sides of the equation to find $x$.

\begin{aligned}\dfrac{18}{12}&= e^x\\\ln\left(\dfrac{3}{2}\right )&= \ln(e^x),\phantom{x}{\color{Teal}\ln(e^a) =a}\\x&= \ln\left(\dfrac{3}{2} \right )\end{aligned}

This means that the exact value of $x$ is $\ln\left(\dfrac{3}{2}\right)$.

Practice Questions

1. Given that $f(x) = \sinh x$. Evaluate the values of the following expressions without using a calculator:
a. $f(0)$
b. $f(\ln 4)$
c. $f(-\ln 4)$
2. Given that $g(x) = \tanh x$. Evaluate the values of the following expressions without using a calculator:
a. $f(0)$
b. $f(\ln 5)$
c. $f(-\ln 5)$
3. Prove the hyperbolic trigonometric identities that are shown below.
a.$\cosh 2x = 2\cosh^2 x -1$
b. $\sinh (M – N) = \sinh M \cosh N – \sinh N \cosh M$
4. Show that $\dfrac{d}{dx} \text{tanh }x = \text{sech }^2 x$.
5. Evaluate the derivative of the following hyperbolic functions:
a. $\dfrac{d}{dx} \tanh (x – n)$
b. $\dfrac{d}{dx} \cosh (\ln x)$
c. $\dfrac{d}{dx} 3x^2 \sinh x$
6. Let’s say we have $\cosh x = \dfrac{41}{40}$, what are the exact values of $x$ that satisfy the equation?

Answer Key

1.
a.$f(0) =0$
b. $f(\ln 4) = \dfrac{15}{8}$
c. $f(-\ln 4) =- \dfrac{15}{8}$
2.
a.$g(0) =0$
b. $g(\ln 5) = \dfrac{12}{13}$
c. $g(-\ln 5) =- \dfrac{12}{13}$
3.
a.
$\begin{aligned}2\cosh^2 x -1&= 2\left(\dfrac{e^x + e^{-x}}{2} \right )^2- 1\\&= \dfrac{e^{2x} +2 + e^{-2x}}{2}-1\\&=\dfrac{e^{2x} +2+ e^{-2x} -2}{2}\\&= \dfrac{e^{2x} + e^{-2x}}{2}\\&= \cosh 2x\end{aligned}$
b.
$\begin{aligned}\sinh M \cosh N &= \left(\dfrac{e^M – e^{-M}}{2} \right )\left(\dfrac{e^N + e^{-N}}{2} \right )\\&=\dfrac{e^M e^N +e^M e^{-N}-e^{-M}e^N -e^{-M}e^{-N}}{4} \\ \sinh N \cosh M&= \left(\dfrac{e^N – e^{-N}}{2} \right )\left(\dfrac{e^M + e^{-M}}{2} \right )\\&=\dfrac{e^M e^N +e^N e^{-M}-e^{M}e^{-N} -e^{-M}e^{-N}}{4}\\\\\sinh M \cosh N-\sinh N \cosh&= \dfrac{2e^{M -N} + 2e^{-(M -N)}}{4}\&= \dfrac{e^{M -N} – e^{-(M-N)}}{2}\\&= \sinh (M -N)\end{aligned}$
4.
$\begin{aligned}\dfrac{d}{dx} \text{tanh }x &= \dfrac{d}{dx}\left(\dfrac{e^x-e^{-x}}{e^x + e^{-x}}\right)\\&= \dfrac{(e^x + e^{-x})\dfrac{d}{dx}(e^x-e^{-x})-(e^x – e^{-x})\dfrac{d}{dx}(e^x+e^{-x})}{(e^x + e^{-x})^2}\\&= \dfrac{(e^x + e^{-x})(e^x + e^{-x})-(e^x – e^{-x})(e^x – e^{-x})}{(e^x + e^{-x})^2}\\&= \dfrac{4}{(e^x + e^{-x})^2}\\&= \left(\dfrac{2}{e^x + e^{-x}}\right)^2\\&=\text{sech }^2x\end{aligned}$
5.
a. $\dfrac{d}{dx} \tanh (x – n) = \text{sech }^2 (x –n)$
b. $\dfrac{d}{dx} \cosh (\ln x) = \dfrac{1}{x} \sinh(\ln x)= \dfrac{x^2 -1}{2x} $
c. $\dfrac{d}{dx} 3x^2 \sinh x = 3(2x \sinh x + x^2 \cosh x)$
6. $x = \ln\left(\dfrac{5}{4}\right)$

Images/mathematical drawings are created with GeoGebra.