Improper Integrals – Definition, Types, and Examples

Improper integrals are special cases of definite integrals. What makes improper integrals unique are their lower and upper limits. In the past, we’ve worked on definite integrals within a finite interval, but this time, we’ll see what happens when we evaluate a definite integral with $\boldsymbol{\infty}$ found at its lower or/and upper limits.

Improper integrals are definite integrals with one or both ends of the intervals contain either $\boldsymbol{-\infty}$ or $\boldsymbol{\infty}$.  Improper integral converges when the evaluated integral returns a finite value. Otherwise, the improper integral is divergent.

Our discussion will include conditions for improper integrals and the techniques we’ll need to evaluate improper integrals. We’ll also cover examples of improper integrals that are divergent and convergent.

Since definite and improper integrals are closely related, review your notes on definite integrals as defined by the fundamental theorem of calculus.  For now, let’s go ahead and understand the components that make up an improper integral.

What is an improper integral?

Improper integrals are definite integrals where either one or two of the limits of the integration are infinite or the integrand is infinite. In the past, we’ve learned about definite integrals,$\int_{a}^{b} f(x)\phantom{x} dx$, where $a$ and $b$ are finite and the integrand, $f(x)$, are bounded. But what if our given definite integral does meet those conditions? This is when improper integrals come in handy.

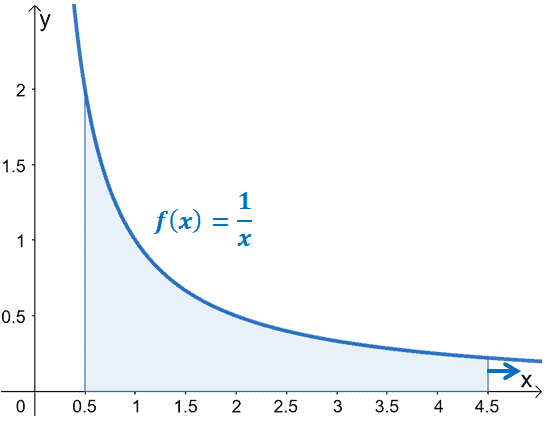
 The graph above, particularly the area under the curve of $f(x)$, can be represented by the improper integral, $\int_{0.5}^{\infty} \dfrac{1}{x}\phantom{x}dx$.

Improper integrals are integrals that 1) contain infinite limit for integration or 2) has an unbounded integral. Below are three other examples of improper integrals:

• The first integral contains $\infty$ as its upper limit. In fact, this improper integral converges to $\dfrac{\pi}{4}$.
• The second integral has $\pm \infty$ in its lower and upper limits. This improper integral diverges.
• The third example does not contain $\pm \infty$ in both its lower and upper limits, but the integrand is undefined when $x =2$ which is within the interval. In fact, the improper integral also diverges.

We’ll explore more about evaluating improper integrals in the next few sections, but for now, let’s go ahead and review the conditions required of an improper integral.

How to tell if an integral is improper?

When given a definite integral, $\int_{a}^{b} f(x) \phantom{x} dx$, we can tell that it is improper when it satisfies one or both conditions:

1. i) Either or both ends of the interval, $[a, b]$, are infinite.
2. ii) The integrand, $f(x)$, is not bounded within the given interval, $[a, b]$.

In this discussion, we’ll focus on the three types of improper integrals we’ll encounter:

• Improper integrals that contain one infinite limit in their expressions.
• Improper integrals that contain two infinite limits in their expressions.
• Improper integrals that discontinuities within its interval.

Improper integral’s formal definition and condition

Let’s begin by understanding the conditions when the improper integral only has one positive or negative infinite limit in its expression.

Improper integrals – one infinite limit:

This means that when $f(x)$ is continuous within the interval, $[a, \infty)$, there exists an improper integral for $f(x)$ over $[a, \infty)$. Similarly, when $f(x)$ is continuous over the interval, $(-\infty, b]$, we can evaluate an improper integral for $f(x)$ throughout the interval.

The limits on the right-hand side of the equation will guide us in determining whether the given improper integral is divergent or convergent:

• When the limit exists and returns a finite value, the improper integral is said to be convergent.
• When the limit is either $\boldsymbol{\pm \infty}$ or does not exist, the improper integral is divergent.

This means that the improper integrals with one infinite limit can be evaluated by replacing the infinite limit with $\boldsymbol{N}$ then finding the definite integral’s limit as $\boldsymbol{N \rightarrow \pm \infty}$.

Improper integrals – two infinite limits:

Another type of improper integrals are definite integrals, $\int_{a}^{b} f(x)\phantom{x}dx$, where both $a$ and $b$ are either $-\infty$ and $\infty$.

This equation shows us how to evaluate improper integrals by breaking down the improper integral into two improper integrals with only one infinite limit.

• When both $\int_{-\infty}^{a} f(x)\phantom{x}dx$ and $\int_{a}^{\infty} f(x)\phantom{x}dx$ are convergent, $\int_{-\infty}^{\infty} f(x) \phantom{x}$ will also be convergent.
• If either $\int_{-\infty}^{a} f(x)\phantom{x}dx$ or $\int_{a}^{\infty} f(x)\phantom{x}dx$ is divergent, our improper integral with two infinite limits will also be divergent.

Improper integrals – discontinuities:

There are instances when improper integrals don’t contain any infinite limits. Definite integrals are improper when the integrand’s discontinuity is located within the interval or are at the interval’s endpoint.

Let’s focus on improper integrals where the discontinuity of the integrand is found in either the lower or upper limit.

Hence, if $f(x)$ is continuous within the interval, $(a, b]$, there exists an improper integral for $f(x)$ over $(a, b]$. In addition, when $f(x)$ is continuous over the interval, $(a, b]$, there exists an improper integral for $f(x)$ over the given interval. To evaluate improper integrals like this, take the limit as $\boldsymbol{N \rightarrow a+}$ or $\boldsymbol{N \rightarrow b}$, depending on where the discontinuity is located.

There are also instances when the discontinuity of the integrand is actually located within the interval. For example, if $x =c$ is a discontinuity of $f(x)$ and $c \in [a, b]$, we have the improper integral shown below:

This shows that when both definite integrals, $\boldsymbol{\int_{a}^{c} f(x)\phantom{x}dx}$ and $\boldsymbol{\int_{c}^{b} f(x)\phantom{x}dx}$, are convergent, the improper integral is also convergent.

How to solve improper integrals?

Use the definition and conditions for improper integrals when evaluating them. Here are some pointers to remember when solving problems involving improper integrals:

• Confirm if the definite integral is indeed an improper integral.
• Identify whether the improper integral is divergent or convergent.
• Apply appropriate techniques to evaluate the improper integral.

For example, try checking whether the area of bounded by the curve of $f(x) = \dfrac{1}{x}$, the $x$-axis and the interval, $[+1, \infty)$ is finite or infinite. Use the techniques we’ve learned to determine the nature of improper integral by evaluating the improper integral, $\int_{1}^{\infty} \dfrac{1}{x}\phantom{x}dx$.

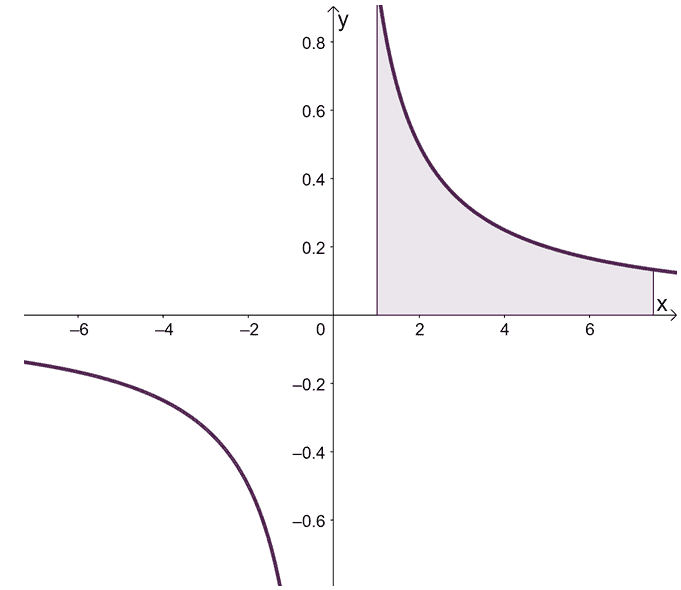
Here’s the graph of the curve along with the area representing the improper integral, $\int_{1}^{\infty} \dfrac{1}{x}\phantom{x}dx$. This improper integral has one infinite limit at its upper bound, so we apply the following steps:

• Replace the upper limit with $N$.
• Evaluate the definite integral using the property, $\int \dfrac{1}{x} \phantom{x}dx = \ln|x| + C$ while treating $N$ as a constant.
• Take the limit of $N$ as it approaches $\infty$.

\begin{aligned} \int_{1}^{\infty} \dfrac{1}{x}\phantom{x}dx &= \lim_{N\rightarrow \infty}\int_{1}^{N} \dfrac{1}{x}\phantom{x}dx\\&= \lim_{N \rightarrow \infty}[\ln |x|]_{1}^{N}\\&= \lim_{N \rightarrow \infty} (\ln |N| – \ln|1|)\\&= \lim_{N \rightarrow \infty} (\ln |N| -0)\\&=  \infty \end{aligned}

This shows that the area bounded by the curve, the $x$-axis, and the interval, $[1, \infty)$, is infinite and diverges.

Example 1

Evaluate the improper integral, $\int_{0}^{\infty} \dfrac{1}{x^2 + 9}\phantom{x}dx$. Determine whether the integral converges or diverges.

Solution

The integral is improper with an infinite upper limit, so we can evaluate this integral by rewriting it using the property, $\int_{a}^{\infty} f(x) \phantom{x}dx = \lim_{N \rightarrow \infty} \int_{a}^{N} f(x)\phantom{x}dx$, as guide.

\begin{aligned} \int_{0}^{\infty} \dfrac{1}{x^2 + 9} &=\lim_{N \rightarrow \infty} \int_{0}^{N} \dfrac{1}{x^2 + 9} \phantom{x}dx\end{aligned}

Use the andtiderivative formula, $\int \dfrac{1}{x^2 + a^2} = \dfrac{1}{a} \tan^{-1}\left(\dfrac{x}{a}\right) + C$, to evaluate the definite integral.

\begin{aligned} \lim_{N \rightarrow \infty} \int_{0}^{N} \dfrac{1}{x^2 + 9}\phantom{x}dx &=\lim_{N \rightarrow \infty} \left[\dfrac{1}{3} \tan^{-1}\left(\dfrac{x}{3}\right)\right]_{0}^{N}\\&= \lim_{N \rightarrow \infty} \left[ \dfrac{1}{3} \tan^{-1}\left(\dfrac{N}{3}\right) -\dfrac{1}{3} \tan^{-1}\left(\dfrac{0}{3}\right)\right ]\\&=  \lim_{N \rightarrow \infty} \dfrac{1}{3}\tan^{-1}\left(\dfrac{N}{3} \right )\end{aligned}

Remember that tangent is undefined or infinite when cosine is zero. This means that $\tan ^{-1} \infty = \dfrac{\pi}{2}$.

\begin{aligned} \lim_{N \rightarrow \infty} \dfrac{1}{3}\tan^{-1}\left(\dfrac{N}{3} \right )&= \dfrac{1}{3}\tan^{-1} \infty\\&= \dfrac{1}{3}\cdot \dfrac{\pi}{2}\\ &=\dfrac{\pi}{6}\end{aligned}

This means that the improper integral is convergent and in fact, $\int_{0}^{\infty} \dfrac{1}{x^2 + 9}\phantom{x}dx = \dfrac{\pi}{6}$.

Example 2

Determine the value of $p$ when the improper integral, $\int_{1}^{\infty} \dfrac{1}{x^p}\phantom{x} dx$, are convergent and divergent. Keep in mind that $p >0$ and $p \neq 1$.

Solution

Rewrite $\int_{1}^{\infty} \dfrac{1}{x^p}\phantom{x} dx$ as $\lim_{N \rightarrow \infty} \int_{1}^{N} \dfrac{1}{x^p}\phantom{x}dx$. Express $\dfrac{1}{x^p}$ as $x^{-p}$ then use the power rule, $\int x^n\phantom{x}dx = \dfrac{x^{n + 1}}{n  + 1} + C$, to evaluate the improper integral.

\begin{aligned} \int_{1}^{\infty} \dfrac{1}{x^p}\phantom{x} dx & = \lim_{N \rightarrow \infty} \int_{1}^{N} \dfrac{1}{x^p}\phantom{x}dx\\ &=\lim_{N \rightarrow \infty} \int_{1}^{N} x^{-p} \phantom{x}dx\\&= \lim_{N \rightarrow \infty} \left[\dfrac{x^{-p + 1}}{-p + 1} \right ]_{1}^{N}\end{aligned}

Factor out $\dfrac{1}{1 –p}$ then simplify the remaining limit expression.

\begin{aligned} \lim_{N \rightarrow \infty} \left[\dfrac{x^{-p + 1}}{-p + 1} \right ]_{1}^{N}&= \dfrac{1}{1 – p}\lim_{N \rightarrow \infty} \left[x^{-p + 1} \right ]_{1}^{N}\\ &= \dfrac{1}{1 – p}\lim_{N \rightarrow \infty} \left(N^{-p + 1} – 1^{-p + 1}\right)\\ &= \dfrac{1}{1 – p}\lim_{N \rightarrow \infty} \left(N^{-p + 1} – 1\right)\\ &= \dfrac{1}{p -1}\lim_{N \rightarrow \infty} \left(1 -N^{1- p}\right)\end{aligned}

Let’s now observe the two possible cases: when $p$ is a fraction or when $p$ is a whole number.

• When $0 < p<1$, $N^{1 –p} \rightarrow \infty$ as $N \rightarrow \infty$. Meaning, the improper integral diverges.
• When $p > 1$, $N^{1 –p} = \dfrac{1}{N^{p – 1}}$ as $N \rightarrow \infty$. Hence, the improper integral converges.

This means that $\int_{1}^{\infty} \dfrac{1}{x^p}\phantom{x} dx$ is convergent when $p >1$ and divergent when $0 < p <1$.

Example 3

Evaluate the improper integral, $\int_{-3}^{3} \dfrac{1}{x^4}\phantom{x}dx$. Determine whether the integral converges or diverges.

Solution

The integrand has a discontinuity at $x =0$ and is within the interval, $[-3, 3]$. Rewrite the improper integral as a sum of two definite integrals with $0$ as the lower limit and upper limit for the first and second definite integral.

\begin{aligned}\int_{-3}^{3} \dfrac{1}{x^4}\phantom{x}dx &= \int_{-3}^{0} \dfrac{1}{x^4}\phantom{x}dx + \int_{0}^{3} \dfrac{1}{x^4}\phantom{x}dx\end{aligned}

Now that we have $0$ as one lower and upper bounds of the intervals, use the property for improper integrals with discontinuities.

\begin{aligned} \int_{-3}^{0} \dfrac{1}{x^4} \phantom{x}dx &= \lim_{N \rightarrow 0} \int_{-3}^{N} f(x)\phantom{x}dx\\\int_{0}^{3} \dfrac{1}{x^4} \phantom{x}dx &= \lim_{N \rightarrow 0+} \int_{N}^{3} f(x)\phantom{x}dx\\\\\int_{-3}^{0} \dfrac{1}{x^4}\phantom{x}dx + \int_{0}^{3} \dfrac{1}{x^4}\phantom{x}dx &= \lim_{N \rightarrow 0} \int_{-3}^{N} f(x)\phantom{x}dx + \lim_{N \rightarrow 0+} \int_{N}^{3} f(x)\phantom{x}dx\end{aligned}

Simplify the resulting expression and evaluate the limits.

\begin{aligned}\lim_{N \rightarrow 0+} \int_{-3}^{N} \dfrac{1}{x^4}\phantom{x}dx + \lim_{N \rightarrow 0+} \int_{N}^{3} \dfrac{1}{x^4}\phantom{x}dx &=\lim_{N \rightarrow 0+} \int_{-3}^{N} x^{-4}\phantom{x}dx + \lim_{N \rightarrow 0+} \int_{N}^{3} x^{-4}\phantom{x}dx\\&=\lim_{N \rightarrow 0+} \left[\dfrac{x^{-4 + 1}}{-4+ 1} \right ]_{-3}^N +\lim_{N \rightarrow 0+} \left[\dfrac{x^{-4 + 1}}{-4+ 1} \right ]_{N}^3\\&=\lim_{N \rightarrow 0+} \left[\dfrac{x^{-3}}{-3} \right ]_{-3}^N +\lim_{N \rightarrow 0+} \left[\dfrac{x^{-3}}{-3} \right ]_{N}^3\\&=\lim_{N \rightarrow 0+} \left[\dfrac{N^{-3}}{-3} – \dfrac{-3^{-3}}{-3}\right ] + \lim_{N \rightarrow 0+} \left[\dfrac{N^{-3}}{-3} – \dfrac{3^{-3}}{-3}\right ]\\&= \lim_{N \rightarrow 0+}\dfrac{-6}{2N^3}\\&= \infty\end{aligned}

Since $\int_{-3}^{3} \dfrac{1}{x^4}\phantom{x}dx = infty$, the improper integral diverges.

Example 4

Show that $\int_{1}^{\infty} \dfrac{\cos^2 x}{x^2} \phantom{x}dx$ converges.

Solution

Before we work on proving that $\int_{1}^{\infty} \dfrac{\cos^2 x}{x^2} \phantom{x}dx$ is indeed convergent, let’s recall the comparison property:

• When $f(x) \geq g(x) \geq 0$ and $\int_{a}^{\infty} f(x)\phantom{x}dx$ is convergent, $\int_{a}^{\infty} g(x)\phantom{x}dx$ is convergent as well.
• When $f(x) \geq g(x) \geq 0$ and $\int_{a}^{\infty} f(x)\phantom{x}dx$ is divergent, $\int_{a}^{\infty} g(x)\phantom{x}dx$ is also divergent.

Let’s begin with the fact that $0 \leq \cos^2 x \leq 1$. Divide both sides of the inequality by $x^2$. Since $x^2$ will always be positive, the inequalities won’t change.

\begin{aligned}0 &\leq \cos^2 x \leq 1\\0 &\leq \dfrac{\cos^2 x }{x^2}\leq \dfrac{1}{x^2}\end{aligned}

We’ve shown that $\dfrac{1}{x^2} \geq \cos^2 x \geq 0$. Using our results from Example 2, $\int_{1}^{\infty} \dfrac{1}{x^2}\phantom{x} dx$ is convergent since $\int_{1}^{\infty} \dfrac{1}{x^p} \phantom{x}dx$ is convergent when $p >1$.

Through comparison test, we can conclude that since           $\dfrac{1}{x^2} \geq \cos^2 x \geq 0$ and $\int_{1}^{\infty} \dfrac{1}{x^2}\phantom{x} dx$ is convergent, $\int_{1}^{\infty} \dfrac{\cos^2 x}{x^2}\phantom{x}dx$ is convergent as well.

Practice Questions

1. Evaluate the improper integral, $\int_{0}^{\infty} \dfrac{1}{x^2 + 4}\phantom{x}dx$. Determine whether the integral converges or diverges.

2. Determine whether the improper integrals shown below are divergent or convergent.
a. $\int_{1}^{\infty} \dfrac{1}{x^3}\phantom{x} dx$
b. $\int_{1}^{\infty} \dfrac{1}{x^{\frac{1}{2}}}\phantom{x} dx$
c. $\int_{1}^{\infty} \dfrac{1}{\sqrt[4]{x}}\phantom{x} dx$
d. $\int_{1}^{\infty} \dfrac{1}{x^6}\phantom{x} dx$

3. Evaluate the improper integral, $\int_{-4}^{4} \dfrac{1}{x^2 -4 }\phantom{x}dx$. Determine whether the integral converges or diverges.

4. Show that $\int_{1}^{\infty} \dfrac{1}{xe^x} \phantom{x}dx$ converges.

Answer Key

1. $\int_{0}^{\infty} \dfrac{1}{x^2 + 4}\phantom{x}dx = \dfrac{\pi}{4}$; Integral converges.
2.
a. Convergent
b. Divergent
c. Divergent
d. Convergent
3. $\int_{-4}^{4} \dfrac{1}{x^2 -4 }\phantom{x}dx$ diverges
4.
$\begin{aligned}0 &\leq \dfrac{1}{xe^x} \leq \dfrac{1}{e^x}\\\\\int_{1}^{\infty} \dfrac{1}{e^x} \phantom{x}dx &=\int_{1}^{\infty} e^{-x} \phantom{x}dx\\&= \lim_{N \rightarrow \infty} \int_{1}^{N} e^{-x}\phantom{x}dx\\&= \lim_{N \rightarrow \infty} \left[e^{-N} + e^{1} \right ]\\&= e\end{aligned}$
Since $0 \leq \dfrac{1}{xe^x} \leq \dfrac{1}{e^x}$ and $\int_{1}^{\infty} \dfrac{1}{e^x} \phantom{x}dx$ is convergent, $\int_{1}^{\infty} \dfrac{1}{xe^x} \phantom{x}dx$ is also convergent.

Images/mathematical drawings are created with GeoGebra.