The Inscribed Angle Theorem – Explanation & Examples

The circular geometry is really vast. A circle consists of many parts and angles. These parts and angles are mutually supported by certain Theorems, e.g., the Inscribed Angle Theorem, Thales’ Theorem, and Alternate Segment Theorem.

We will go through the inscribed angle theorem, but before that, let’s have a brief overview of circles and their parts.

Circles are all around us in our world. There exists an interesting relationship among the angles of a circle. To recall, a chord of a circle is the straight line that joins two points on a circle’s circumference. Three types of angles are formed inside a circle when two chords meet at a common point known as a vertex. These angles are the central angle, intercepted arc, and the inscribed angle.

For more definitions related to circles, you need to go through the previous articles.

In this article, you will learn:

• The inscribed angle and inscribed angle theorem,
• we will also learn how to prove the inscribed angle theorem.

What is the Inscribed Angle?

An inscribed angle is an angle whose vertex lies on a circle, and its two sides are chords of the same circle.

On the other hand, a central angle is an angle whose vertex lies at the center of a circle, and its two radii are the sides of the angle.

The intercepted arc is an angle formed by the ends of two chords on a circle’s circumference.

Let’s take a look.

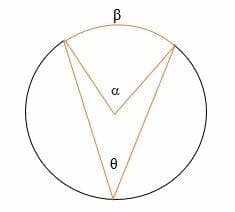
In the above illustration,

α = The central angle

θ = The inscribed angle

β = the intercepted arc.

What is the Inscribed Angle Theorem?

The inscribed angle theorem, which is also known as the arrow theorem or the central angle theorem, states that:

The size of the central angle is equal to twice the size of the inscribed angle. The inscribed angle theorem can also be stated as:

• α = 2θ

The size of an inscribed angle is equal to half the size of the central angle.

• θ = ½ α

Where α and θ are the central angle and inscribed angle, respectively.

How do you Prove the Inscribed Angle Theorem?

The inscribed angle theorem can be proved by considering three cases, namely:

• When the inscribed angle is between a chord and the diameter of a circle.
• The diameter is between the rays of the inscribed angle.
• The diameter is outside the rays of the inscribed angle.

Case 1: When the inscribed angle is between a chord and the diameter of a circle:

To prove α = 2θ:

• △ CBD is an isosceles triangle whereby CD = CB = the radius of the circle.
• Therefore, ∠ CDB = ∠ DBC = inscribed angle = θ
• The diameter AD is a straight line, so ∠BCD = (180 – α) °
• By triangle sum theorem, ∠CDB + ∠DBC + ∠BCD = 180°

θ + θ + (180 – α) = 180°

Simplify.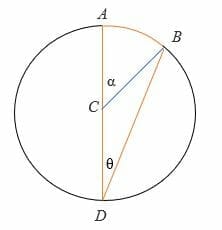

⟹ θ + θ + 180 – α = 180°

⟹ 2θ + 180 – α = 180°

Subtract 180 on both sides.

⟹ 2θ + 180 – α = 180°

⟹ 2θ – α = 0

⟹ 2θ = α. Hence proved.

Case 2: when the diameter is between the rays of the inscribed angle.

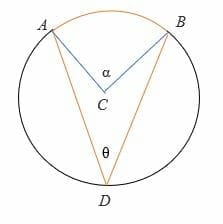
To prove 2θ = α:

• First, draw the diameter (in dotted line) of the circle.

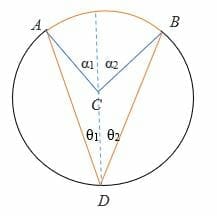
• Let the diameter bisects θ into θ₁ and θ Similarly, the diameter bisects α into α₁ and α₂.

⟹ θ₁ + θ₂ = θ

⟹ α₁ + α₂ = α

• From the first case above, we already know that,

⟹ 2θ₁ = α₁

⟹ 2θ₂ = α₂

• Add the angles.

⟹ α₁ + α₂ = 2θ₁ + 2θ₂

⟹ α₁ + α₂ = 2 (θ₁ + 2θ₂)

Hence, 2θ = α:

Case 3: When the diameter is outside the rays of the inscribed angle.

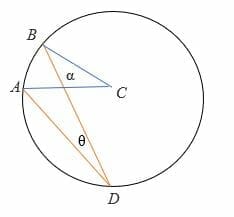
To prove 2θ = α:

• Draw the diameter (in dotted line) of the circle.

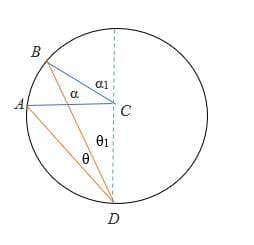
• Since 2θ₁= α₁

⟹ 2 (θ₁ + θ) = α + α₁

⟹ But, 2θ₁ = α₁ and 2θ₂ = α₂

⟹ By substitution, we get,

2θ = α:

Solved examples about inscribed angle theorem

Example 1

Find the missing angle x in the diagram below.

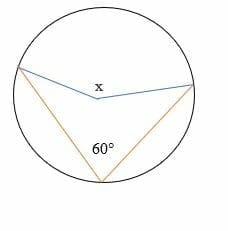
Solution

By inscribed angle theorem,

The size of the central angle = 2 x the size of the inscribed angle.

Given, 60° = inscribed angle.

Substitute.

The size of the central angle = 2 x 60°

= 120°

Example 2

Given that ∠QRP = (2x + 20) ° and ∠PSQ = 30°, find the value of x.

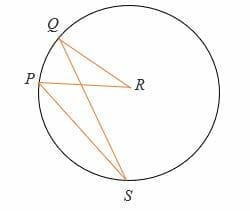
Solution

By inscribed angle theorem,

Central angle = 2 x inscribed angle.

∠QRP =2∠PSQ

∠QRP = 2 x 30°.

= 60°.

Now, solve for x.

⟹ (2x + 20) ° = 60°.

Simplify.

⟹ 2x + 20° = 60°

Subtract 20° on both sides.

⟹ 2x = 40°

Divide both sides by 2.

⟹ x = 20°

So, the value of x is 20°.

Example 3

Solve for angle x in the diagram below.

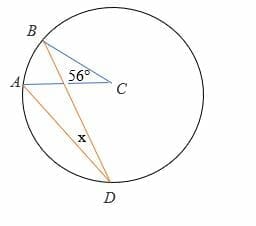
Solution

Given the central angle = 56°

2∠ADB =∠ACB

2x = 56°

Divide both sides by 2.

x = 28°

Example 4

If ∠ YMZ = 150°, find the measure of ∠MZY and ∠ XMY.

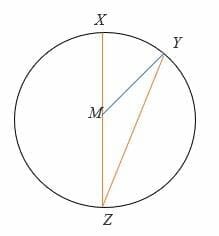
Solution

Triangle MZY is an isosceles triangle, Therefore,

∠MZY =∠ZYM

Sum of interior angles of a triangle = 180°

∠MZY = ∠ZYM = (180° – 150°)/2

= 30° /2 = 15°

Hence, ∠MZY = 15°

And by inscribed angle theorem,

2∠MZY = ∠ XMY

∠ XMY = 2 x 15°

= 30°