Integers – Explanation & Examples
Integers and whole numbers seem to mean the same thing but in real since, the two terms are different. For this reason, many students are perplexed when they encounter problems involving integers and whole numbers.
In this article, we are going to learn about integers and whole numbers. After this discussion you won’t make any more mistakes when using integers and whole numbers.
What is an Integer?
In Mathematics, integers are sets of whole numbers inclusive of positive, negative and zero numbers usually represented by ‘Zahlen’ symbol Z= {…, -4, -3, -2, -1,0,1,2,3, 4…}. It should be noted that an integer can never be a fraction, a decimal or a per cent.
On the other hand, whole numbers are a set of positive and zero numbers without a decimal point or fractions, Whole numbers are represented as W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9……………}.
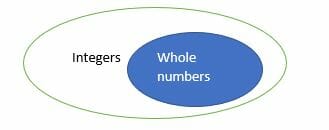
From the above definition of whole numbers and integers, it can be noted that, all whole numbers are integers but not all integers are whole numbers. In short, integers comprise of negative, positive and zero numbers whereas whole numbers comprise of only positive and zero numbers. Therefore, whole numbers are contained in integers.
If you are still doubting, what an integer and a whole number are? Then the flow chart below will give you a more comprehensive understanding.
There are three types integers, namely:
- Positive numbers
- Negative numbers
- The zero
Positive number are whole numbers having a plus sign (+) in front the numerical value. In most cases, the plus sign is ignored simply represented without the symbol. Positive numbers are greater than negative numbers as well a zero. Positive numbers are represented to the right of zero on the number line.
Examples of positive numbers are: 1,2, 88, 800,9900, etc.
Negative numbers are symbolized with a dash or minus sign in front of the numerical value. These numbers are represented on the number line to the left of origin. Examples of negative numbers are: …., – 800, -100, -10, -2, -1.
Zero is a neutral number on the number line. It is neither positive nor negative.
Whole numbers
Whole numbers possess many properties. These properties are based on operations such as adding, subtracting, dividing and multiplying.
For example, the sum of two whole numbers is always a whole. However, subtraction of two whole numbers may result in a whole number of an integer.
Multiplication of two whole numbers results in a whole number. Division on the other may not result in getting a fraction or a whole number.
Now let us see some the properties of whole numbers:
- Closure Property
The closure property of addition and multiplication implies, if x and y are whole numbers, then the product x * y and the sum x + y is also a whole number.
- Commutative Property
If x and y are whole numbers; x + y = y + x and x * y=y * x
- Additive identity
Addition of zero to a whole number leaves the number unchanged; y + 0 = y
- Multiplicative identity
Multiplication of a whole number by 1 leaves the number unchanged; if x is a whole number, then x * 1 = x
- Associative Property
X + (y + z) = (x + y) + z and x * (y z) = (x y) z
- Distributive Property of whole numbers
x * (y + z) = (x y) + (x z) and x * (y-z) = (x y)- (x z)
- Multiplication by zero
If x is a whole number then; x * 0 = 0
- Division of a whole number by zero
If x is a whole number; then x/0 = undefined.
Applications of Integers
Integers and whole numbers are widely applied in different fields. For instance, whole numbers are used to define the population of a given group of quantities. The population can never be negative and hence whole numbers are used.
In banking, integers are used to denote either a debit or a credit.
Integer are also used to describe the temperature of a body either below or above zero centigrade. Integers are also applied in sports to show goal differences.
