Integration by Parts – Definition, Derivation, and Examples

Integration by parts is a helpful technique to learn when integrating complex integrals. This method will open a wide range of complex integrands that we can now work on. When an integrand can be expressed as a product of two simpler functions, the integration by parts (or IBP) may come in handy.

Integration by parts is a special integration technique that allows us to integrate functions that are products of two simpler functions.

In this article, we’ll show you how to apply integration by parts correctly and you’ll learn how to identify integrands that will benefit from this technique. We’ll also show you how the IBP was derived from the product rule of derivatives.

Keep your notes on antiderivative formulas, integral properties, and other integral calculus techniques handy. Review your derivative rules as well since we’ll need them when evaluating indefinite and definite integrals through IBP.

For now, let’s begin by understanding the components that make up the formula for integration by parts.

What is integration by parts?

Integration by parts (IBP) is a helpful technique that allows us to integrate functions that can be written as a product of two functions. It helps us integrate complex functions by rearranging the original function so that we’re left with integrals that are easier to work on. Here are some functions that will be much easier to integrate through the IBP.

\begin{aligned} {\color{Teal} \int x \cos x\phantom{x}dx}, {\color{DarkOrange} \int x^2 \sin x\phantom{x}dx}, {\color{Orchid} \int xe^x\phantom{x}dx}\end{aligned}

When we have an integrand that can be expressed as product of $\boldsymbol{u}$ and $\boldsymbol{dv}$. We can define integration by parts as shown below:

This means that the product of $\boldsymbol{u}$ and $\boldsymbol{dv}$ can be rewritten as the product of the two functions, $\boldsymbol{u}$ and $\boldsymbol{v}$, minus the integral, $\boldsymbol{\int v \phantom{x} du }$. Ideally, $\int v \phantom{x} du$ is a simpler integral.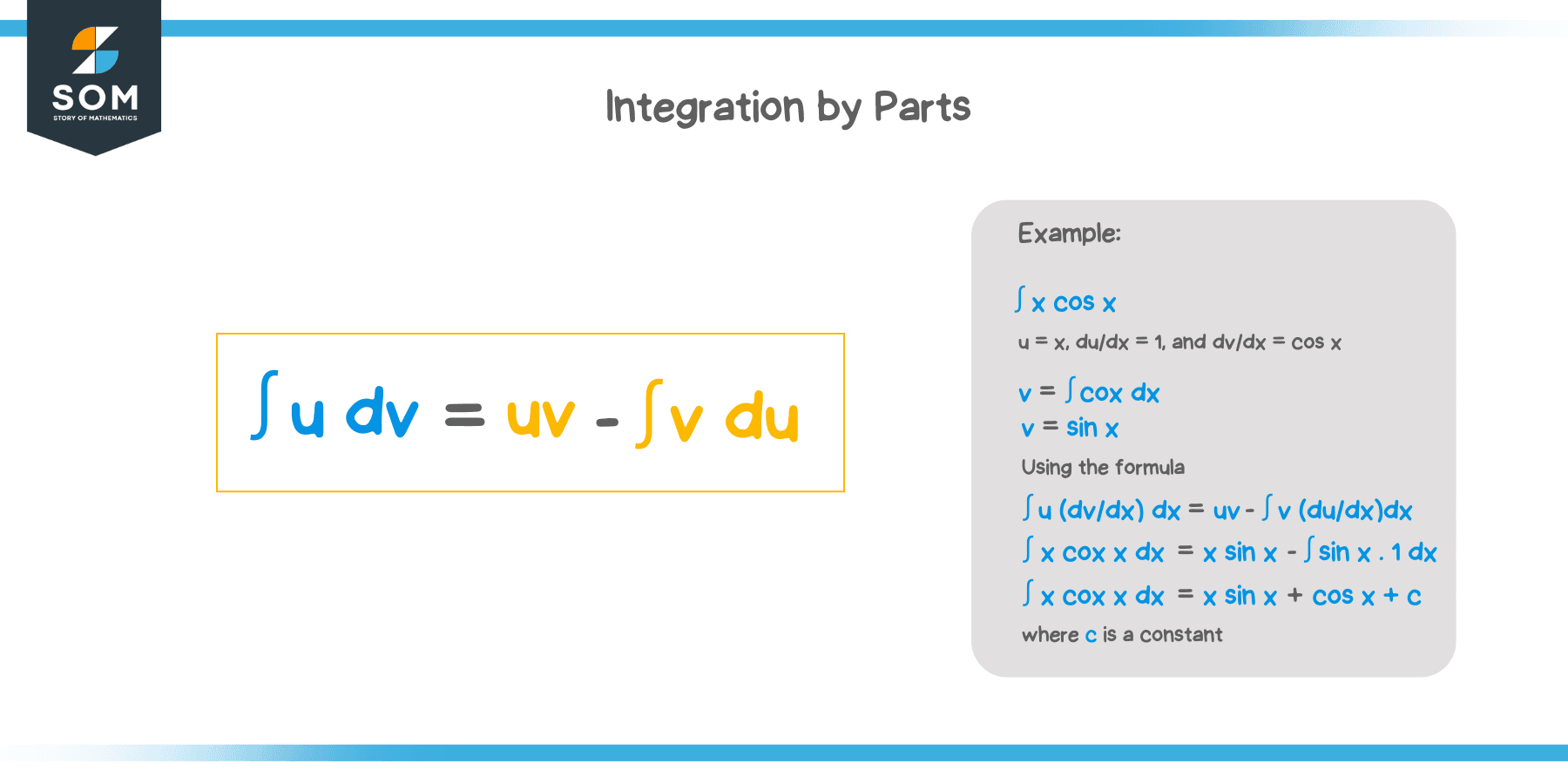

To better understand the formula for integration by parts, we’ve provided proof for the IBP’s formula.

Proof of the integration by parts formula

We’re working with two differentiable functions, $u(x)$ and $v(x)$, so let’s begin with writing $y$ as the product of these two functions.

\begin{aligned}y &= uv\end{aligned}

Apply the product rule for derivatives, $\int fg \phantom{x}dx = \int fg^{\prime} \phantom{x}dx + \int f^{\prime}g \phantom{x}dx$, to rewrite the right-hand side of the equation.

\begin{aligned}\dfrac{d}{dx} y &= \dfrac{d}{dx} (uv)\\\dfrac{dy}{dx} &= u \dfrac{dv}{dx} + v \dfrac{du}{dx} \end{aligned}

Rearrange the terms so that $u \dfrac{dv}{dx}$ is isolated at the left-hand side of the equation.

\begin{aligned}\dfrac{dy}{dx} – v \dfrac{du}{dx} &= u \dfrac{dv}{dx} \\ u \dfrac{dv}{dx}&= \dfrac{dy}{dx} – v \dfrac{du}{dx}\end{aligned}

Integrate both sides of the equation with respect to $x$.

\begin{aligned}\int u \dfrac{dv}{dx} \cdot dx&= \int \left[\dfrac{dy}{dx} – v \dfrac{du}{dx} \right ] \phantom{x}dx\\\int u \phantom{x}dv&= \int \dfrac{dy}{dx} \phantom{x}dx- \int v\dfrac{du}{dx} \phantom{x}dx\\\int u \phantom{x}dv&= \int dy- \int v\phantom{x}du\end{aligned}

Rewrite $\int dy$ as $y$ then substitute it with its original expression, $ y= uv$.

\begin{aligned} \int u \phantom{x}dv&= y- \int v\phantom{x}du\\\int u \phantom{x}dv&= uv- \int v\phantom{x}du\end{aligned} Hence, we’ve shown the general rule for integration by parts. Let’s now break down the steps we’ll be applying when integrating functions by parts.

How to integrate by parts?

Begin by identifying whether the function can be rewritten as a product of two functions. Let’s say we have an integral, $\int f(x)g(x) \phantom{x}dx$, we can apply the following steps to integrate the expression completely.

Step 1: Assign $f(x)$ and $g(x)\phantom{x}dx$ as $u$ and $dv$, respectively.

Step 2: Use the previous step to find $du$ and $v$.

Knowing how to spot which of $f(x)$ and $g(x)$ that is easier to integrate and differentiate is a skill in itself. This is why we’ve included a more thorough discussion in the last section.

Step 3: Use the previous step to find $du$ and $v$ by differentiating $u$ and integrating $dv$.

Step 4: Apply the integration by parts formula, $\int u \cdot dv = uv – \int v \cdot du$, where $\int u \phantom{x}dv = \int f(x)g(x) \phantom{x}dx$.

Step 5: Simplify the right-hand side by evaluating,$\int v(x)\phantom{x}du$.

Let’s apply these steps to integrate the expression, $\int x \cos x \phantom{x}dx$.  Now, it’s time to assign which would best be $u$ and $dv$.

We’ve assigned $x$ as $u$ since it’s easy to differentiate $x$ through the power rule. Similarly, $\cos x \phantom{x}dx$ is a great option for $dv$ since $\int \cos x \phantom{x}dx = \sin x +C$.

Use the expressions from the table to rewrite the integral through IBP.

\begin{aligned}\int {\color{Teal}u }\cdot {\color{DarkOrange}dv} &= {\color{Teal} u}{\color{DarkGreen} v} – \int {\color{DarkGreen} v} \cdot {\color{Orchid} du}\\\int {\color{Teal} x} {\color{DarkOrange} \cos x\phantom{x}dx} &= {\color{Teal} x}{\color{DarkGreen} \sin x} -\int {\color{DarkGreen} \sin x }\cdot {\color{Orchid} 1 \phantom{x}dx}\\&= x\sin x -\int \sin x\phantom{x}dx\end{aligned}

Simplify the expression further by integrating the second term of the right-hand side of the equation.

\begin{aligned}\int x \cos x\phantom{x}dx &= x\sin x – (-\cos x) +C\\&= x\sin x + \cos x + C\end{aligned}

Through integration by parts, we can now evaluate $\int x \cos x\phantom{x}dx$. In fact, we have $\int x \cos x\phantom{x}dx = x\sin x + \cos x + C$.

When evaluating the definite integral, $\int_{a}^{b} f(x)g(x)\phantom{x}dx$, apply the same process but eventually evaluating the result at the two limits: $x =a$ and $x =b$.

\begin{aligned}\int_{a}^{b} u(x) dv &= \left[u(x)v(x)\right]_{a}^{b} – \int_{a}^{b} v(x) du\end{aligned}

When to use integration by parts?

With all the integration techniques we’ve learned at this point, knowing the best time to use the integration by parts is one of the key aspects of acing this technique.

When rewriting the integrand as a product of $f(x)$ and $g(x)$, identify the function that’s easier to differentiate and integrate.

Use the mnemonic, “LIATE”, as a guide in deciding the expression for $u$. Prioritize the following functions in order when selecting which of the two factors are best used as $u$:

When in doubt on the function to assign for $u$, use this mnemonic guide with logarithmic functions as the top choice. Apply other methods to simplify the resulting expression by using integration by parts. 

We’ve prepared more examples for you to master this technique. We’ll also show you additional examples where we use the IBP twice in a row.

Example 1

Evaluate the integral, $\int \dfrac{\ln x}{x^2} \phantom{x}dx$.

Solution

The integrand, $\dfrac{\ln x}{x^2}$, is a product of $\ln x$ and $\dfrac{1}{x^2}$. Through the ILATE mnemonic, a better choice of $u$ is the logarithmic expression, $\ln x$. This makes sense since the derivative of $\ln x$ is $\dfrac{1}{x}$. Hence, we have the following:

Now that we have ${\color{Teal}u }$, ${\color{DarkGreen} v}$, ${\color{DarkOrange}dv}$, and ${\color{Orchid} du}$, apply the formula for the integration by parts technique as shown below.

\begin{aligned}\int {\color{Teal}u }\cdot {\color{DarkOrange}dv} &= {\color{Teal} u}{\color{DarkGreen} v} – \int {\color{DarkGreen} v} \cdot {\color{Orchid} du}\\\int {\color{Teal} \ln x} \cdot {\color{DarkOrange} \dfrac{1}{x^2} \phantom{x}dx} &= {\color{Teal} \ln x}\cdot{\color{DarkGreen} -\dfrac{1}{x}} -\int {\color{DarkGreen} -\dfrac{1}{x} }\cdot {\color{Orchid} \dfrac{1}{x} \phantom{x}dx}\\&= -\dfrac{\ln x}{x}+ \int \dfrac{1}{x^2} \phantom{x}dx\end{aligned}

Simplify the expression by integrating, $\int \dfrac{1}{x^2}\phantom{x}dx$. From the table, we already have, $\int \dfrac{1}{x^2}\phantom{x}dx = -\dfrac{1}{x} + C$.

\begin{aligned}\int \dfrac{\ln x}{x^2} \phantom{x}dx &= -\dfrac{\ln x}{x}+ \left(-\dfrac{1}{x}\right) + C\\&= -\dfrac{\ln x}{x} – \dfrac{1}{x} + C\end{aligned}

Hence, we have $\int \dfrac{\ln x}{x^2} \phantom{x}dx = -\dfrac{\ln x}{x} – \dfrac{1}{x} + C $.

Example 2

Evaluate the integral, $\int (2x – 5)e^x \phantom{x}dx$.

Solution

We can express the integrand as a product of $(2x -5)$ and $e^x$. Both factors are easy to differentiate, but consider the remaining factor that will be integrated as well. Since we know that $\int e^x \phantom{x}dx = e^x + C$, assigning it as $dv$ is a much better option. In addition, when you check the “LIATE” mnemonic, algebraic expressions must be chosen first before exponential functions for $u$.

Let’s go ahead and find $du$ as well as $v$. Here’s a table as a guide so you can double-check your results.

Assign the appropriate expressions for ${\color{Teal}u }$, ${\color{DarkGreen} v}$, ${\color{DarkOrange}dv}$, and ${\color{Orchid} du}$, then use the IBP technique.

\begin{aligned}\int {\color{Teal}u }\cdot {\color{DarkOrange}dv} &= {\color{Teal} u}{\color{DarkGreen} v} – \int {\color{DarkGreen} v} \cdot {\color{Orchid} du}\\\int {\color{Teal} (2x -5)} \cdot {\color{DarkOrange} e^x \phantom{x}dx} &= {\color{Teal} (2x -5)}\cdot{\color{DarkGreen} e^x} -\int {\color{DarkGreen} e^x}\cdot {\color{Orchid} 2\phantom{x}dx}\\&= (2x -5)e^x- \int 2e^x\phantom{x}dx\end{aligned}

Evaluate $\int 2e^x \phantom{x}dx$ using antiderivative formulas to simplify the expression.

\begin{aligned}\int (2x -5)e^x \phantom{x}dx&= (2x -5)e^x- 2\int e^x\phantom{x}dx\\&= (2x -5)e^x – 2e^x + C\\&= (2x -7)e^x + C\end{aligned}

Example 3

Evaluate the integral, $\int x^2 e^x\phantom{x}dx$.

Solution

Similar with the previous example, we assign $u$ to be $x^2$ since it’s the algebraic expression and $dv$ to be $e^x \phantom{x}dx$.

Apply the integration by parts technique and use the expressions we have for  ${\color{Teal}u }$, ${\color{DarkGreen} v}$, ${\color{DarkOrange}dv}$, and ${\color{Orchid} du}$.

\begin{aligned}\int {\color{Teal}u }\cdot {\color{DarkOrange}dv} &= {\color{Teal} u}{\color{DarkGreen} v} – \int {\color{DarkGreen} v} \cdot {\color{Orchid} du}\\\int {\color{Teal} x^2} \cdot {\color{DarkOrange} e^x \phantom{x}dx} &= {\color{Teal} x^2}\cdot{\color{DarkGreen} e^x} -\int {\color{DarkGreen} e^x}\cdot {\color{Orchid} 2x\phantom{x}dx}\\&= x^2e^x- \int 2xe^x\phantom{x}dx\end{aligned}

Let’s now focus on the remaining integral expression, $\int 2xe^x \phantom{x}dx$. We’ll need to apply integration by parts once more to simplify $\int 2xe^x \phantom{x}dx$. This time, we have $u = 2x$ and $dv = e^x \phantom{x}dx$.

\begin{aligned}\int {\color{Teal}u }\cdot {\color{DarkOrange}dv} &= {\color{Teal} u}{\color{DarkGreen} v} – \int {\color{DarkGreen} v} \cdot {\color{Orchid} du}\\\int {\color{Teal} 2x} \cdot {\color{DarkOrange} e^x \phantom{x}dx} &= {\color{Teal} 2x}\cdot{\color{DarkGreen} e^x} -\int {\color{DarkGreen} e^x}\cdot {\color{Orchid} 2\phantom{x}dx}\\&= 2xe^x- \int 2e^x\phantom{x}dx\\&= 2xe^x – 2e^x + C\end{aligned}

From this, we have $\int 2xe^x \phantom{x}dx = 2xe^x – 2e^x + C $. Substitute this expression back into our original expression.

\begin{aligned}\int x^2e^x\phantom{x}dx&= x^2e^x- \int 2xe^x\phantom{x}dx\\&=x^2e^x -(2xe^x – 2e^x ) + C\\&= x^2e^x – 2xe^x + 2e^x  + C\end{aligned}

This example shows that there are instances when we’ll have to apply the IBP twice in a row or even more! As long as we can express the integrand as a product of two simpler functions, IBP can always be an option.

This means that by integrating by parts twice in a row, we have $x^2 e^x\phantom{x}dx x^2e^x – 2xe^x + 2e^x  + C $.

Example 4

Evaluate the integral, $\int_{0}^{\pi} x^2 \cos x\phantom{x}dx$.

Solution

We’ll first focus on integrating the expression completely, so let’s treat the expression as if it’s an indefinite integral first. Since the integrand contains two factors, $x^2$ and $\cos x$, apply integration by parts to evaluate the integral. Begin with $u = x^2$ and $dv = \cos x \phantom{x}dx$.

Use the IBP formula and the expresssions we have for ${\color{Teal}u }$, ${\color{DarkGreen} v}$, ${\color{DarkOrange}dv}$, and ${\color{Orchid} du}$.

\begin{aligned}\int {\color{Teal}u }\cdot {\color{DarkOrange}dv} &= {\color{Teal} u}{\color{DarkGreen} v} – \int {\color{DarkGreen} v} \cdot {\color{Orchid} du}\\\int {\color{Teal} x^2} \cdot {\color{DarkOrange}\cos x \phantom{x}dx} &= {\color{Teal} x^2}\cdot{\color{DarkGreen} \sin x} -\int {\color{DarkGreen} \sin x}\cdot {\color{Orchid} 2x\phantom{x}dx}\\&= x^2\sin x- \int 2x\sin x\phantom{x}dx\end{aligned}

Use integration by parts once more to evaluate $\int 2x\sin x\phantom{x}dx$.

Use these expressions to use the IBP formula once more.

\begin{aligned}\int {\color{Teal}u }\cdot {\color{DarkOrange}dv} &= {\color{Teal} u}{\color{DarkGreen} v} – \int {\color{DarkGreen} v} \cdot {\color{Orchid} du}\\\int {\color{Teal} 2x} \cdot {\color{DarkOrange}\sin x \phantom{x}dx} &= {\color{Teal}2x}\cdot{\color{DarkGreen} -\cos x} -\int {\color{DarkGreen}-\cos x}\cdot {\color{Orchid} 2\phantom{x}dx}\\&=-2x\cos x + \int 2\cos x\phantom{x}dx\\&=-2x\cos x + 2\sin x + C\end{aligned}

We now have $\int 2x \sin x \phantom{x}dx = -2x\cos x + 2\sin x + C$. Going back to our original expression, substitute $\int 2x \sin x \phantom{x}dx$ back into out original integral.

\begin{aligned}\int x^2\cos x\phantom{x}dx&=x^2\sin x-(-2x\cos x+ 2\sin x)+C\\&=x^2 \sin x+ 2x \cos x – 2\sin x + C \end{aligned}

This means that $\int x^2 \cos x\phantom{x}dx = x^2 \sin x- 2x \cos x + 2\sin x + C $. To evaluate $\int_{0}^{\pi} x^2 \cos x\phantom{x}dx$, we simply find the value of  $x^2 \sin x+ 2x \cos x – 2\sin x$ when $x = \pi$ and $x = 0$. Subtract the resulting values to evaluate the definite integral.

\begin{aligned}\int_{0}^{\pi} x^2\cos x\phantom{x}dx &=(x^2\sin x + 2x\cos x – 2\sin x)|_{0}^{\pi}\\&= (\pi^2\sin \pi +2\pi \cos \pi – 2\sin \pi) – (0^2\sin 0 +2(0) \cos 0 – 2\sin 0)\\&=(0 – 2\pi – 0) – (0 + 0 – 0)\\&= -2\pi \end{aligned}

This means that $\int_{0}^{\pi} x^2 \cos x\phantom{x}dx$ is equal to $-2\pi$.

Practice Questions

1. Evaluate the following integrals:
a. $\int \dfrac{\ln x}{x^3} \phantom{x}dx$
b. $\int 4x e^x \phantom{x}dx$
c. $\int 3e^x \sin x \phantom{x}dx$

2. Evaluate the following integrals:
a. $\int (3x – 4)e^x \phantom{x}dx$
b. $\int (5 – 6x)\cos x \phantom{x}dx$
c. $\int (x^2 – 1)\ln x \phantom{x}dx$

3. Evaluate the following integrals:
a. $\int x^2\cos x \phantom{x}dx$
b. $\int (4x^2 – 1) e^x \phantom{x}dx$
c. $\int e^x \sin x \phantom{x}dx$

4. Evaluate the following definite integrals:
a. $\int_{1}^{e} 2x \ln x \phantom{x}dx$
b. $\int_{0}^{\pi} 4x \cos x \phantom{x}dx$
c. $\int_{0}^{4} (2x -1) e^x \phantom{x}dx$
5. Evaluate the following definite integrals:
a. $\int_{1}^{4} x^2e^x\phantom{x}dx$
b. $\int_{0}^{\pi} 2x^2 \sin x \phantom{x}dx$
c. $\int_{0}^{10} (x^2 -1) e^{-x} \phantom{x}dx$

Answer Key

1.
a. $\int \dfrac{\ln x}{x^3} \phantom{x}dx = -\dfrac{\ln x}{2x^2}- \dfrac{1}{4x^2} +C$
b. $\int 4xe^x \phantom{x}dx = 4\left(e^x x – e^x\right) +C $
c. $\int 3e^x \sin x \phantom{x}dx = 3\left(-\dfrac{e^x\cos x}{2} + \dfrac{e^x\sin x}{2}\right) + C $

2.
a. $\int (3x – 4)e^x\phantom{x}dx = (3x -7) e^x + C$
b. $\int (5 -6x)\cos x\phantom{x}dx = (5 – \sin x)\cos x – 6 \cos x + C$
c. $\int (x^2 -1)\ln x\phantom{x}dx = \left(\dfrac{1}{3}x^3 – x\right) \ln x – \dfrac{x^3}{9} + x + C$
3.
a. $\int x^2 \cos x \phantom{x}dx = x^2\sin x – 2\left(-x\cos x + \sin x \right) + C$
b. $\int (4x^2 – 1) e^x\phantom{x}dx = 4e^xx^2 – 8e^xx + 7e^x + C$
c. $\int e^x \sin x\phantom{x}dx = -\dfrac{e^x\cos x}{2} + \dfrac{e^x \sin x}{2} + C$

4.
a. $\int_{1}^{e} 2x \ln x \phantom{x}dx = 2\left(\dfrac{e^2}{4} + \dfrac{1}{4}\right) \approx 4.19$
b. $\int_{0}^{\pi} 4x \cos x \phantom{x}dx = -8$
c. $\int_{0}^{4} (2x -1) e^x \phantom{x}dx = 5e^4 + 3 \approx 275.99$

5.
a. $\int_{1}^{4} x^2e^x\phantom{x}dx = 10e^4 – e \approx 543.26$
b. $\int_{0}^{\pi} 2x^2 \sin x \phantom{x}dx = 2\pi^2 – 4 \approx 11.74$
c. $\int_{0}^{10} (x^2 -1) e^{-x} \phantom{x}dx = -\dfrac{121}{e^{10}} + 1\approx 0.995$