JUMP TO TOPIC
Inverse Matrix – Explanation & Examples
The inverse of a matrix is widely used in linear algebra. It is of immense importance in higher-order linear algebra. For now, we will work on the basics of an inverse of a matrix. Let’s look at the formal definition of an inverse matrix:
The inverse of a matrix $ A $ is $ A^{ – 1 } $, such that multiplying the matrix with its inverse results in the identity matrix, $ I $.
In this lesson, we will take a look at what an inverse matrix is, how to find the inverse of a matrix, the formula for the inverse of a $ 2 \times 2 $ matrix and $ 3 \times 3 $ matrix, and examples to clarify our understanding of matrix inverses.
What is the Inverse of a Matrix?
Remember multiplicative inverses of numbers?
For example, take the number $ 8 $. What number can we multiply $ 8 $ by, to get $ 1 $?
Simple!
It is the reciprocal of $ 8 $, which is $ \frac { 1 }{ 8 } $!
$ 8 \times \frac{1}{8} = 1 $
Similarly, in matrix algebra, matrix inverse plays the same role as a reciprocal in number systems. Inverse matrix is the matrix with which we can multiply another matrix to get the identity matrix (the matrix equivalent of the number $ 1 $)! To know more about the identity matrix, please check here.
Check the picture below:
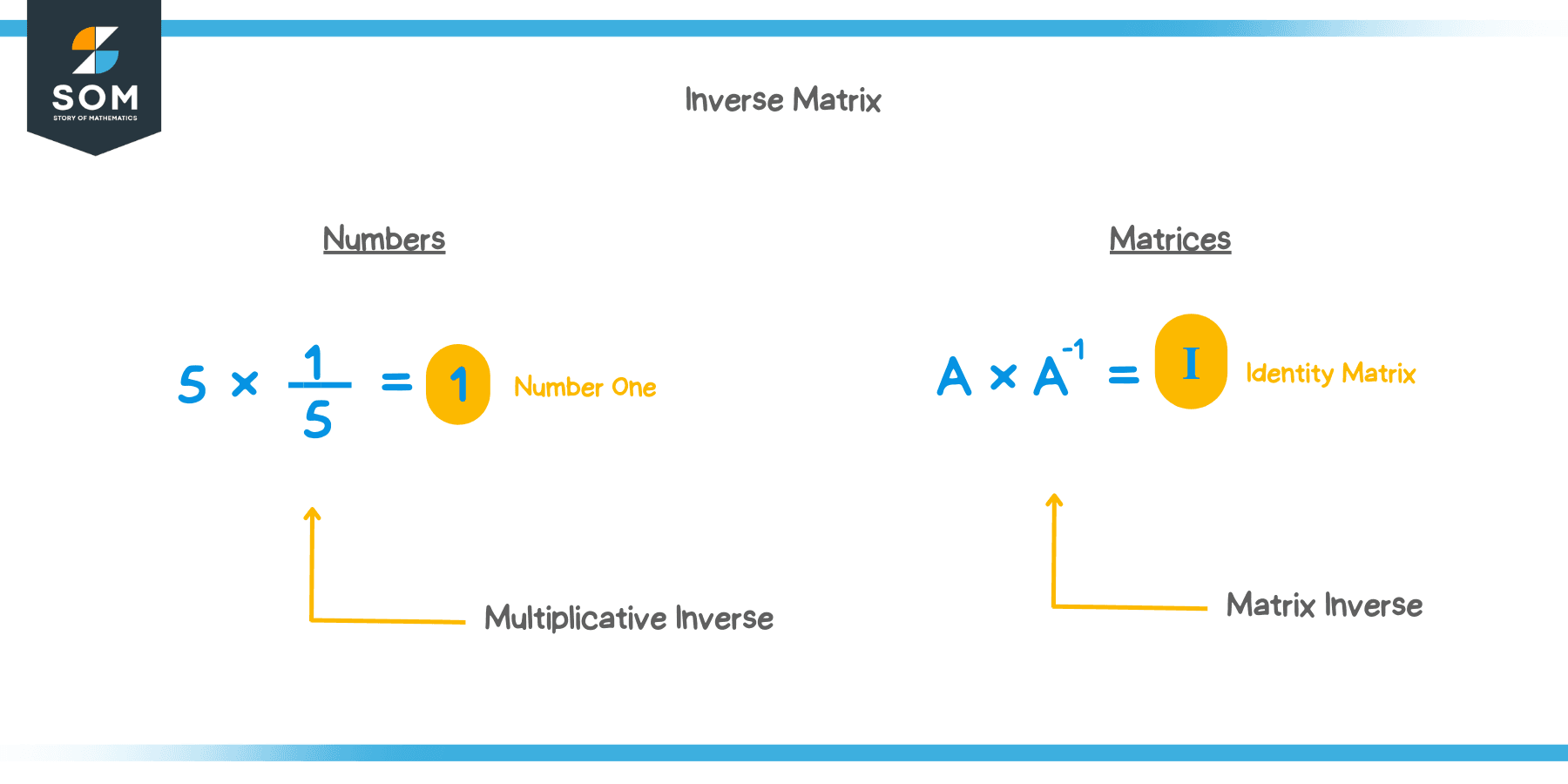
We denote the inverse of Matrix $ A $ as $ A^{ – 1 } $.
The multiplicative inverse (reciprocal) in the number system and the inverse matrix in matrices play the same role. Also, the identity matrix ($ I $ ) (in matrices domain) plays the same role as the number one ( $ 1 $ ).
How to Find the Inverse of a Matrix
So how do we find the inverse of matrices?
To find the inverse of a matrix, we can use a formula that requires a few points to be satisfied before its usage.
Does every matrix have an inverse?
Well, NO!
For a matrix to have an inverse, it has to satisfy $ 2 $ conditions:
- The matrix needs to be a square matrix (the number of rows must be equal to the number of columns).
- The determinant of the matrix (this is a scalar value of a matrix from a few operations done on its elements) must not be $ 0 $.
Remember, not all matrices that are square matrices have an inverse. A matrix whose determinant is $ 0 $ is not invertible (doesn’t have an inverse) and is known as a singular matrix.
Read more about determinants and singular matrices!
We will look at a nifty formula for finding the inverse of a $ 2 \times 2 $ matrix below. Also, the formula for a $ 3 \times 3 $ matrix will be a real messy one! Be prepared! 🙂
Remember,
We can only calculate the inverse for square matrices! Also, the determinant of the matrix cannot be equal to $ 0 $ since the formula requires the division by the determinant. We know division by $ 0 $ is undefined!
Inverse Matrix Formula
We will find the inverse of $ 2 \times 2 $ and $ 3 \times 3 $ matrices in this section.
Inverse of a 2 x 2 Matrix
Consider the $ 2 \times 2 $ matrix shown below:
$ A = \begin{bmatrix} { a } & { b } \\ { c } & { d } \end {bmatrix} $
The formula for the inverse of a $ 2 \times 2 $ matrix (Matrix $ A $ ) is given as:
$ A^{ – 1 } = \frac{ 1 }{ad – bc} \begin{bmatrix} d & { – b } \\ { – c } & a \end {bmatrix} $
The quantity $ ad – bc $ is known as the determinant of the matrix.
Let’s calculate the inverse of a $ 2 \times 2 $ matrix ( Matrix $ B $ ) shown below:
$ B = \begin{bmatrix} 1 & 3 \\ – 3 & 2 \end {bmatrix} $
This is in fact a square matrix and let’s check first if the determinant is $ 0 $ or not. Let’s calculate the determinant:
$ det( B ) = | B | = \begin{vmatrix} 1 & 3 \\ { – 3 } & 2 \end {vmatrix} $
$ = ( 1 ) ( 2 ) – ( 3 ) ( – 3 ) $
$ = 2 + 9 $
$ = 11 $
The determinant isn’t $ 0 $. Now, let’s go ahead and calculate the inverse of matrix $ B $.
$ B^{ – 1 } = \frac{ 1 }{ 11 } \begin{bmatrix} 2 & { – 3 } \\ 3 & 1 \end {bmatrix} $
$ B^{ – 1 } = \begin{bmatrix} {\frac{2}{11}} & { – \frac{3}{11} } \\ { \frac{ 3 }{11}} & { \frac{1}{11} } \end {bmatrix} $
Note: In the last step, we multiplied the scalar constant, $ \frac{1}{11} $, with each element of the matrix. This is the scalar multiplication of a matrix.
Inverse of a 3 x 3 Matrix
Consider the $ 3 \times 3 $ matrix shown below:
$ B = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end {bmatrix} $
The formula for the inverse of a $ 3 \times 3 $ matrix (Matrix $ B $ ) is given as:
$ B^{ – 1 } = \frac{1}{ det(B)} \begin{bmatrix} { (ei – fh) } & { – (bi – ch) } & {(bf – ce)} \\ { – (di- fg) } & { (ai – cg)} & { – (af – cd)} \\ { (dh – eg)} & { – (ah – bg)} & {(ae – bd)} \end {bmatrix} $
Where $ det( B ) $ is the determinant of the $ 3\times3 $ matrix given as:
$ det(B) = a(ei – fh) – b(di – fg) + c(dh – eg) $
Woah! Really messy one!
But nonetheless, let’s calculate the inverse of a $ 3 \times 3 $ matrix ( Matrix $ B $ ) shown below:
$ B = \begin{bmatrix} { 1 } & { 2 } & { – 1 } \\ { 0 } & { 3 } & { – 4 } \\ { – 1 } & { 2 } & { 1 } \end {bmatrix} $
This is in fact a square matrix and let’s check first if the determinant is $ 0 $ or not. Let’s calculate the determinant:
$ det( B ) = | B | = 1 [ ( 3 )( 1 ) – ( – 4 )( 2 ) ] – 2 [ ( 0 )( 1 ) – ( – 4 )( – 1 ) ] + (-1) [ ( 0 )( 2 ) – ( 3 )( – 1 ) ] $
$ = 1 [ 3 + 8 ] – 2 [ 0 – 4 ] + (-1) [ 0 + 3 ] $
$ = 1 [ 11 ] – 2[ – 4 ] – 1[ 3 ] $
$ = 11 + 8 – 3 $
$ = 16 $
The determinant isn’t $ 0 $. Now, let’s go ahead and calculate the inverse of matrix $ B $.
$ B^{ – 1 } = \frac{ 1 }{ det( B ) } \begin{bmatrix} { ( ei – fh ) } & { – ( bi – ch ) } & { ( bf – ce ) } \\ { – ( di – fg ) } & { ( ai – cg ) } & { – ( af – cd ) } \\ { ( dh – eg ) } & { – ( ah – bg ) } & { ( ae – bd ) } \end {bmatrix} $
$ B^{ – 1 } = \frac{ 1 }{ 16 } \begin{bmatrix} { 11 } & { – 4 } & { – 5 } \\ { 4 } & { 0 } & { 4 } \\ { 3 } & { – 4 } & { 3 } \end {bmatrix} $
$ B^{ – 1 } = \begin{bmatrix} { \frac{ 11 }{ 16 } } & { – \frac{1}{4} } & { – \frac{5}{16} } \\ { \frac{ 1 }{ 4 } } & { 0 } & { \frac{1}{4} } \\ { \frac{3 }{16} } & { – \frac{1}{4} } & { \frac{ 3 }{ 16 } } \end {bmatrix} $
Note: In the last step, we multiplied the scalar constant, $ \frac{ 1 }{ 16 } $, with each element of the matrix. This is the scalar multiplication of a matrix.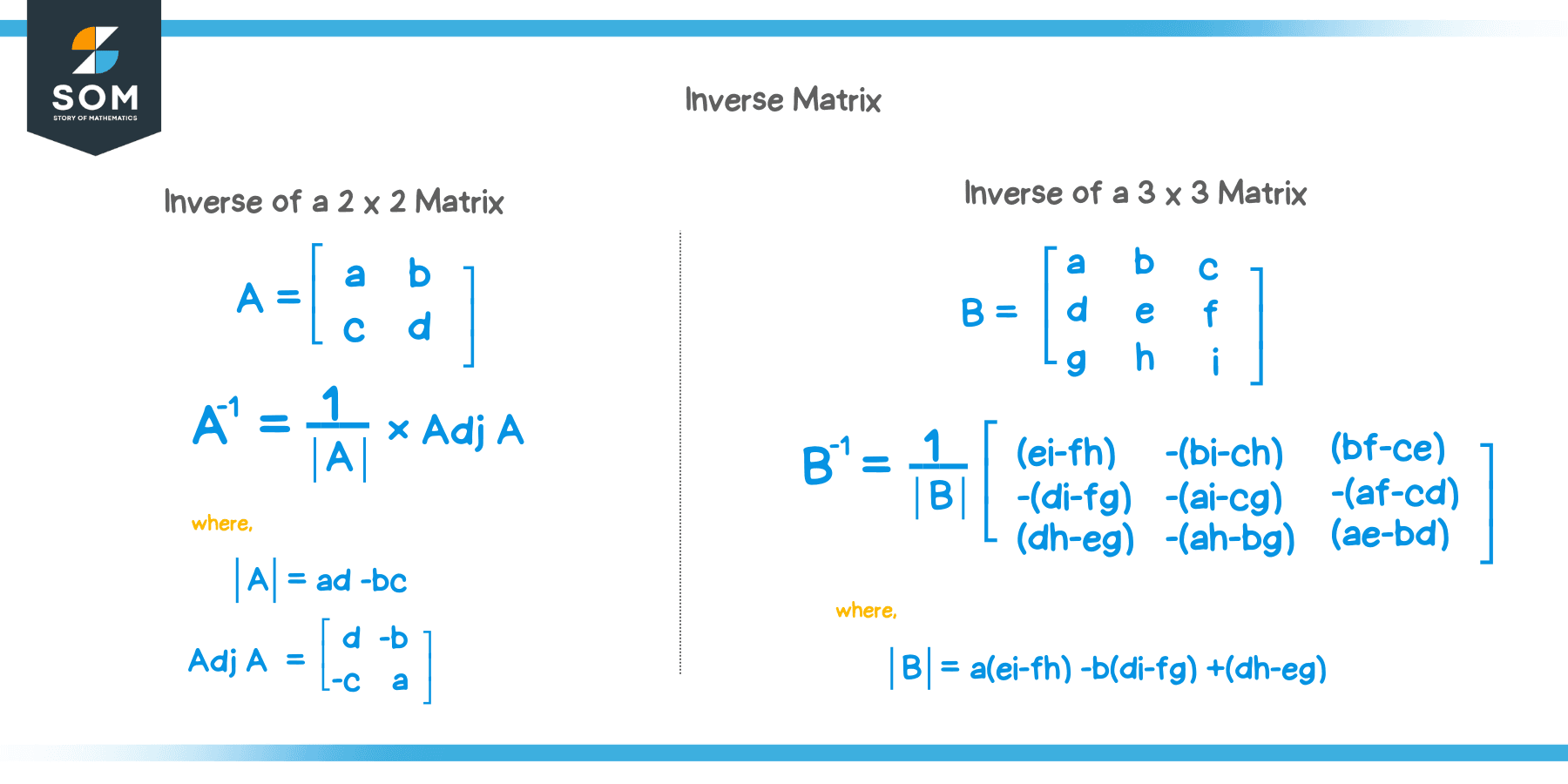
Let’s take a look at a couple of examples!
Example 1
Given $C = \begin{bmatrix} 1 & -2 \\ -3 & -1 \end {bmatrix}$, find $C^{-1}$.
Solution
We will use the formula to find the inverse of Matrix $C$. Shown below:
$ C^{ – 1 } = \frac{ 1 }{ad – bc} \begin{bmatrix} d & { – b } \\ { – c } & a \end {bmatrix} $
$ C^{ – 1 } = \frac{ 1 }{-7} \begin{bmatrix} -1 & 2 \\ 3 & 1 \end {bmatrix} $
$ C^{ – 1 } = \begin{bmatrix} \frac{1}{7} & – \frac{2}{7} \\ -\frac{3}{7} & – \frac{1}{7} \end {bmatrix} $
Example 2
Given $ A= \begin{bmatrix} 0 & -2 \\ -1 & 1 \end {bmatrix} $ and $ B= \begin{bmatrix} -\frac{1}{2} & -1 \\ -\frac{1}{2} & 0 \end {bmatrix}$, confirm if Matrix $B$ is the inverse of Matrix $A$.
Solution
For Matrix $B$ to be the inverse of Matrix $A$, the matrix multiplication between these two matrices should result in an identity matrix. If so, $B$ is the inverse of $A$. Let’s check:
$ A\times B= \begin{bmatrix} 0 & -2 \\ -1 & 1 \end {bmatrix} \times \begin{bmatrix} -\frac{1}{2} & -1 \\ -\frac{1}{2} & 0 \end {bmatrix} $
$ = \begin{bmatrix} (0)(-\frac{1}{2}) + (-2)(-\frac{1}{2}) & (0)(-1) + (-2)(0) \\ (-1)(-\frac{1}{2}) + (1)(-\frac{1}{2}) & (-1)(-1) + (1)(0) \end {bmatrix} $
$ = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end {bmatrix} $
This is the identity matrix.
Thus, Matrix $B$ is the inverse of Matrix $A$.
Practice Questions
Given $A = \begin{bmatrix} 9 & 3 \\ -6 & 9 \end {bmatrix}$, find $A^{-1}$.
Given $B = \begin{bmatrix} 1 & 6 & 4 \\ 2 & 4 & {-1} \\ {-1} & 2 & 5 \end {bmatrix}$, find $B^{-1}$.
Answers
We will use the formula for the inverse of a $ 2 \times 2 $ matrix to find the inverse of Matrix $A$. Shown below:
$ A^{ – 1 } = \frac{ 1 }{ad – bc} \begin{bmatrix} d & { – b } \\ { – c } & a \end {bmatrix} $
$ A^{ – 1 } = \frac{ 1 }{(9)(9) – (3)(-6)} \begin{bmatrix} 9 & -3 \\ 6 & 9 \end {bmatrix} $
$ A^{ – 1 } = \frac{ 1 }{99} \begin{bmatrix} 9 & -3 \\ 6 & 9 \end {bmatrix} $
$ A^{ – 1 } = \begin{bmatrix} \frac{1}{11} & -\frac{1}{33} \\ \frac{2}{33} & \frac{1}{11} \end {bmatrix} $
- This is a $ 3 \times 3 $ square matrix. Let’s calculate the determinant of this matrix.
If we have a $ 3 \times 3 $ matrix $ A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end {bmatrix} $,
the determinant is $ det(A) = a(ei – fh) – b(di – fg) + c(dh – eg) $.
Now, calculating the determinant of our matrix $ B $:
$ det(B) = a(ei – fh) – b(di – fg) + c(dh – eg) $
$ det(B) = 1(20+2) – 6(10-1) + 4(4+4) $
$ det(B) = 1(22) – 6(9) + 4(8) $
$ det(B) = 1(20+2) – 6(10-1) + 4(4+4) $
$det(B) = 0$Since the determinant is $ 0 $, we can’t calculate the inverse of Matrix $B$. Thus, this matrix does not have an inverse!