Inverse trig derivatives – Derivation, Explanation, and Examples
Learning about inverse trig derivatives will pave the way for a better understanding of integrals. Although this topic is very specific towards the inverse trigonometric functions’ derivatives, the resulting algebraic expressions from these inverse trig derivatives will come in handy when we’re integrating functions in our integral calculus classes and discussions.
The derivatives of inverse trigonometric functions are algebraic expressions. These derivatives can be derived by applying the rules for the derivatives of inverse functions.
This article will discuss the six inverse trig derivatives and understand how we can use the derivative rule for inverse functions to derive these rules. Since this is a topic that highlights the properties of inverse trigonometric functions, make sure to refresh your knowledge on the following:
- Refresh how the function and inverse functions are related to each other.
- Recall what the six inverse trigonometric functions are and their important components.
- Review the important trigonometric identities we’ve learned in the past to rewrite trigonometric expressions in different forms.
For now, let’s go ahead and review how we differentiate inverse functions and apply them to find the expressions for the six inverse trig derivatives.
What are the derivatives of inverse trig functions?
First, let’s take a refresher on the six trigonometric functions and their inverse functions. The graphs for each pair of trigonometric and inverse trigonometric functions are shown below as well.
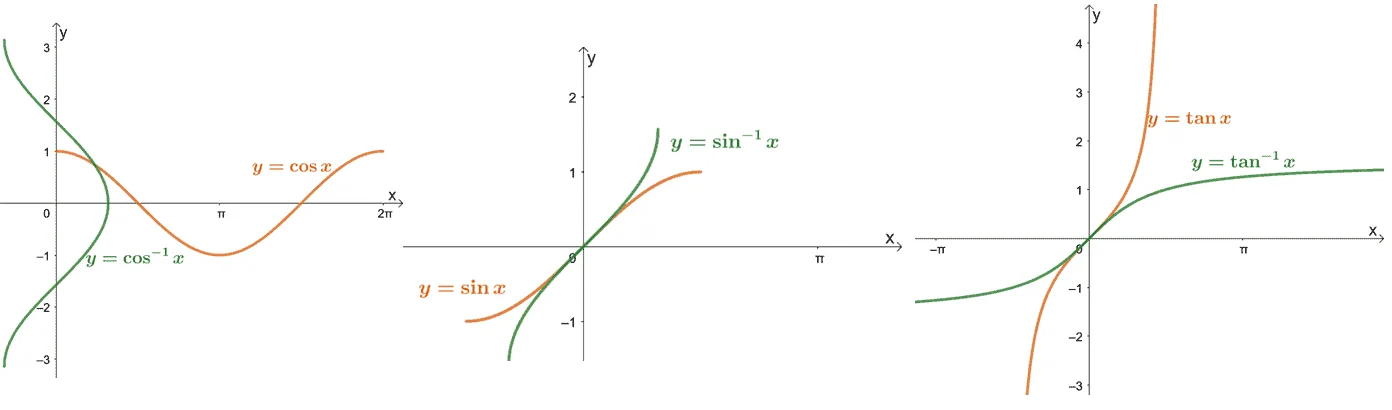
Recall that $\sin^{-1} x$ refers to the actual angle, $\theta$, that returns $x$ when we evaluate $\sin \theta$. The same goes for the rest of the inverse trigonometric functions as shown below.
\begin{aligned} f(x) = \sin x, f^{-1}(x) = \sin^{-1} x \phantom{x}(\text{arcsin})\\ f(x) = \cos x, f^{-1}(x) = \cos^{-1} x \phantom{x}(\text{arccos})\\f(x) = \tan x, f^{-1}(x) = \tan^{-1} x\phantom{x}(\text{arctan})\end{aligned}
We can also determine the derivatives of the inverse functions of these three trigonometric functions’ reciprocals: $\csc x$, $\sec x$, and $\cot x$.
\begin{aligned} f(x) = \csc x, f^{-1}(x) = \csc^{-1} x \phantom{x}(\text{arccsc})\\ f(x) = \sec x, f^{-1}(x) = \sec^{-1} x \phantom{x}(\text{arcsec})\\f(x) = \cot x, f^{-1}(x) = \cot^{-1} x\phantom{x}(\text{arccot})\end{aligned}
For these inverse trigonometric functions to exist, it’ll be important for us to note the domain of each function and make sure we only differentiate throughout the allowed values. These six inverse trigonometric functions will return algebraic expressions for their derivatives, as shown below.
Derivative of Six Inverse Trigonometric Functions | |
\begin{aligned} \dfrac{d}{dx}\sin^{-1}x &= \dfrac{1}{\sqrt{1- x^2}}\\x &\in (-1,1)\end{aligned} | \begin{aligned} \dfrac{d}{dx}\csc^{-1}x &= -\dfrac{1}{|x|\sqrt{x^2 -1}}\\x &\in (-\infty, -1)\cup(1,\infty)\end{aligned} |
\begin{aligned} \dfrac{d}{dx}\cos^{-1}x &= -\dfrac{1}{\sqrt{1- x^2}}\\x &\in (-1,1)\end{aligned} | \begin{aligned} \dfrac{d}{dx}\sec^{-1}x &= \dfrac{1}{|x|\sqrt{x^2 -1}}\\x &\in (-\infty, -1)\cup(1,\infty)\end{aligned} |
\begin{aligned} \dfrac{d}{dx}\tan^{-1}x &= \dfrac{1}{1 + x^2}\\x &\in (-\infty, \infty)\end{aligned} | \begin{aligned} \dfrac{d}{dx}\cot^{-1}x &= -\dfrac{1}{1+x^2}\\x &\in (-\infty, \infty)\end{aligned} |
This is an amazing relationship between functions and their derivatives. That’s because in our previous discussions, we’ve seen how derivatives of algebraic expressions are algebraic expressions themselves and derivatives of trigonometric functions are trigonometric expressions as well. The six inverse trig derivatives are all algebraic expressions – showing how the two groups can be related. This will be extremely helpful when we learn about integrals.
How to derive the inverse trig derivatives?
These six formulas can be derived using the derivative rule for inverse functions. Given that $f(x)$ and $g(x)$ are inverse functions, meaning $g(x) = f^{-1}(x)$, $f[g(x)] =x$ and $g[f(x)] = x$, we can differentiate $g(x)$ as shown below.
\begin{aligned}g'(x) &= \dfrac{1}{f'[g(x)]}\\\dfrac{d}{dx} f^{-1}(x) &= \dfrac{1}{f'[f^{-1}(x)]}\end{aligned}
We can use this rule to derive the derivative rule for $\dfrac{d}{dx} \sin^{-1} x$. We can let $f(x) = \sin x$ and $g(x) = \sin^{-1} x$. For us to find the derivative of $\sin^{-1}{x}$, let’s evaluate $f'[g(x)]$ first. Recall that $\dfrac{d}{dx} \sin x = \cos x$, so $f'[g(x)] = \cos[g(x)] = \cos (\sin^{-1} x)$.
\begin{aligned}g'(x) &= \dfrac{1}{f'[g(x)]}\\\dfrac{d}{dx} \sin^{-1} x &= \dfrac{1}{\cos(\sin^{-1} x)}\end{aligned}
We can use this rule to derive the derivative rule for $\dfrac{d}{dx} \sin^{-1} x$. We can let $f(x) = \sin x$ and $g(x) = \sin^{-1} x$. For us to find the derivative of $\sin^{-1}{x}$, let’s evaluate $f'[g(x)]$ first. Recall that $\dfrac{d}{dx} \sin x = \cos x$, so $f'[g(x)] = \cos[g(x)] = \cos (\sin^{-1} x)$.
The next step will require use to use the Pythagorean identity, $\sin^2 \theta + \cos^2 \theta = 1$, to rewrite $\cos (\sin^{-1} x)$. Keep in mind that for our case, $-\dfrac{\pi}{2}\leq x\leq \dfrac{\pi}{2}$.
\begin{aligned}\sin^2 \theta + \cos^2 \theta &= 1\\\cos \theta &= \sqrt{1-\sin^2\theta}\\\\\cos(\sin^{-1}x) &= \sqrt{1 – [\sin(\sin^{-1}x)]^2}\\&= \sqrt{1 – x^2},\phantom{x}\color{green}\sin(\sin^{-1} x) =x\end{aligned}
Hence, we’ve just proven that $\dfrac{d}{dx} \sin^{-1} x = \dfrac{1}{\sqrt{1 -x^2}}$. We can use a similar approach to confirm the rest of the inverse trigonometric derivatives.
What are examples of functions that require inverse trigonometric derivatives?
We can use the six inverse trigonometric derivative rules whenever we’re given a function or composition of functions that contain inverse trigonometric functions. Here are some examples of functions that may benefit from these inverse trigonometric derivatives:
- $f(x)= \cos^{-1} 4x$
- $g(x) = 5\sin^{-1}(x^2 – 4)$
- $h(x) = -4 + \text{arcsec}(5 – 4x^2)$
We can try differentiating the first example, $f(x) = \cos^{-1} 4x$, to see how we can use apply the derivative rule, $\dfrac{d}{dx} \cos x = – \sqrt{1}{1 – x^2}$. Keep in mind though that we’re working with a composite function, so make sure to apply the chain rule for $f'(x)$.
\begin{aligned}\dfrac{d}{dx} f[g(x)] &= f'[g(x)] \cdot g'(x)\\f(x) &= \cos^{-1} x\\ g(x) &= 4x\\f[g(x)] &= \cos^{-1} (4x)\\\\\dfrac{d}{dx} \cos^{-1} (4x)&= {\color{Purple}-\dfrac{1}{\sqrt{1 – [g(x)]^2}}} \cdot g'(x),\phantom{x} {\color{Purple} \text{Derivative of Cosine Inverse}}\\&= -\dfrac{1}{\sqrt{1 – (4x)^2}} \cdot \dfrac{d}{dx} 4x\\&= -\dfrac{1}{\sqrt{1 – 16x^2}} \cdot {\color{Purple}4\dfrac{d}{dx}x},\phantom{x} {\color{Purple} \text{Constant Multiple Rule}}\\&= -\dfrac{1}{\sqrt{1 – 16x^2}} \cdot {\color{Purple}4(1)},\phantom{x} {\color{Purple} \text{Power Rule}}\\&=-\dfrac{4}{\sqrt{1 – 16x^2}} \end{aligned}
This example also shows how important it is for us to master our fundamental derivative rules and also make sure to apply the chain rule whenever possible. Once you’ve done a quick brush-up, head over to the examples below and try differentiating the given examples using what you’ve just learned in our discussion.
Example 1
Find the derivative of the function, $y =\sin^{-1} \left(\dfrac{2x + 5}{3}\right)$.
Solution
We can see that the function is a composite function with $f(x) = \sin^{-1} x$ as the outer function and $g(x) = \dfrac{2x+5}{3}$ as the inner function. This means that we can use the chain rule and the derivative rule, $\dfrac{d}{dx} \sin^{-1} x = \dfrac{1}{\sqrt{1 -x^2}}$, to find the derivative of $y$.
\begin{aligned}\dfrac{d}{dx} f[g(x)] &= f'[g(x)] \cdot g'(x)\\f(x) &= \sin^{-1} x\\ g(x) &= \dfrac{2x+ 5}{3}\\f[g(x)] &= \sin^{-1} \left(\dfrac{2x + 5}{3} \right )\\\\\dfrac{d}{dx} \sin^{-1} \left(\dfrac{2x + 5}{3} \right )&= {\color{Purple}\dfrac{1}{\sqrt{1 – [g(x)]^2}}} \cdot g'(x),\phantom{x} {\color{Purple} \text{Derivative of Sine Inverse}}\\&= \dfrac{1}{\sqrt{1 – \left(\dfrac{2x + 5}{3}\right)^2}} \cdot \dfrac{d}{dx} \dfrac{2x+5}{3}\\&= \dfrac{1}{\sqrt{1 – \left(\dfrac{2x + 5}{3}\right)^2}} \cdot {\color{Purple}\dfrac{2}{3}\dfrac{d}{dx} \left(x + \dfrac{5}{2}\right)},\phantom{x} {\color{Purple} \text{Constant Multiple Rule}}\\&= \dfrac{1}{\sqrt{1 – \left(\dfrac{2x + 5}{3}\right)^2}} \cdot \dfrac{2}{3}({\color{Purple} 1} + {{\color{Teal} 0}}),\phantom{x} {\color{Purple} \text{Power Rule }} \text{&}{\color{Teal} \text{ Constant Rule}}\end{aligned}
We can simplify the expression further by factoring out $\dfrac{1}{3}$ from the rational expression inside the square root. We can then expand the expression inside the radical using the algebraic property, $(a + b)^2 = a^2 + 2ab +b^2$.
\begin{aligned}y’ &= \dfrac{1}{\sqrt{1 – \left(\dfrac{2x + 5}{3}\right)^2}} \cdot \dfrac{2}{3}(1)\\&= \dfrac{1}{\sqrt{1 – \left( \dfrac{1}{3}\right )^2(2x +5)^2}} \cdot \dfrac{2}{3}\\&= \dfrac{2}{3\sqrt{1 – \dfrac{1}{9}(4x^2 + 20x + 25)}}\\&= \dfrac{2}{3\sqrt{\dfrac{9-4x^2 – 20x – 25}{9}}}\\&= \dfrac{2}{3\sqrt{1 – \dfrac{1}{9}(4x^2 + 20x + 25)}}\\&= \dfrac{2}{3\sqrt{\dfrac{4}{9}(-x^2 -5x-4)}}\\&= \dfrac{2}{3\cdot \dfrac{2}{3}\sqrt{-x^2 -5x-4}}\\&= \dfrac{1}{-x^2 -5x -4}\end{aligned}
After a few more algebraic manipulations, we have the simplified form of $y’$. Hence, we have $y’ = \dfrac{1}{-x^2 -5x -4}$.
Example 2
Find the derivative of the function, $y = \csc^{-1} (2x^2 – 3)$.
Solution
This time, we’re working with a function that contains the inverse of cosecant. Recall that $\dfrac{d}{dx} \csc x = -\dfrac{1}{|x|\sqrt{x^2 -1}}$, so we can use this differentiate $y$. Since we have $2x^2 – 3$ inside the function of $\csc^{-1} x$, make sure to apply the chain rule as well.
\begin{aligned}\dfrac{d}{dx} f[g(x)] &= f'[g(x)] \cdot g'(x)\\f(x) &= \sin^{-1} x\\ g(x) &= 2x^2 -3\\f[g(x)] &= \csc^{-1} (2x^2 -3)\\\\\dfrac{d}{dx} \csc^{-1} (2x^2 -3)&= {\color{Purple}-\dfrac{1}{|g(x)|\sqrt{[g(x)]^2 -1}}} \cdot g'(x),\phantom{x} {\color{Purple} \text{Derivative of Cosecant Inverse}}\\&= -\dfrac{1}{|2x^2 -3|\sqrt{(2x^2 – 3)^2 – 1}} \cdot \dfrac{d}{dx} (2x^2 -3)\\&= -\dfrac{1}{|2x^2 -3|\sqrt{(2x^2 – 3)^2 – 1}} \cdot {\color{Purple}\left( \dfrac{d}{dx} 2x^2 -\dfrac{d}{dx} 3\right )},\phantom{x} {\color{Purple} \text{Sum Rule}}\\&= -\dfrac{1}{|2x^2 -3|\sqrt{(2x^2 – 3)^2 – 1}} \cdot \left( {\color{Purple}2\dfrac{d}{dx} x^2} – {\color{Teal} 0}\right ),\phantom{x}{\color{Purple} \text{Constant Multiple Rule }} \text{&} {\color{Teal} \text{ Constant Rule}}\\&= -\dfrac{1}{|2x^2 -3|\sqrt{(2x^2 – 3)^2 – 1}} \cdot {\color{Purple}\left(4x\right )},\phantom{x} {\color{Purple} \text{Power Rule}} \end{aligned}
We can continue to simplify $y’$ by expanding $(2x^2 – 3)^2$ and eventually factoring out $\sqrt{4}$ to simplify the resulting rational expression.
\begin{aligned}y’&= -\dfrac{4x}{|2x^2 -3|\sqrt{(2x^2 – 3)^2 – 1}} \\&= -\dfrac{4x}{|2x^2 -3|\sqrt{4x^4 – 12x^2 + 9 – 1}}\\&= -\dfrac{4x}{|2x^2 -3|\sqrt{4(x^4 – 3x^2 + 2)}}\\&= -\dfrac{4x}{|2x^2 -3|\sqrt{4x^4 – 12x^2 + 9 – 1}}\\&= -\dfrac{4x}{|2x^2 -3|\sqrt{4}\sqrt{(x^4 – 3x^2 + 2)}} \\&= -\dfrac{2x}{|2x^2 -3|\sqrt{4x^4 – 12x^2 + 9 – 1}}\\&= -\dfrac{2x}{|2x^2 -3|\sqrt{(x^4 – 3x^2 + 2)}} \end{aligned}
This shows that $y’ = -\dfrac{2x}{|2x^2 -3|\sqrt{(x^4 – 3x^2 + 2)}}$.
Example 3
Find the derivative of the function, $y = \tan^{-1} \left(\dfrac{e^x}{2x – 1}\right)$.
Solution
The function is once again a composite function with $f(x) = \tan^{-1} x$ as the outer function and $g(x) = \dfrac{e^x}{2x -1}$ as the inner function. What we can do is use the inverse trigonometric derivative, $\dfrac{d}{dx} \tan x = \dfrac{1}{1 + x^2}$, and of course, apply the chain rule. We can then use fundamental derivative rules to further simplify $y’$.
\begin{aligned}\dfrac{d}{dx} f[g(x)] &= f'[g(x)] \cdot g'(x)\\f(x) &= \tan^{-1} x\\ g(x) &= \dfrac{e^x}{2x – 1}\\f[g(x)] &= \tan^{-1} \left(\dfrac{e^x}{2x – 1} \right )\\\\\dfrac{d}{dx} \tan^{-1} \left(\dfrac{e^x}{2x – 1} \right )&= {\color{Purple}\dfrac{1}{1 + [g(x)]^2}} \cdot g'(x),\phantom{x} {\color{Purple} \text{Derivative of Tangent Inverse}}\\&= \dfrac{1}{1 + \left(\dfrac{e^x}{2x – 1} \right )^2} \cdot \dfrac{d}{dx} \left(\dfrac{e^x}{2x – 1} \right ) \end{aligned}
We can use the quotient rule to differentiate $\dfrac{e^x}{2x – 1}$ as shown below.
\begin{aligned}\dfrac{d}{dx}\dfrac{e^x}{2x – 1} &= \dfrac{(2x -1)\dfrac{d}{dx}e^x – e^x \dfrac{d}{dx} (2x- 1)}{(2x – 1)^2}\\&= \dfrac{{\color{Purple}e^x}(2x -1) -e^x \dfrac{d}{dx} (2x- 1)}{(2x – 1)^2},\phantom{x}\color{Purple} \dfrac{d}{dx} e^x = e^x\\&= \dfrac{e^x(2x -1) -e^x\color{Purple} \left(\dfrac{d}{dx}2x – \dfrac{d}{dx}1 \right )}{(2x – 1)^2},\phantom{x}\color{Purple} \text{Sum Rule}\\&= \dfrac{e^x(2x -1) -e^x \left({\color{Purple}2\dfrac{d}{dx}x} – {\color{Orange} 0} \right )}{(2x – 1)^2},\phantom{x}{\color{Purple} \text{Constant Multiple Rule }} \text{&} {\color{Orange} \text{ Constant Rule }}\\&= \dfrac{e^x(2x -1) -(e^x)(2)\color{Purple} \left(1\right )}{(2x – 1)^2},\phantom{x}\color{Purple} \text{Power Rule}\\&= \dfrac{e^x(2x -3)}{(2x- 1)^2}\end{aligned}
We can replace $\dfrac{e^x}{2x – 1}$ with $\dfrac{e^x(2x -3)}{(2x- 1)^2}$ into our expression for $y’$. Simplify the expression for $y’$ using your algebraic techniques.
\begin{aligned}y’&= \dfrac{1}{1 + \left(\dfrac{e^x}{2x – 1} \right )^2} \cdot {\color{Purple}\dfrac{e^x(2x -3)}{(2x- 1)^2}},\phantom{x} \color{Purple}\text{Quotient Rule}\\&= \dfrac{e^x(2x -3)}{1 \cdot (2x – 1)^2 +\left(\dfrac{e^x}{2x – 1} \right )^2 \cdot (2x – 1)^2 }\\&= \dfrac{e^x(2x – 3)}{(2x -1)^2 + e^{2x}}\end{aligned}
This means that $y’ = \dfrac{e^x(2x – 3)}{(2x -1)^2 + e^{2x}}$ or if we distribute $e^x$ in the numerator, we have $y’ = \dfrac{2e^xx – 3e^x}{(2x -1)^2 + e^{2x}}$.
Practice Questions
1. Find the derivative of the functions shown below.
a. $f(x) = \sin^{-1} (4x – 5)$
b. $g(x)=\cos^{-1} \left(\dfrac{x^2 + 6}{4}\right)$
c.$h(x) = \text{arctan } (\sqrt{2x + 5})$
2. Find the derivative of the functions shown below.
a. $f(x) = \csc^{-1} (6x – 5)$
b. $g(x) = \sec^{-1} (3x – 1)$
c.$h(x) = \text{arccot } \left(\dfrac{2}{x} – 1\right)$
3. Find the derivative of the functions shown below.
a. $f(x) = \cot^{-1} \dfrac{e^x}{3x – 5}$
b. $g(x) = \tan^{-1} \sqrt{4x^2 – 8}$
c.$h(x) = \text{arcsin } e^x(4x -1)$
Answer Key
1.
a. $f'(x) = \dfrac{4}{\sqrt{-16x^2 +40x -24}}$
b. $g'(x) = -\dfrac{2x}{\sqrt{-x^4 – 12x^2 -20}}$
c. $h'(x) = \dfrac{1}{(2x + 6)\sqrt{2x +5}}$
2.
a. $f'(x) = -\dfrac{6}{|6x – 5|\sqrt{36x^2 -60x +24}}$
b. $g'(x) = \dfrac{3}{|3x – 1|\sqrt{9x^2 – 6x}}$
c. $h'(x) = \dfrac{1}{x^2 – 2x + 2}$
3.
a.$f'(x) = -\dfrac{3e^xx-8e^x}{e^{2x}+\left(3x-5\right)^2}$
b. $g'(x) = \dfrac{2x}{(4x^2 -7)(\sqrt{x^2 – 2})}$
c. $h'(x) = \dfrac{4e^xx+3e^x}{\sqrt{1-e^{2x}\left(4x-1\right)^2}}$
Images/mathematical drawings are created with GeoGebra.