The Cosine Rule – Explanation & Examples

In the last article, we saw how the sine rule helps us calculate the missing angle or missing side when two sides and one angle is known or when two angles and one side are known.

But what will you do when you are only given the three sides of a triangle, and you need to find all the angles?

In the 15^th century, that issue was resolved when a Persian mathematician, Jamshid al-Kashi, presented the Law of Cosines in a form suitable for triangulation. In France, it is still known as a Theoreme d’Al-Kashi.

In this article, you will learn about:

• The law of cosines,
• how to apply the law of cosines to solve problems and,
• the law of cosines formula.

What is the Law of Cosines?

The law of cosines also referred to as the cosine rule, is a formula that relates the three side lengths of a triangle to the cosine.

The cosine rule is useful in two ways:

• We can use the cosine rule to find the three unknown angles of a triangle if the three side lengths of the given triangle are known.
• We can also use the cosine rule to find the third side length of a triangle if two side lengths and the angle between them are known.

The law of cosines formula

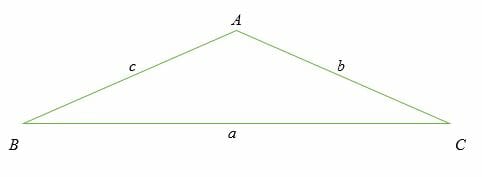
Consider an oblique triangle ABC shown below. An oblique triangle is a non-right triangle. Remember that the side lengths are labeled in lower case letters, while the angles are labeled in capital letters.

Also, note that for each angle, the opposite side length is labeled using the same letter.

The law of cosines states that:

⇒ (a) ² = [b² + c² – 2bc] cos (A)

⇒ (b) ² = [a² + c² – 2ac] cos (B)

⇒ (c) ² = [a² + b² – 2bc] cos (C)

You noticed that the equation c² = a² + b² – 2bc cos (C) resembles the Pythagorean Theorem, except for the last terms,” – 2bc cos (C).” For this reason, we can say that the Pythagorean Theorem is a special of the sine rule.

Proof of the law of cosines

The cosine rule can be proved by considering the case of a right triangle. In this case, let’s drop a perpendicular line from point A to point O on the side BC.

Let side AM be h.

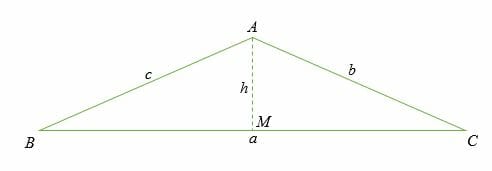
In the right triangle ABM, the cosine of angle B is given by:

Cos (B) = Adjacent/Hypotenuse = BM/BA

Cos (B) = BM/c

BM = c cos (B)

Given that BC = a, therefore, MC is calculated as;

MC = a – BM

 = a – c cos (B) ……………………………………………… (i)

In triangle ABM, the sine of angle B is given by;

Sine B = Opposite/Hypotenuse = h/c

h = c sine B …………………………………………………… (ii)

By applying the Pythagorean theorem in right triangle AMC, we have,

AC² = AM² + MC²……………………………………………… (iii)

Substitute equation (i) and (ii) in equation (iii).

b² = (c Sine B)² + (a – c Cos B)²

b² = c² Sine ² B + a² – 2ac Cos B + c² Cos ² C

Rearranging the above equation:

b² = c² Sine ² B + c² Cos ² C + a² – 2ac Cos B

Factoring.

b² = c² (Sine ² B + Cos ² C) + a² – 2ac Cos B

But, from trigonometric identities, we know that,

sin²θ + cos²θ = 1

Therefore, b² = c² + a² – 2ac Cos B

Hence, the cosine law is proved.

How to Use the Cosine Rule?

If you we need to find the side lengths of a triangle, we use the cosine rule in the form of;

⇒ (a) ² = [b² + c²– 2bc] cos (A)

⇒ (b) ² = [a² + c² – 2ac] cos (B)

⇒ (c) ² = [a² + b² – 2bc] cos (C)

And if we need to find the size of an angle, we use the cosine rule of the form;

⇒ cos A = (b² + c² – a²)/2bc

⇒ cos B = (a² + c²– b²)/2ac

⇒ cos C = (a² + b²– c²)/2ab

Let’s now check our understanding of the cosine rule by attempting a few sample problems.

Example 1

Calculate the length of side AC of the triangle shown below.

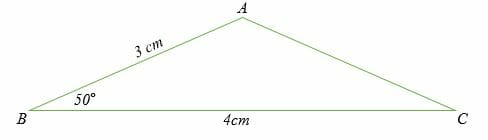
Solution

Because we want to calculate the length, we will therefore use the

cosine rule in the form of;

⇒ (b) ² = [a² + c² – 2ac] cos (B)

By substitution, we have,

b² = 4² + 3² – 2 x 3 x 4 cos (50)

b² = 16 + 9 – 24cos50

= 25 – 24cos 50

b² = 9.575

Determine the square root of both sides to get,

b = √9.575 = 3.094.

Therefore, the length of AC = 3.094 cm.

Example 2

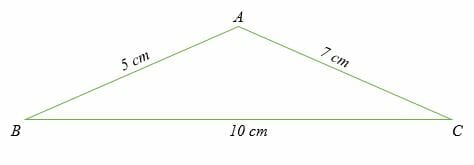
Calculate all three angles of the triangle shown below.

Solution

Since all the three side lengths of the triangle are given, then we need to find the measures of the three angles A, B, and C. Here, we will use the cosine rule in the form;

⇒ Cos (A) = [b² + c² – a²]/2bc

⇒ Cos (B) = [a² + c²– b²]/2ac

⇒ Cos (C) = [a² + b²– c²]/2ab

Solve for angle A:

Cos A = (7² + 5² – 10²)/2 x 7 x 5

Cos A = (49 + 25 – 100)/70

Cos A = -26/70

Cos A = – 0.3714.

Now, determine the cos inverse of – 0.3714.

A = Cos ^-1 – 0.3714.

A = 111.8°

Solve for angle B:

By substitution,

cos B = (10² + 5²– 7²)/2 x 10 x 7

Simplify.

Cos B = (100 + 25 – 49)/140

Cos B = 76/140

Determine the cos inverse of 76/140

B = 57.12°

Solve for angle C:

By substitution,

cos C = (10² + 7²– 5²)/2 x 10 x 7

Cos C = (100 + 49 – 25)/140

Cos C = 124/140

Determine the cos inverse of 124/140.

C = 27.7°

Hence, the three angles of the triangle are; A = 111.8°, B = 57.12°, and C = 27.7°.