
The aim of this question is to analyze the bell curve. The given curve is a perfect bell shape because, from the mean, the values are the same on both sides, i.e., on the left and right. This question is related to the concepts of mathematics.
Here, we have to calculate three basic parameters: mean μ, one standard deviation away from the mean μ+σ, and standard deviation σ.
Expert Answer
For finding mean ($\mu$): We know that the normal curve shows the normal distribution, and in the above curve, we have three standard deviations, i.e., one, two, and three standard deviations on both sides of the mean.
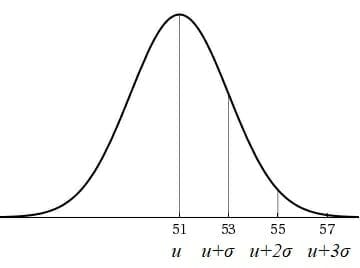
Figure 1
From the curve, the parameter which is at the center can be identified as the mean $\mu$. Therefore:
\[ \mu = 51 \]
One standard deviation away from the mean: We have identified the three standard deviations as $(\mu + \sigma)$, $(\mu + 2\sigma)$, and $(\mu + 3\sigma)$, with their values. Therefore, the required one standard deviation away from the mean is calculated as follows:
\[ \mu + \sigma = 53 \]
For the calculation of standard deviation: The standard deviation is the value away from the mean. It can be calculated as follows:
We have
\[ \mu + \sigma = 53 \]
\[ 51 + \sigma = 53 \]
\[ \sigma = 2 \]
Numerical Results
The required numerical results are as follows.
For finding mean ($\mu$):
\[ \mu = 51 \]
One standard deviation away from mean:
\[ \mu + \sigma = 53 \]
The calculation of standard deviation:
\[ \sigma = 2 \]
Example
The mean $\mu$ of a bell curve is $24$ and its variance $\sigma$ is $3.4$. Find standard deviations up to $3\sigma$.
The given values are:
\[ \mu = 24 \]
\[ \sigma = 3.4 \]
The standard deviations are given as:
The $1st$ standard deviation is given as:
\[ \mu + 1\sigma = 24 + 3.4 \]
\[ \mu + 1\sigma = 27.4 \]
The $2nd$ standard deviation is given as:
\[ \mu + 2\sigma = 24 + 2 \times 3.4 \]
\[ \mu + 2\sigma = 24 + 6.8 \]
\[ \mu + 2\sigma = 30.8 \]
The $3rd$ standard deviation is given as:
\[ \mu + 3\sigma = 24 + 3 \times 3.4 \]
\[ \mu + 3\sigma = 24 + 10.2 \]
\[ \mu + 3\sigma = 34.2 \]
Images/ Mathematical drawings are created with Geogebra.
