JUMP TO TOPIC
Midpoint Formula – Explanation and Examples
The midpoint formula is a method for finding the exact center of a line segment.
Since a line segment, by definition, is finite, it has two end points. Therefore, another way to think about the midpoint formula is to think of it as a way to find the point exactly between two other points.
The midpoint formula requires us to plot points and a thorough knowledge of fractions.
In this section, we will go over:
- What is the Midpoint Formula?
- How to Find the Midpoint of a Line
What is the Midpoint Formula?
Given two points (x1, y1) and (x2, y2), the midpoint formula is ((x1+x2)/2, (y1+y2)/2).
If we are trying to find the center of a line segment, the points (x1, y1) and (x2, y2) are the end points of the line segment.
Notice that the output of the midpoint formula is not a number. It is a set of coordinates, (x, y). That is, the midpoint formula gives us the coordinates for a point that is exactly between the two given points. This is the exact middle of a line segment connecting the two points.
The distance from either point to the midpoint will be exactly half the distance between the two initial points.
How to Find the Midpoint of a Line
First, pick a point to be (x1, y1) and a point to be (x2, y2). It doesn’t matter much which is which, but in some cases, we may have to determine the coordinates of the two points from a graph.
Then, we can plug the values x1, y1, x2, and y2 into the formula ((x1+x2)/2, (y1+y2)/2).
Remember learning about averages and means? To find the average or mean of two numbers, we add the two numbers together and divide by two. That’s exactly what we are doing in the formula!
Therefore, we can think of the midpoint formula as finding the point that is the average of the x-terms and the y-terms.
Examples
In this section, we will go over some examples of how to use the midpoint formula and their step-by-step solutions.
Example 1
Consider a line segment that starts at the origin and ends at the point (0, 4). What is the midpoint of this line?
Example 1 Solution
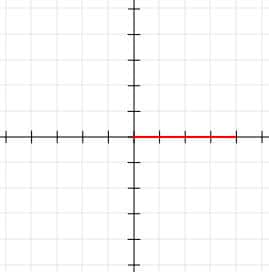
It is easy to see that this line is 4 units in length and its midpoint is (2, 0). This makes it easy to illustrate how the midpoint formula works.
First, let’s designate the origin, (0, 0) as (x1, y1) and the point (4, 0) as (x2, y2). Then we can plug them into the midpoint formula:
((x1+x2)/2, (y1+y2)/2).
((4+0)/2, (0+0)/2).
(4/2, 0)
(2, 0).
This matches with our intuition. After all, the midpoint of 0 and 4 is 2.
Example 2
Consider a line segment that starts at (0, 2) and ends at (0, 4). What is the midpoint of this line segment?
Example 2 Solution
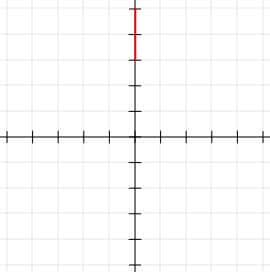
Again, we can see that this is a line segment of length 2 units. Its midpoint is one unit from each end point at (0, 3). This once again makes it easy to demonstrate how the midpoint formula works.
Let’s let (0, 2) be (x1, y1) and (0, 4) be (x2, y2). Then, plugging the values into the midpoint formula gives us:
((0+0)/2, (4+2)/2)
(0, 6/2)
(0, 3).
Therefore, the midpoint is (0, 3), and, as before, this matches our intuition.
Example 3
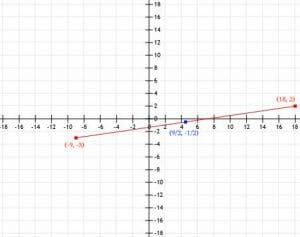
Find the midpoint of a line segment that extends from (-9, -3) to (18, 2).
Example 3 Solution
It is not as immediately obvious where the midpoint of this line is. But, we can still assign one point (let’s say (-9, -3) as (x1, y1)) and the other point as (x2, y2). Then, we can insert the values into the midnight formula:
((-9+18)/2, (-3+2)/2)
(9/2, -1/2).
In this case, we can just leave the two numbers as fractions for our answer. All three points are plotted below.
Example 4
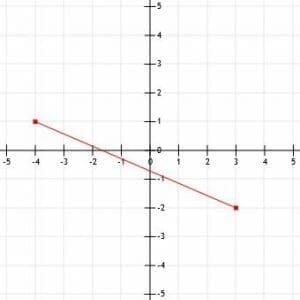
The graph below features a line segment k. What is the midpoint of the line segment?
Example 4 Solution
Before we can determine the midpoint of this line segment, we need to find the coordinates of its endpoints. The endpoint in the second quadrant is four units left of the origin and one unit above it. The endpoint in the fourth quadrant is three units to the right of the origin and three units below it. This means that the endpoints are (-4, 1) and (3, -3) respectively. Let’s also have them be (x1, y1) and (x2, y2) respectively.
When we insert these values into the midpoint formula, we get:
((-4+3)/2, (3+1)/2)
(-1/2, -2/2)
(-1/2, -1).
Therefore, the exact center of this line segment is the point (-1/2, -1).
Example 5
A scientist finds two nests for an endangered bird on an island. One nest is 1.2 miles north and 1.4 miles east of the scientist’s research facility. The second nest is 2.1 miles south and 0.4 miles east of the facility. The scientist wants to set up one camera in a spot that is as close as possible to both nests in hopes of catching some footage of the birds. Where should she put this camera?
Example 5 Solution
The spot that will minimize the distance to each nest is the midpoint between the coordinates of the two nests.
Let’s let north and east be the positive directions. Since the first nest is 1.2 miles north and 1.4 miles east, we can plot its coordinates at (1.4, 1.2). Similarly, the coordinates of the second nest are at (0.4, -2.1).
If the coordinates of the first nest are (x1, y1) and the coordinates of the second nest are (x2, y2), then the midpoint is:
((1.4+0.4)/2, (1.2-2.1)/2)
(1.8/2, -0.9/2)
(0.9, -0.9/2)
That is, the scientist should set up her camera at the coordinates (0.9, -0.9/2). Since -0.9/2 is -0.45, the camera should be at a spot 0.45 miles north of the facility and 0.9 miles east of it.
Example 6
The midpoint of a line segment is (9, 4). One of the endpoints of the line segment is (-8, -2). What is the other endpoint of this line segment?
Example 6 Solution
We can plug the values we know into the midpoint formula and work backwards. We know that the midpoint is (9, 4) and that one end point is (-8, -2). Let’s let this be (x1, y1). Then, we have:
(-8+x2)/2=9 and (-2+y2)/2=4.
Now, we can multiply both sides of both equations by 2, which gives us:
-8+x2=18 and -2+y2=8.
Finally, adding 8 to both sides of the equation on the left and 2 to both sides of the equation on the right gives us x2=26 and y2=10.
Therefore, the other end point is (26, 10).
