Multiplication by a Scalar -Explanation and Examples

Multiplication by a scalar is a way of changing the magnitude or direction of a vector.  Put, it is

Recall that a scalar is just a real number. Multiplying a vector by a scalar causes a change in the scale of that vector.

In this topic, we will discuss the following aspects of scalar multiplication:

• What is Scalar Multiplication?
• How to Multiply a Vector by a Scalar?
• Multiplying a Vector by a Scalar

What is Scalar Multiplication?

Scalar multiplication involves multiplying a given quantity by a scalar quantity. If the given quantity is scalar, the multiplication yields another scalar quantity. But, if the quantity is a vector, multiplication with a scalar gives a vector output.

For example, the multiplication of a scalar C with a vector A will yield another vector. We write this operation as:

C*A   = CA

In the above example, the resultant vector CA is the scaled version of vector A whose magnitude is C times the magnitude of the original vector A. Its direction is determined by the value of C in the following way:

• If C > 0, then the resultant vector CA will have the same direction as the vector A.
• If C <0, then the resultant vector is:
  -C*A   = –CA
  The negative sign will reverse the direction of the resultant vector relative to the reference vector A.
• If C = 0,  then the multiplication yields a zero vector as:
  0*A   = 0

Note that if C = 1, then multiplying any vector by C keeps that vector unchanged.

1*A = A

How to Multiply a Vector by a Scalar?

Suppose a vector P is expressed as the column vector:

P = (x1, y1).

Multiplying it by a scalar means scaling each component of the vector P by C as follows:

C*P = C (x1, y1)

C*P =  (Cx1, Cy1)

Now, the magnitude of the resultant vector can be found in the same way that we can find the magnitude of the vector P:

|C*P| = √(Cx1)^2 + (CX2)^2

Multiplying a Vector by a Scalar

In this section, we will discuss some important properties of scalar multiplication. Note that these properties are true whether a scalar is multiplied by a vector or by another scalar.

Let’s first consider two vectors, A and B, and two scalars, c, and d. Then the following properties hold:

1. |cA| = |c|*|A|. The magnitude of the resultant scaled vector is equal to the absolute value of the scalar times the magnitude.
2. Associative property: c(dB) = (cd)*B
3. Commutative property: c*A = A*c
4. Distributive property: (c + d)A  = c*A + d*A

                                        d* (A + B) = d*A + d* B

Examples

In this section, we will discuss some examples and their step-by-step solutions in order to help establish a better understanding of scalar multiplication.

Example 1 

A car is moving with a velocity of V = 30 m/s towards the North. Determines the vector that is twice this vector.

Solution

From the given data, we have the following information:

V = 30 m/s  North.

To determine the vector equal to twice this vector, we multiply the given vector by the scalar value 2. This gives us:

2* V = 2 * (30 m/s)

2V = 60 m/s, North

Since the given scalar value is positive, the direction of V is not affected. It does, however, change its magnitude to two times the initial value. Thus, the car will keep moving North with twice its initial velocity.

Example 2

Given a vector S = (2, 3), determine and sketch 2*S. What are the magnitude and the direction of the vector 2S?

Solution

The given vector S is a column vector, and the scalar quantity is 2. Multiplying the vector S by 2 gives us:

2*S = 2* (2, 3)

Multiplying each of the components of the vector S by 2 gives us:

2*S = (2*2, 2* 3)

2*S = (4, 6).

Next, we determine and compare the magnitudes of both the vectors:

|S| = √2^2 + 3^2

|S| = √4 + 9

|S| = √13

The magnitude of vector 2S is :

|2S| = √4^2 + 6^2

|2S| = √16 + 36

|2S| = √52

|2S| = √4*13

|2S| = 2*(√13)

It can be clearly observed from the last equation that the scalar multiplication has resulted doubled the magnitude of the vector S.

The image given below shows the two vectors, S and 2S. It can be seen that the direction of the vector 2S is parallel to that of the vector S. This further verifies that scaling a vector by a positive quantity only changes the magnitude and does not change the direction.

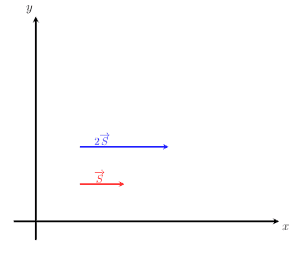
Example 3

Given a vector S = (2, 3), determine and sketch -2*S. Find the magnitude and direction of the vector -2S.

Solution

The given vector S is a column vector, and the scalar quantity is 2. Multiplying the vector S by 2 gives us:

-2*S = -2* (2, 3)

Multiplying each of the components of the vector S by 2 gives us:

-2*S = (-2*2, -2* 3)

-2*S = (-4, -6).

Next, we determine and compare the magnitudes of both the vectors:

|S| = √2^2 + 3^2

|S| = √4 + 9

|S| = √13

The magnitude of vector -2S is :

|-2S| = √(-4)^2 + (-6)^2

|-2S| = √16 + 36

|-2S| = √52

|-2S| = √4*13

|-2S| = 2*(√13)

It can be clearly observed from the last equation that the scalar multiplication has doubled the magnitude of the vector S. Also, the negative sign has no impact on the magnitude of the vector -2S.

The image given below shows the two vectors S and -2S. It can be seen that the direction of the vector -2S is opposite that of the vector S. This further verifies that scaling a vector by a negative quantity does not affect its magnitude (i.e., vectors 2S and -2S have the same magnitude) but does reverse the direction.

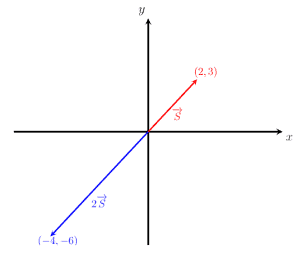
Example 4

Given a vector A = (-4, 6), determine and sketch the vector 1/2*A.

Solution

The given vector A is a column vector, and the scalar quantity is 1/2. Multiplying the vector A by 1/2 gives us:

1/2*A = 1/2* (-4, 6).

Simplifying gives us:

1/2*A = (1/2*(-4),1/2*(6))

1/2*A = (-2, 3).

Next, we determine and compare the magnitudes of both vectors:

|A| = √-4^2 + 6^2

|A| = √16 + 36

|A| = √52

|A| = 2*(√13)

The magnitude of vector 1/2A is :

|1/2A| = √-2^2 + 3^2

|1/2A| = √4 + 9

|1/2A| = √13

Multiplication by a scalar with a value of one half thus decreased the magnitude of the original vector by one half.

The image given below shows the two vectors A and ½ A. Both vectors have the same direction but different magnitudes.

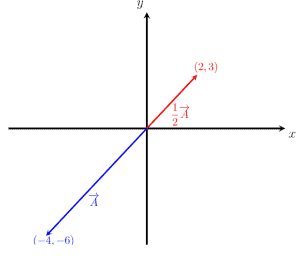
Example 5

Given a vector m = 5i + 6j +3 in the orthogonal system, determine the resultant vector if m is multiplied by 7.

Solution

In this scenario, the resultant vector can be obtained by simply multiplying the given vector by 7:

7m = 7 *(5i + 6j +3)

7m = (7*5i + 7*6j + 7*3)

7m = 35i + 42j + 21

The resultant vector has a 7 times greater magnitude than the original vector m but no change in direction.

Practice Questions

1. Given a vector M = 10 m East, determine the resultant vector obtained by multiplying the given vector by 3.
2. Given a vector N = 15 m North, determine the resultant vector obtained by multiplying the given vector by -4.
3. Let u = (-1, 4). Find 5u.
4. Let v = (3, 9). Find -1/3v.
5. Given a vector b = -3i + 2j +2 in the orthogonal system, find 5b.

Answers

1. 3M = 30 m, East.
2. -4N = -60 m, South.
3. 5u = (-5, 20), |u| = √17, |5u| = 5*√17. The direction of u and 5u is the same.
4. -1/3v = (-1, -3), |v| = 3*√10, |-1/3v| = √10, the direction of the vector -1/3v is opposite to the direction of the vector v.
5. 5b = -15i + 10j + 10

Previous Lesson | Main Page | Next Lesson