Multiplication Property of Equality – Examples and Explanation

The multiplication property of equality states that equality holds when the products of two equal terms are multiplied by a common value.

This is the same as the multiplicative property of equality. It is important in both arithmetic and algebra.

Before moving on with this section, make sure to review the general article on properties of equality.

This section covers:

• What Is the Multiplication Property of Equality?
• Multiplication Property of Equality Definition
• Converse of the Multiplication Property of Equality
• Is the Multiplication Property of Equality an Axiom?
• Example of the Multiplication Property of Equality

What Is the Multiplication Property of Equality?

The multiplication property of equality applies when two terms are equal. After they are multiplied by a common term, they are still equal.

Note that it is also sometimes called the multiplicative property of equality.

This fact is used in arithmetic to find equal terms. In algebra, the multiplicative property of equality helps to isolate an unknown term. This is because division is the opposite of multiplication.

Multiplication Property of Equality Definition

If equal terms be multiplied by equal quantities, the products are equal.

In simpler language, multiplying two sides of an equation by the same term does not change the equality.

The arithmetic definition is:

If $a=b$, then $ac=bc$ (where $a, b,$ and $c$ are all real numbers).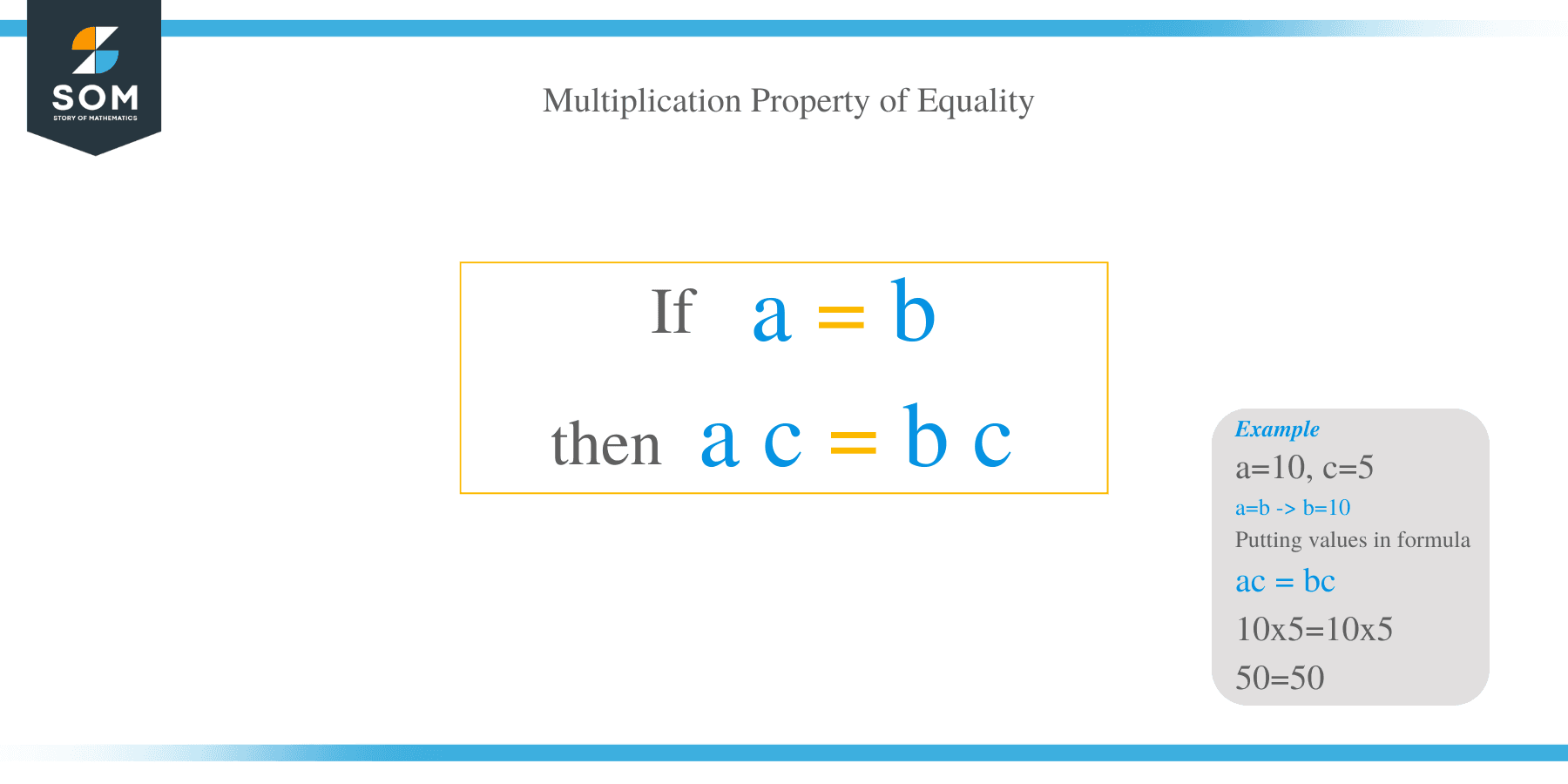

Converse of the Multiplication Property of Equality

Note that the converse is also true. That is, let $a, b,$ and $c$ be real numbers. If $a\neq b,$ then $ac\neq bc$.

Is the Multiplication Property of Equality an Axiom?

Euclid wrote about the addition, subtraction, and transitive properties of equality. He called them “common notions” in his Elements. He also wrote a version of the reflexive property of equality as Common Notion 4. However, he did not include multiplication property of equality. This is likely because it does not have as many uses in planar geometric proofs.

In the 1800s, Giuseppe Peano made a list of arithmetic axioms. These were meant to be statements for which no proof was needed. He did not include  multiplication in his list. The list is usually augmented with addition multiplication though.

Peano’s only applied to natural numbers. These are whole numbers greater than $0$. Most axiom lists today hold these properties true for all real numbers.

These facts may seem obvious. Listing them, however, was very important. It ensured mathematical rigor when proof-based math was starting to take off.

The multiplicative property of equality for finite natural numbers can be deduced. It follows from using both the arithmetic property of equality and the substitution property of equality.

Additionally, the multiplication property for $c\neq0$ can be deduced from the division property of equality. Likewise, the division property of equality can be deduced from the multiplication property of equality. Despite that fact, the two are usually listed as two separate axioms.

Example 3 derives the division property of equality from the multiplication property of equality. Practice problem 3 derives a form of the multiplication property from the addition and substitution properties.

Example of Multiplication Property of Equality

Unlike some of the other properties of equality, Euclid did not list the multiplication property of equality as a common notion. Thus, there are not any famous Euclidean proofs that rely on it.

There are, however, lots of uses for the multiplication property of equality. Specifically, any time there is division of a variable, multiplication will isolate the variable.

In algebra, isolating the variable determines its value. For example, if $\frac{x}{4}=6$, then:

$\frac{x}{4}\times4=6\times4$.

This simplifies to $x=24$.

Examples

This section covers common examples of problems involving multiplication property of equality and their step-by-step solutions.

Example 1

Suppose $a=b$ and $c$ and $d$ are real numbers. Which of the following pairs must be equal?

• $ac$ and $bc$
• $ad$ and $bd$
• $ac$ and $dc$

Solution

The first two pairs of products are equal, but the last one is not.

Since $a=b$, multiplying $a$ and $b$ by any common value makes the resulting products equal. Since $c$ is equal to itself, $ac=bc$.

Likewise, since $d$ is equal to itself, $ad=bd$.

While $c$ is equal to itself, $a$ and $d$ are not known to be equal. Therefore, $ac$ and $dc$ are also not known to be equal.

Example 2

At the grocery store, bananas and squash are both 49 cents per pound. Ali buys exactly 5 pounds of each of them. How does the amount Ali spent on bananas compare to the amount he spent on squash?

Example 2 Solution

Let $b$ be the cost of a pound of bananas and let $s$ be the cost of a pound of squash. In this case, $b=0.49$ and $s=0.49$. Thus, $b=s$.

Ali buys five pounds of bananas. Thus he spends $5b$ on bananas.

Likewise, since he buys five pounds of squash, he spends $5s$ on squash.

Since $b=s$, the multiplicative property of equality states that $ab=as$ when $a$ is some number. In this case, $5b=5s$.

That is, Ali will spend the same amount on squash as he will on bananas.

Solving gives:

$5*0.49=2.45$

Thus, Ali spends 2.45 dollars on bananas and 2.45 dollars on squash.

Example 3

Use the multiplication property of equality to deduce the division property of equality.

Example 3 Solution

Let $a, b,$ and $c$ are all real numbers and $a=b$. The multiplication property of equality states that $ac=bc$.

Use this fact to prove the division property of equality. That is, prove that for any real numbers $a, b,$ and $c\neq0$, such that $a=b$, $\frac{a}{c}=\frac{b}{c}$.

Note that $c$ can’t equal $0$. This is because dividing by $0$ is impossible.

Assume the multiplication property of equality holds and that $c\neq0$.

Then $\frac{1}{c}$ is also a real number. Multiply $a$ and $b$ by $\frac{1}{c}$.

$a\times\frac{1}{c}=b\times\frac{1}{c}$

This simplifies to:

$\frac{a}{c}=\frac{b}{c}$

Thus, given the multiplication property of equality and any real number $c\neq0$, the division property holds. That is, let $a, b,$ and $c$ be real numbers such that $a=b$ and $c\neq0$. Then $\frac{a}{c}=\frac{b}{c}$.

Example 4

Let $x$ be a real number such that $\frac{x}{8}=\frac{1}{3}$.

Use the multiplication property of equality to isolate the variable and find the value of $x$.

Example 4 Solution

Since $8$ divides $x$, multiplying $x$ by $8$ isolates the variable.

But, equality only holds when both sides must be multiplied by $8$.

$\frac{x}{8}\times8=\frac{1}{3}\times8$

Simplifying this yields:

$x=\frac{8}{3}$

Therefore, the value of $x$ is $\frac{8}{3}$.

Example 5

Let $x$ and $y$ be real numbers such that $\frac{x}{4}=3z$ and $\frac{y}{2}=6z$.

Use the multiplication property of equality and the transitive property of equality to prove that $x=y$.

Example 5 Solution

First, solve for both $x$ and $y$ by isolating the variables.

If $\frac{x}{4}=3z$, then multiplying both sides by $4$ gives:

$\frac{x}{4}\times4=3z\times4$

This simplifies to:

$x=12z$

Similarly, if $\frac{y}{2}=6z$, then multiply both sides by $2$.

$\frac{y}{2}\times2=6z\times2$

This simplifies to:

$y=12z

Since $x=12z$ and $y=12z$, the transitive property of equality states that $x=y$, as required.