Multiplying Decimals – Explanation & Examples

How to Multiply Decimals?

In this article, we will learn how to carry out multiplication of two decimals as well as multiplication of a decimal number and a whole number. Multiplication of decimal numbers is closely similar to multiplication of integers or whole numbers. There different rules of multiplications of decimals numbers .and whole numbers. Let’s take a look at the rules of multiplying of decimals.

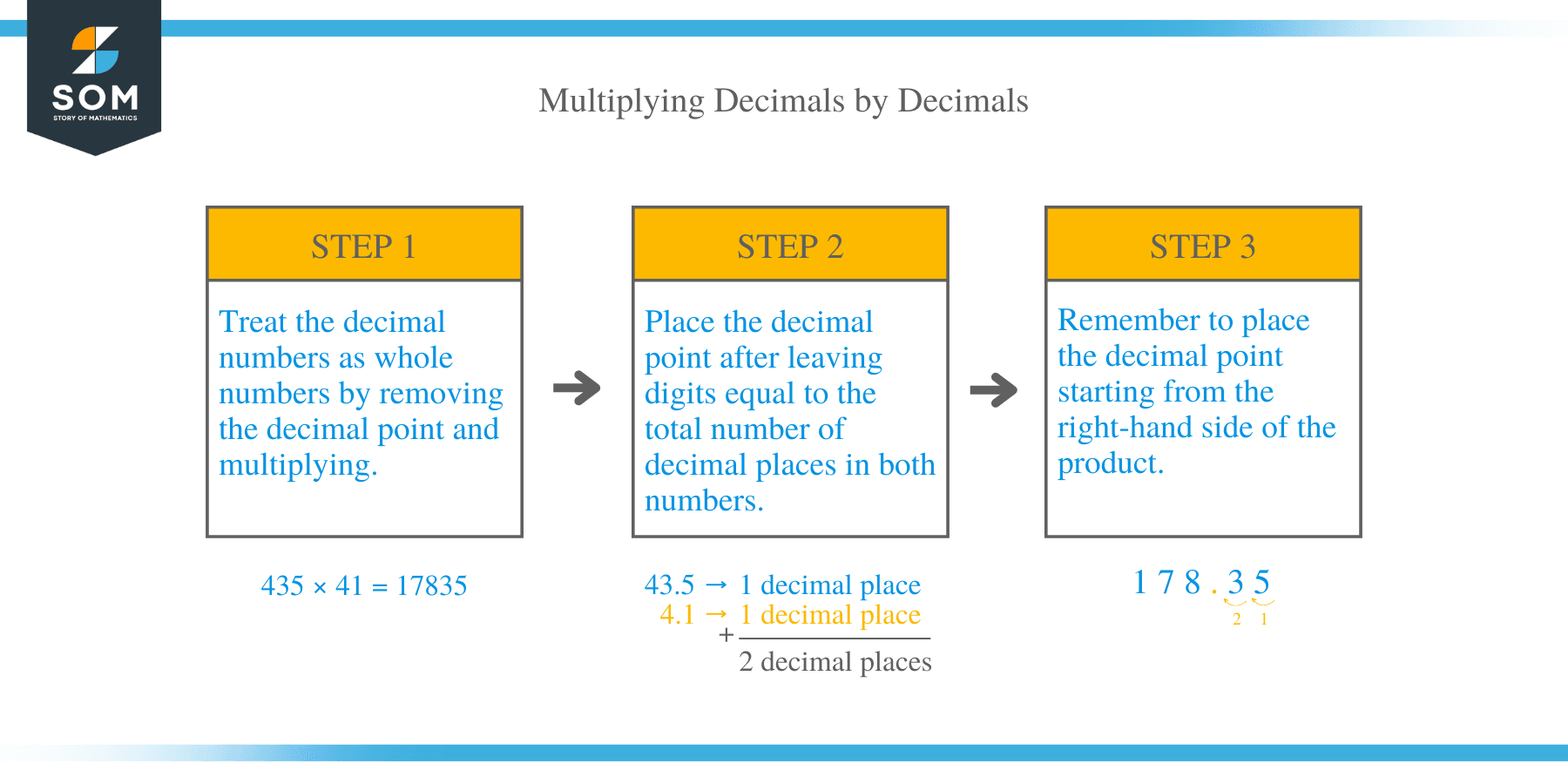
 Multiplying Decimals by Decimals

• Treat the decimal numbers as whole numbers by removing the decimal point and multiply.
• Place the decimal point after leaving digits equal to the total number of decimal places in both numbers.
• Remember to place the decimal point starting from the right-hand side of the product.

Example 1

Multiply: 43.5 × 4.1

• First, perform the multiplication ignoring decimal point.
• Treat the decimals as whole numbers: 435 × 41 = 17835
• Now insert the decimal point in the product (17835) to get as many decimal places in the product as there are in the multiplicands.
• In this case each multiplicand contains one decimal place, and so the total number of decimal places is two. Therefore, place two decimal in the product.
• Therefore, 43.5 × 4.1=178.35

Example 2

Find 81.32 × 8.3

• Treat the decimal numbers as whole numbers and multiply.
• 8132 × 83 = 674956
• In this example, the total number of decimal places in the multiplicands are 3. The decimal number 81.32 contains 2 decimal places and 8.3 contains 1 decimal place. Therefore, the sum of the decimal places in both numbers is 3.
• Place the same number of decimal places in the product as in the totals of multiplicands. Start counting from the right of the product.
• Therefore, 81.32 × 8.3 = 674.956

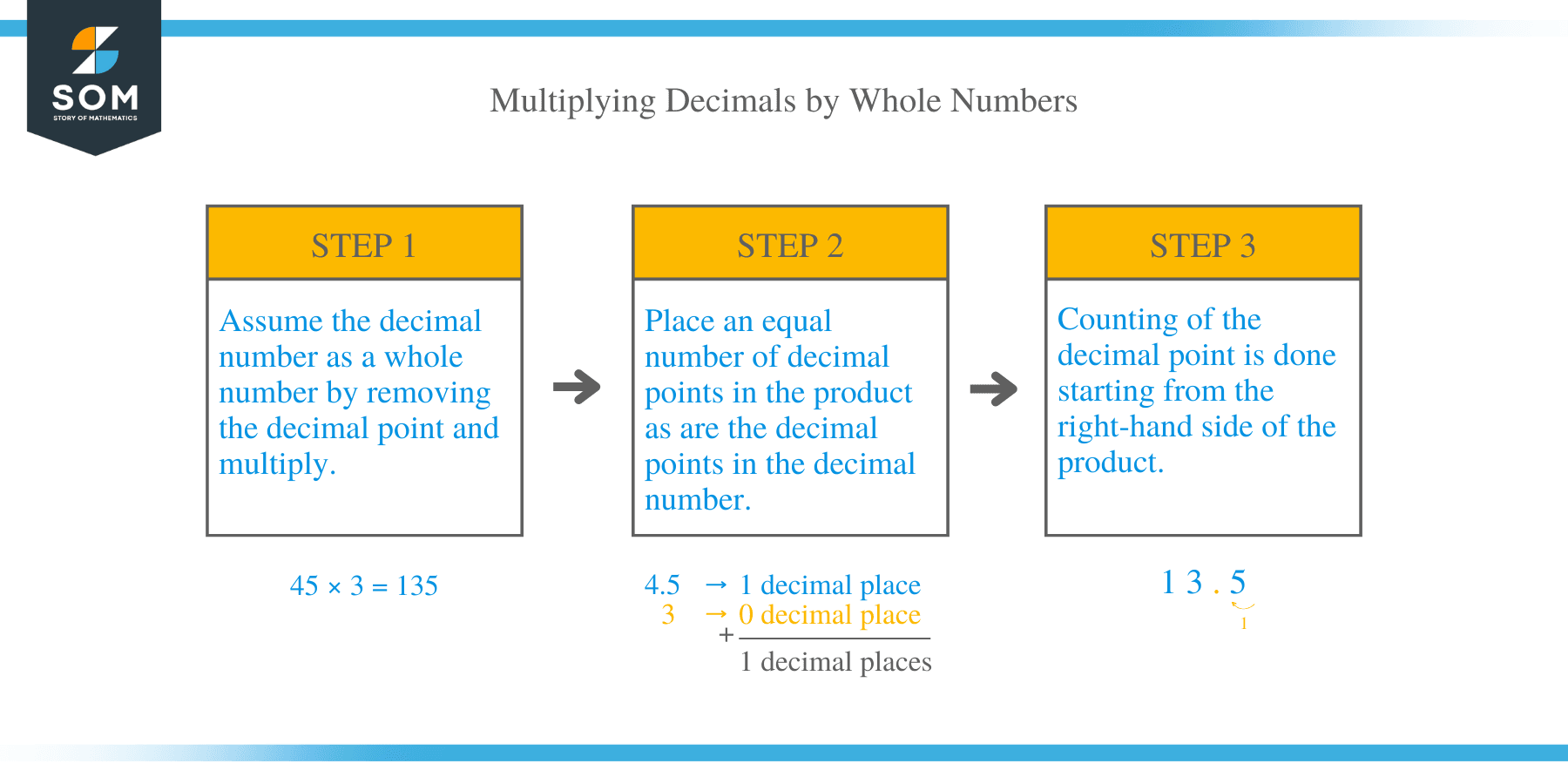
Multiplying Decimals by Whole Numbers

The rules of multiplying a decimal number and a whole number are similar to the rules for multiplying decimals only. The only difference in this case is that, one of the multiplicands is a whole number. These are some of the rules:

• Assume the decimal number as a whole number by removing the decimal point and multiply.
• Place an equal number of decimal points in the product as are the decimal points in the decimal number.
• Counting of the decimal point is done starting from the right-hand side of the product.

Example 3

Calculate 4.5 × 3

• Carryout the multiplication by ignoring the decimal point.
• 45 × 3 = 135
• Place in product an equal number of decimal points as are in the decimal number. Here, the number of decimal places is 1,
• Therefore, 4.5 × 3 = 13.5

Example 4

Find the product of 91.3012 and 83.

• Perform the multiplication operation by ignoring the decimal point.
• 913012 x 83 =
• Place the same number of decimal places as are in the decimal number. Here, the decimal number contains 4 decimal places, and therefore, the product will also contain 4 decimal places.
• The answer is, 7577.9996

Properties of Multiplication of Decimal Numbers

• The product of two decimal numbers remains the same, even if the order of multiplication is changed. For example: 4 × 0.8 = 0.8 × 1.4 = 1.12 and
• The product of a decimal number and 1 is the decimal number itself. For example:

2.519 × 1 = 2.519

• The product of a decimal number with zero is zero. For example: 008 × 0 = 0
• In multiplication of decimal numbers, the order of the groupings can be changed without changing product. For instance:02 × (11.2 × 2.3) = (1.02 × 2.3) × 11.2.
• The product of a whole number and decimal number remains the same when the numbers are multiplied in any order. For example: 1.8 × 11 = 11 × 1.8 = 19.8.