Multiplying Exponents – Explanation & Examples

Exponents are powers or indices. An exponent or power denotes the number of times a number is repeatedly multiplied by itself. For example, when we encounter a number written as, 5³, it simply implies that 5 is multiplied by itself three times. In other words, 5³ = 5 x 5 x 5 = 125.

An exponential expression consists of two parts, namely the base, denoted as b and the exponent, denoted as n. The general form of an exponential expression is b ⁿ.

How to Multiply Exponents?

Performing multiplication of exponents forms a crucial part of higher-level math, however many students struggle to understand how to go about with this operation. Though expressions involving negative and multiple exponents seems confusing.

In this article, we are going to learn multiplication of exponents and therefore, this is going to help you feel much more comfortable tackling problems with exponents.

Multiplication of exponents entails the following subtopics:

• Multiplication of exponents with same base
• Multiplying exponents with different bases
• Multiplication of negative exponents
• Multiplying fractions with exponents
• Multiplication of fractional exponents
• Multiplying variables with exponents
• Multiplication of square roots with exponents

Multiplying exponents with the same base

In multiplication of exponents with the same bases, the exponents are added together. The multiplication rule of adding exponents when the bases are same can be generalized as: a ⁿ x a ^m = a ^{n+ m}

Example 1

• m⁵ × m³ = (m × m × m × m × m) × (m × m × m)

= m^{5 + 3}

= m⁸

• 3⁴ × 3² = (3 × 3 × 3 × 3) × (3 × 3) = 3 ^{4+ 3}= 3⁶
• (-3) ³ × (-3) ⁴ = [(-3) × (-3) × (-3)] × [(-3) × (-3) × (-3) × (-3)]

= (-3) ^{3 +4}

= (-3)⁷

• 5³ ×5⁶
  = (5 × 5 × 5) × (5 × 5 × 5 × 5 × 5 × 5)
  = 5³⁺⁶

= 5⁹

• (-7)¹⁰× (-7) ¹²

= [(-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7)] × [( -7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7)].

= (-7) ²²

Multiplying exponents with different bases

When multiplying two variables with different bases but same exponents, we simply multiply the bases and place the same exponent. This rule can be summarized as:

a ⁿ ⋅ b ⁿ = (a ⋅ b) ⁿ

Example 2

• (x³) *(y³) = xxx*yyy = (x y)³
• 3 ² x 4 ²⁼ (3 x 4)²= 12² = 144

If both the exponents and bases are different, then each number is computed separately and then the results multiplied together. In this case, the formula is given by: a ⁿ ⋅ b ^m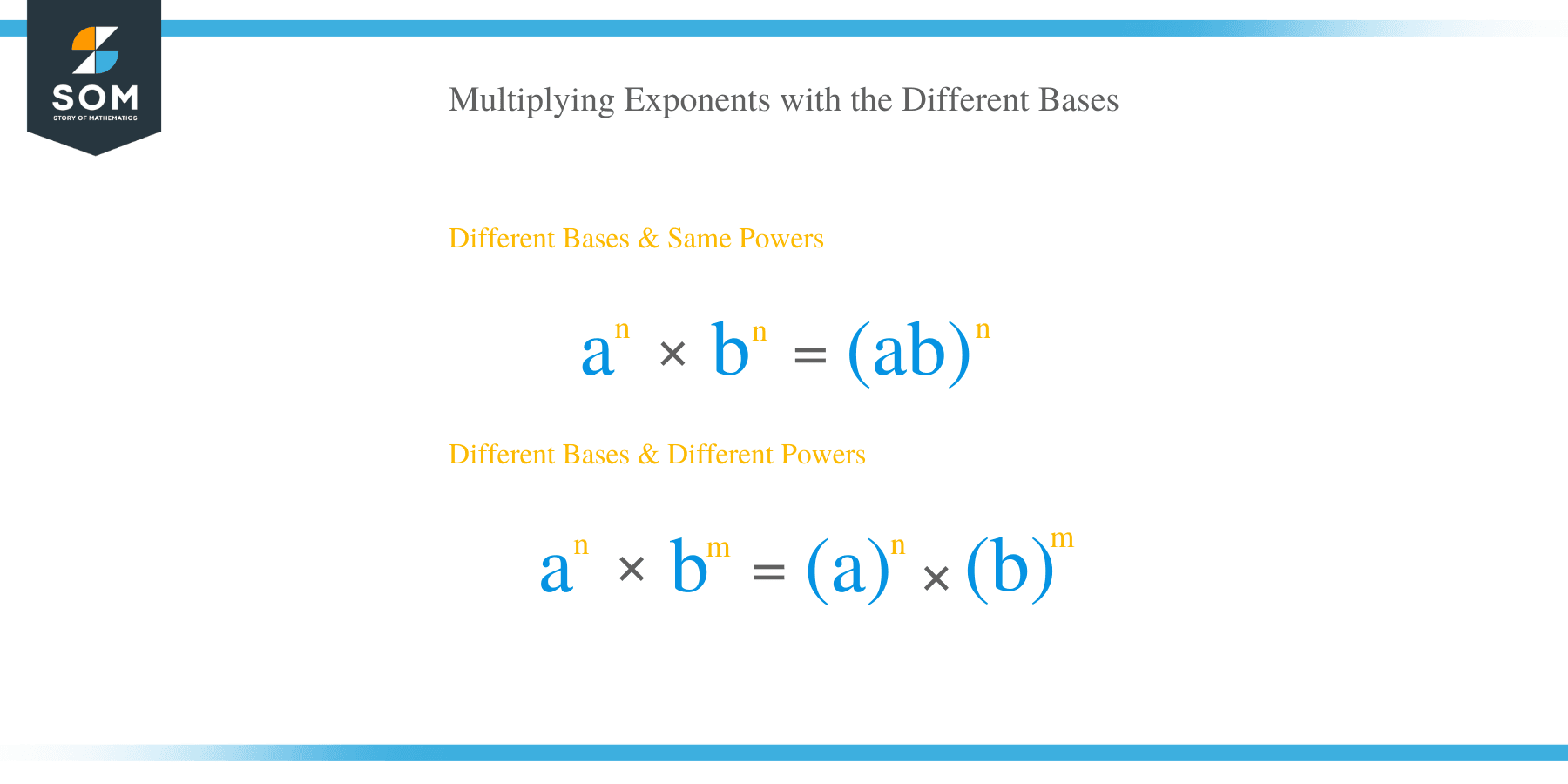

Example 3

• 3²x 4³ = 9 x 64 = 576

• How to multiply negative exponents?

For numbers with the same base and negative exponents, we just add the exponents. In general: a ^-n x a ^-m = a ^{–(n + m)} = 1 / a ^{n + m}.

Example 4

• 2^-3x 2^-4 = 2^-(3+4) = 2^-7 = 1 / 2⁷ = 1 / (2 x 2 x 2 x 2 x 2 x 2 x 2) = 1 / 128 = 0.0078125

Similarly, if the bases are different and the exponents are same, we first multiply the bases and use the exponent.

a ^-n x b ^-n = (a x b) ^-n

Example 5

• 3^-2x 4^-2 = (3 x 4)^-2 = 12^-2 = 1 / 12² = 1 / (12⋅12) = 1 / 144 = 0.0069444

• How to multiply fractions with exponents?

When multiplying fractions with the same base, we add the exponents. For instance:

(a / b) ⁿ x (a / b) ^m = (a / b) ^{n + m}

Example 6

• (4/3)³x (3/5)³ = ((4/3) x (3/5))³ = (4/5)³ = 0.8³ = 0.8 x 0.8 x 8 = 0.512
• (4/3)³x (4/3)² = (4/3) ³⁺² = (4/3) ⁵ = 4⁵ / 3⁵ = 4.214
• (-1/4)^-3× (-1/4)^-2
  (-1/4)^-3 × (-1/4)^-2
  = (4/-1)³ × (4/-1)²
  = (-4)³ × (-4)²
  = (-4) ^{(3 + 2)}
  = (-4)⁵
  = -4⁵
  = -1024.
• (^-2/₇)^-4× (^-5/₇)²
  (^-2/₇)^-4 × (^-5/₇)²
  = (7/-2)⁴ × (-5/7)²
  = (-7/2)⁴ × (-5/7)²
  = (-7)⁴/2⁴ × (-5)²/7²
  = {7⁴ × (-5)²}/{2⁴ × 7² }
  = {7² × (-5)² }/2⁴
  = [49 × (-5) × (-5)]/16
  = 1225/16

• How to multiply fractional exponents?

The general formula for this case is: a ^n/m ⋅ b ^n/m = (a ⋅ b) ^n/m

Example 7

• 2^3/2x 3^3/2 = (2⋅3)^3/2 = 6^3/2 = √ (6³) = √216 = 14.7

Similarly, fractional exponents with same bases but different exponents have the general formula given by: a ^(n/m) x a ^(k/j) = a ^{[(n/m) + (k/j)]}

Example 8

• 2^(3/2)x 2^(4/3) = 2^{[(3/2) + (4/3)]} = 7.127

• How to multiply square roots with exponents?

For exponents with the same base, we can add the exponents:

(√a) ⁿ x (√a) ^m = a ^{(n + m)/2}

Example 9

• (√5)²x (√5)⁴ = 5^(2+4)/2 = 5^6/2 = 5³ = 125

• Multiplication of variables with exponents

For exponents with the same base, we can add the exponents:

xⁿ * x ^m = x ^{n + m}

Example 10

• x²* x³ = (x * x) ⋅ (x * x * x) = x ^{2 + 3} = x ⁵