Multiplying Fractions – Methods & Examples

How to Multiply Fractions?

This article discusses all the steps you need to know about when multiplying fractions, including multiplication of proper and improper fractions, mixed fraction and multiplication of a fraction with a whole number. Here are the steps for multiplication of fractions:

• Multiply the numerators together and place the product on the top of the resultant fraction
• Multiply the denominators together and write the result at the bottom of the new fraction
• Reduce or simplify the result if possible

Example 1:

1/2 × 2/5

Step 1. Multiply the numerators:

1/2 × 2/5  = 1 × 2 = 2

Step 2. Multiply the denominators:

2 x 5 = 10

Step 3. Simplify the fraction:

2/10 = 1/5

Example 2:

1/3 × 9/16

Step 1. Multiply the numerators:

1/3 × 9/16  = 1 × 9 = 9

Step 2. Multiply the denominators:

3 × 16 = 48
Step 3. Simplify the fraction:

9/48 = 3/16

Example 3:

Multiply: 4/5 x 7/9

First multiply the numerators to get: 4 × 7 = 28.

Then multiply the denominators to get: 5 × 9 = 45.

The result= 28/45

Since there are no common factors of 28 and 45, therefore this fraction is already in its lowest terms. The final answer is 28/45.

Example 4:

Multiply: 9/4 x 14/15

You can tackle all the operations in a single line of mathematics. Remember to place the numerator remain on top, and the denominators remain on bottom throughout.

9/4 x 14/15 = (9 x 14)/(4 x 15) = 126/60

Multiplying More than 2 Fractions

Example 5:

Multiply (1/2) × (2/3) × (3/4) × (4/5).

Start by cancelling out common factors.

(1/2) × (2/3) × (3/4) × (4/5).

= 1/5

How to Multiply Fractions with Whole Numbers?

Fractions can be multiplied by whole numbers just the same way other fractions are multiplied. The most important procedure is to rewrite the whole number as a fraction by introducing a denominator of 1. Then, the same methods of multiplying fraction can be applied.

A whole number N can be converted into a fraction whose denominator is 1 as:

N = N/1

Example 6:

Multiply:3/5 × 60.

3/5 × 60 = 3/5 x 60/1

Multiply the numerators:

3 x 60 = 180

Multiply the denominators:

1 x 5 = 5

The result is 180/5, Simplify the answer to lowest possible terms.

180/5 = 36.

How to Multiply Mixed Fractions?

A mixed fraction is a fraction consisting of a whole and fraction part. For example, 7½ is a mixed fraction consisting of a whole number 7 and a fractional part ½.

The following are the key steps when multiplying mixed fractions or a mixed fraction with a proper or improper fraction:

• The first step is to convert all the fractions into improper fraction.
• Multiply the numerators and place the product at the top.
• Multiply the denominators and place the product at the bottom.
• Simplify the result if possible.

Example 7:

Multiply: 2 ⁵/₆ x 3 ¹/₄

Start by converting each mixed fraction to an equivalent improper fraction.

2 ⁵/₆ x 3 ¹/₄ = 17/6 x 13/4 = 221/24

The final answer can be simplified or converted back to a mixed number by division. Converting back to a mixed fraction is just like division with a remainder. The quotient becomes the whole part, and the remainder becomes the new numerator.

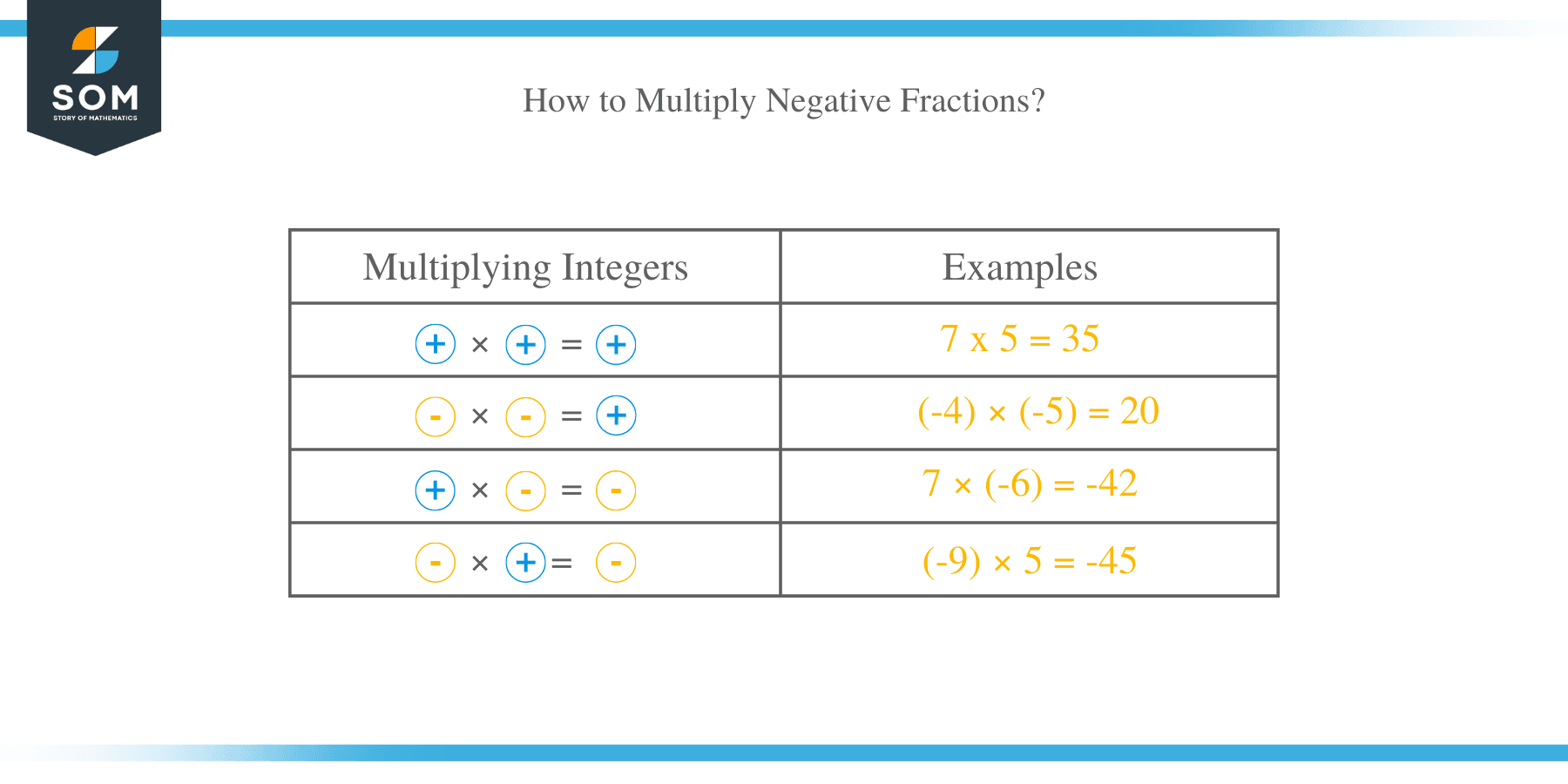
How to Multiply Negative Fractions?

The same rules for multiplying negative numbers are applied when multiplying fractions:

• + x + = +
• + x – = –
• – x – = +

Example 8:

Multiply: 2/3 × (–3/4)

2/3 × (–3/4) = –6/12 = –1/2.

Example 9:

Multiply: (–4/3) × (–7/5)

(–4/3) × (–7/5) = 28/15.