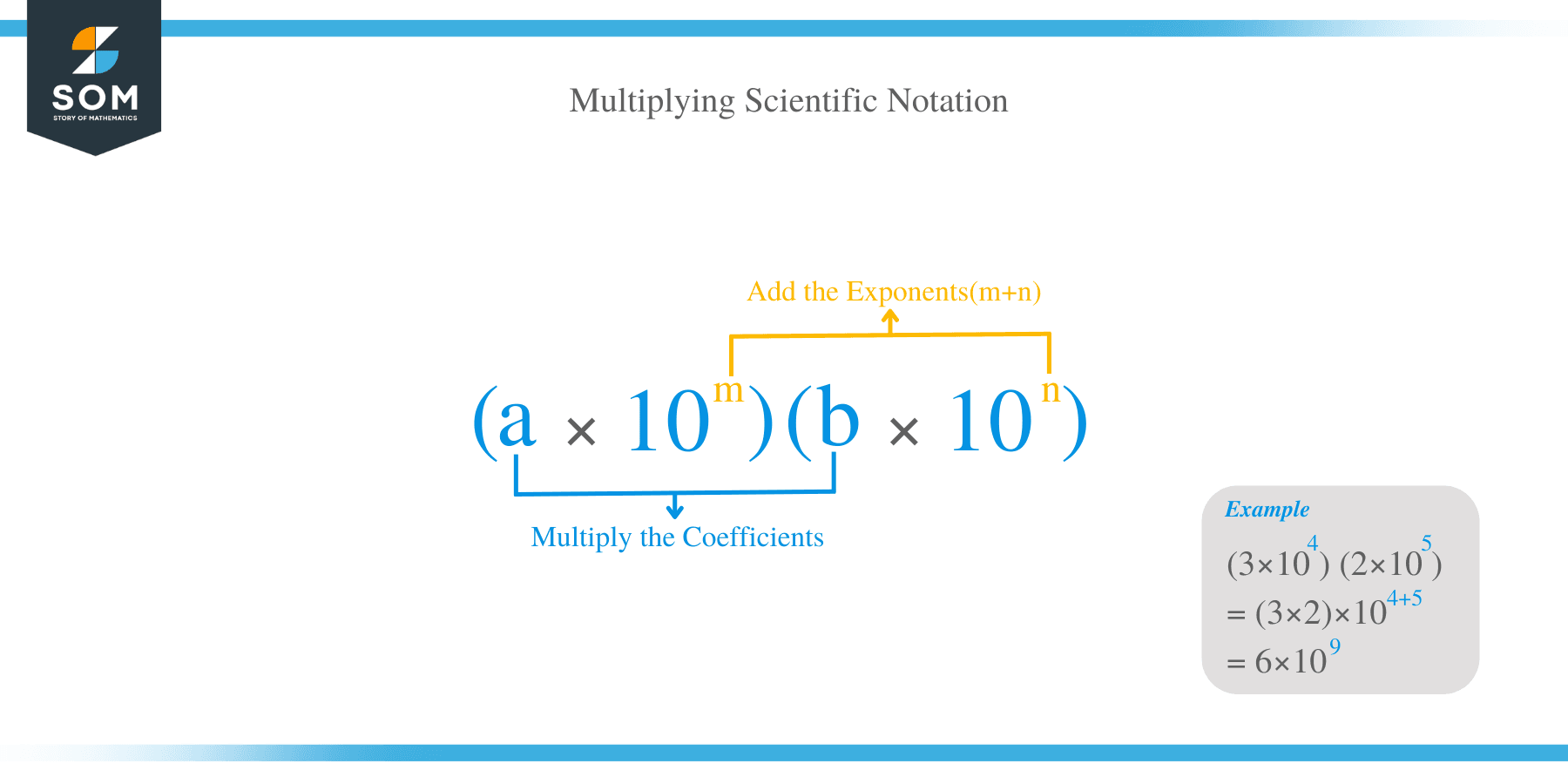Multiplying Numbers in Scientific Notation – Technique & Examples

Extremely small and large numbers can be difficult to record and compute. Consequently, such, significant large and small numbers can be written in a shorter form known as scientific notation.

To write a number in scientific notation, if the given number is greater or equals to 10, the decimal point is moved to the left of the number and so, the power of 10 becomes positive.

For example, the speed of light is said to be 300,000,000 meters per second. This number can be represented into scientific notation as 3.0 x 10 ⁸.

Writing numbers in scientific notation not only simplifies them, but also makes them easier to multiply. In this article, we are going to learn how to carry out the multiplication operation with numbers in scientific notation.

How to Multiply Scientific Notation?

Numbers written in scientific notation can be multiplied simply by taking an advantage of the associative and commutative properties exponents. The associative property is the rule of groupings where for instance, a + (b + c) = (a + b) + c. On the other hand, commutative property states that, a + b = b + a.

To multiply numbers in scientific notation these are the steps:

• If the numbers are not in scientific notation, convert them.
• Regroup the numbers using the commutative and associative properties of exponents.
• Now multiply the two numbers written in scientific notation, you work out the coefficients and the exponents separately.
• Use the product rule; b ^mx b ⁿ = b ^{(m + n)} to multiply the bases.
• Join the new coefficient to the new power of 10 to get the answer.
• If the product of the coefficients is greater than 9, convert it to scientific notation and multiply by the new power of 10.
  

Example 1

Multiply (3 × 10 ⁸) (6.8 × 10 ^-13)

Explanation

• Regroup the numbers considering the associative and commutative properties:
• (3 × 10 ⁸) (6.8 × 10 ^-13) = (3 × 6.8) (10⁸ × 10 ^-13)
• Multiply the coefficients and using the product rule, add the exponents
• (3×6.8) (10⁸ × 10 ^-13) = (20.4) (10 ^{8 – 13})
• The product of the coefficients is 20.4 and is greater than 9, therefore convert it again to scientific notation and multiply by the power of 10.
• (2.04 × 10 ¹) x 10 ^-5
• Multiply using the Product Rule: 2.04×10 ^{1 + ( -5)}
• The answer is 2.04 × 10 ^-4

Example 2

Multiply (8.2 × 10 ⁶) (1.5 × 10 ^-3) (1.9×10 ^-7)

Explanation

• Regroup the commutative and associative properties.
• (8.2 × 1.5 × 1.9) (10 ⁶ × 10 ^-3× 10 ^-7)
• Multiply the coefficients and use the product rule to multiply the bases
• (8.2 × 1.5 × 1.9) (10 ⁶ × 10 ^-3× 10 ^-7) = (23.37) (10 ^{6 + (-3) + (-7)})
• (23.37) (10 ^{6 + (-3) + (-7)}) = (23.37) (10 ^-4)
• The product of coefficient 23. 37 is greater than 9, therefore convert it into scientific notation by moving the decimal point one place to the left and multiply by 10¹.
• (23.37) (10 ^-4) = (2.37 × 10 ¹) × 10 ^-4
• Multiplying using the Product Rule, add the exponents: 2.37 × 10 ^{1 + (-4)}
• Therefore, the answer is 2.37 × 10 ^-3

Example 3

Multiply: (3.2 x 10⁵) x (2.67 x 10³)

Solution

(3.2 x 10⁵) x (2.67 x 10³) = (3.2 x 2.67) x (10⁵ x 10³)

= (8.544) x (10⁵⁺³)

= 8.544 x 10⁸

Therefore, (3.2 x 10⁵) x (2.67 x 10³) = 8.544 x 10⁸

Example 4

Evaluate: (2.688 x 10⁶) / (1.2 x 10²)

Express your answer in scientific notation.

Solution

= (2.688 / 1.2) x (10⁶ / 10²)

= (2.24) x (10^6-2)

= 2.24 x 10⁴

Therefore, (2.688 x 10⁶) / (1.2 x 10²) = 2.24 x 10⁴