Multiplying Radicals – Techniques & Examples

A radical can be defined as a symbol that indicates the root of a number. Square root, cube root, fourth root are all radicals.

Mathematically, a radical is represented as x ⁿ. This expression tells us that a number x is multiplied by itself n number of times.

How to Multiply Radicals?

Radicals quantities such as square, square roots, cube root, etc. can be multiplied like other quantities. The multiplication of radicals involves writing factors of one another with or without multiplication signs between quantities.

For example, the multiplication of √a with √b is written as √a x √b. Similarly, the multiplication n ^1/3 with y ^1/2 is written as h ^1/3y ^1/2.

It advisable to place factors in the same radical sign. This is possible when the variables are simplified to a common index. For example, the multiplication of ⁿ√x with ⁿ √y is equal to ⁿ√(xy). This means that the root of several variables’ product is equal to the product of their roots.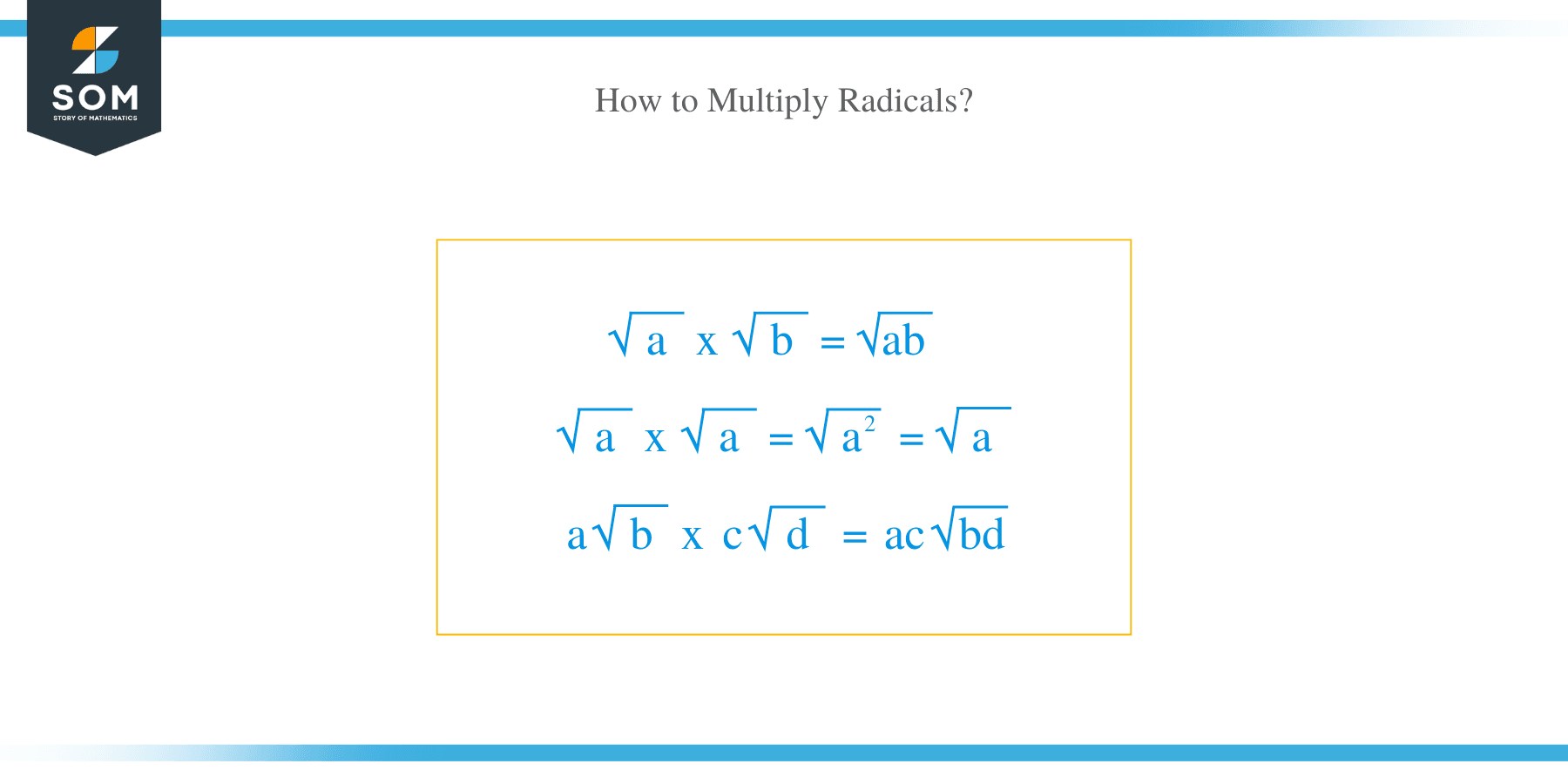

Example 1

Multiply √8xb by √2xb.

Solution

√8xb by √2xb = √(16x ² b ²) = 4xb.

You can notice that the multiplication of radical quantities results in rational quantities.

 

Example 2

Find the product of √2 and √18.

Solution

√2 x √18 = √36 = 6.

Multiplication of Quantities when the Radicands are of the Same Value

Roots of the same quantity can be multiplied by the addition of the fractional exponents. In general,

a ^1/2 * a ^1/3 = a ^{(1/2 + 1/3)} = a ^5/6

In this case, the denominator’s sum indicates the root of the quantity, whereas the numerator denotes how the root is to be repeated to produce the required product.

Multiplication of Radical Quantities with Rational Coefficients

The radicals’ rational parts are multiplied, and their product is prefixed to the product of the radical quantities. For instance, a√b x c√d = ac √(bd).

Example 3

Find the following product:

√12x * √8xy

Solution

• Multiply all quantities the outside of radical and all quantities inside the radical.

√96x ² y

• Simplify the radicals

4x√6 y

Example 4

Solve the following radical expression

(3 + √5)/(3 – √5) + (3 – √5)/(3 + √5)

Solution

• Find the LCM to get,

[(3 +√5)² + (3-√5)²]/[(3+√5)(3-√5)]

• Expand (3 + √5) ² and (3 – √5) ² as,

3 ² + 2(3)(√5) + √5 ² and 3 ²- 2(3)(√5) + √5 ² respectively.

• Add the above two expansions to find the numerator,

3 ² + 2(3)(√5) + √5 ² + 3 ² – 2(3)(√5) + √5 ² = 18 + 10 = 28

• Compare the denominator (3-√5)(3+√5) with identity a ² – b ²= (a + b)(a – b), to get

3 ² – √5 ² = 4

• Write the final answer,

28/4 = 7

Example 5

Rationalize the denominator [(√5 – √7)/(√5 + √7)] – [(√5 + √7) / (√5 – √7)]

Solution

• By calculating the L.C.M, we get

(√5 – √7) ² – (√5 + √7) ² / (√5 + √7)(√5 – √7)

• Expansion of (√5 – √7) ²

= √5 ² + 2(√5)(√7) + √7²

• Expansion of (√5 + √7) ²

= √5 ² – 2(√5)(√7) + √7 ²

• Compare the denominator (√5 + √7)(√5 – √7) with the identity a² – b ² = (a + b)(a – b), to get,

√5 ² – √7 ² = -2

• Solve,

[{√5 ² + 2(√5)(√7) + √7²} – {√5 ² – 2(√5)(√7) + √7 ²}]/(-2)

= 2√35/(-2)

= -√35

 

Example 6

Evaluate

(2 + √3)/(2 – √3)

Solution

• In this case, 2 – √3 is the denominator and rationalizes the denominator, both top, and bottom by its conjugate.

The conjugate of 2 – √3 is 2 + √3.

• Comparing the numerator (2 + √3) ² with the identity (a + b) ²= a ²+ 2ab + b ², the result is 2 ² + 2(2)√3 + √3² =  (7 + 4√3).
• Comparing the denominator with the identity (a + b) (a – b) = a ² – b ², the results is 2² – √3².
• Answer = (7 + 4√3)

Example 7

Multiply √27/2 x √(1/108)

Solution

√27/2 x √(1/108)

= √27/√4 x √(1/108)

= √(27 / 4) x √(1/108)

= √(27 / 4) x √(1/108) = √(27 / 4 x 1/108)

= √(27 / 4 x 108)

Since 108 = 9 x 12 and 27 = 3 x 9

√(3 x 9/ 4 x 9 x 12)

9 is a factor of 9, and so simplify,

√(3 / 4 x 12)

= √(3 / 4 x 3 x 4)

= √(1 / 4 x 4)

=√(1 / 4 x 4) = 1 / 4