Negative Exponents – Explanation & Examples

Exponents are powers or indices. An exponential expression consists of two parts, namely the base, denoted as b and the exponent, denoted as n. The general form of an exponential expression is b ⁿ. For example, 3 x 3 x 3 x 3 can be written in exponential form as 3⁴ where 3 is the base and 4 is the exponent. They are widely used in algebraic problems, and for this reason, it is important to learn them so as to make the studying algebra easy.

Many students will find it hard to understand negative numbers and fractions. It normally a total disaster when negative exponents are added to the equations. Well, not really. Learning negative exponents is a major foundation block for solving advanced mathematical expressions. This is because, it equips students with the necessary skills and knowledge to face challenging problems in and out of the classroom.

If you are wondering where to begin, don’t worry, this article is going to help you transform your course on negative exponents into a positive experience.

To help you understand the negative exponent rule better, this paper discusses in detail the following topics of negative exponent rule:

• Negative exponents rule
• Examples of negative exponents
• Negative fractional exponents
• How to solve Fractions with negative exponents
• How to multiply negative exponents
• Dividing negative exponents

Before we tackle each one of these topics, let us do a quick recap of the rules of exponents.

• Multiplication of powers with same base: With multiplication of like bases, add the powers together.
• Quotient of powers rule: When dividing like bases, the powers are subtracted
• Power of powers rule: Multiply powers together when raising a power by another exponent
• Power of a product rule: Distribute power to each base when raising several variables by a power
• Power of a quotient rule: Distribute power to each base when raising several variables by a power
• Zero power rule: This rule implies that, any base raised to a power of zero is equal to one
• Negative exponent rule: To convert a negative exponent to a positive one, write the number into a reciprocal.

How to Solve Negative Exponents?

The law of negative exponents states that, when a number is raised to a negative exponent, we divide 1 by the base raised to a positive exponent. The general formula of this rule is: a ^-m = 1/a ^m and (a/b) ^-n = (b/a) ⁿ.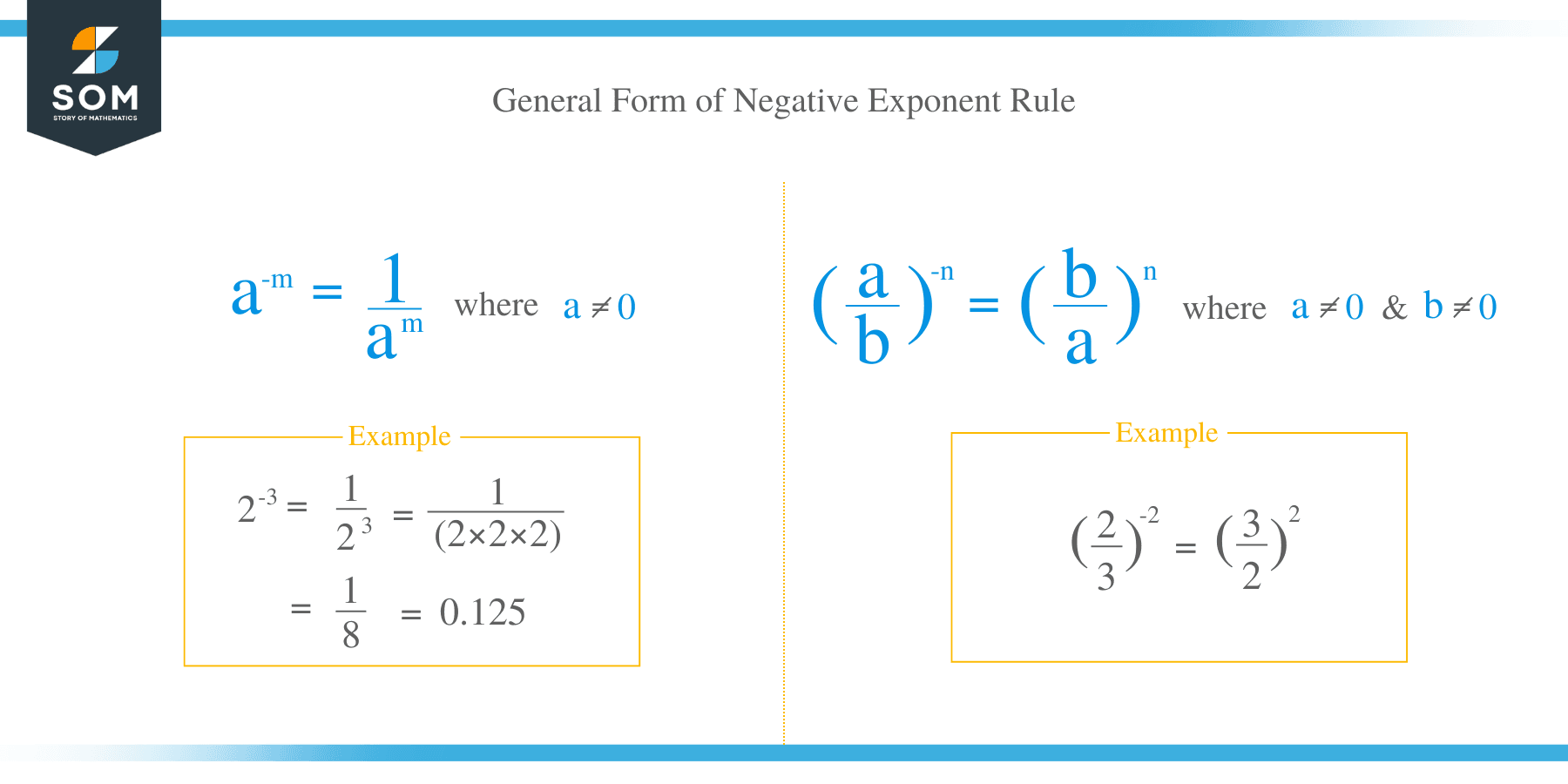

Example 1

Below are examples of how negative exponent rule works:

• 2 ^-3= 1/2 ³ = 1/ (2 x 2 x 2) = 1/8 = 0.125
• 2 ^-2 = 1/2 ² = 1/4
• (2/3) ^-2 = (3/2) ²

Negative fractional exponents

The base b raised to the negative power of n/m is equivalent to 1 divided by the base b raised to the positive exponent of n/m:

b ^-n/m = 1 / b ^n/m = 1 / (^m √b) ⁿ

It implies that, if the base 2 is raised to the negative exponent of 1/2, it is equivalent to 1 divided by the base 2 raised to the positive exponent of 1/2:

2^-1/2 = 1/2^1/2 = 1/√2 = 0.7071

You should notice that a fractional negative exponent is the same as finding the root of the base.

Fractions with negative exponents

The rule implies that, if a fraction a/b is raised to the negative exponent of n, it is equal to 1 divided by the base a/b raised to the positive exponent of n:

(a/b) ^-n = 1 / (a/b) ⁿ = 1 / (a ⁿ/b ⁿ) = b ⁿ/a ⁿ

The base 2/3 raised to the negative exponent of 2 is equal to 1 divided by the base 2/3 raised to the positive exponent of 2. In other words, 1 is divide by the reciprocal of the base raised to a positive exponent of 2

(2/3) ^-2 = 1 / (2/3) ² = 1 / (2 ²/3 ²) = (3/2)² = 9/4 = 2.25

Multiplication of negative exponents

When exponents with the same base are multiplied, we can add the exponents:

a ^-n x a ^-m = a ^{-(n + m) =} 1 / a ^{n + m}

Example 2

2 ^-3 x 2 ^-4 = 2 ^{-(3 + 4)} = 2 ^-7 = 1 / 2 ⁷ = 1 / (2 x 2 x 2 x 2 x 2 x 2 x 2) = 1 / 128 = 0.0078125

In the case of different bases and common exponents of a and b, we can multiply a and b:

a ^-n ⋅ b ^-n = (a ⋅ b) ^-n

Example 3

3 ^-2 x 4 ^{– 2} = (3 x 4) ^-2 = 12 ^-2 = 1 / 12 ² = 1 / (12 x 12) = 1 / 144 = 0.0069444

In case both the bases and the exponents are different we calculate each exponent separately and then multiply:

a ^-n ⋅ b ^-m

Example 4

3^-2 x 4^-3 = (1/9) x (1/64) = 1 / 576 = 0.0017361

How to divide negative exponents

In the case of exponents with the same base, we subtract the exponents:

a ^-n / a^– m = a ^{-n + m}

Example 5

2 ^-6/2 ^-3 = 2 ^-6+3

= 2^-3

= 1/2³

= 1/8