Number Sequence – Explanation & Examples

The number sequence is an essential mathematical tool for testing a person’s intelligence. Number series problems are common in most management aptitude exams.

The problems are based on a numerical pattern that is governed by a logical rule. For example, you might be asked to predict the next number in a given series following the laid rule.

The three prevalent questions in this exam that can be asked are:

1. Identify a term that is wrongly placed in a given series.
2. Find the missing number in a certain series.
3. Complete a given series.

What is a Sequence Number?

Number sequence is a progression or an ordered list of numbers governed by a pattern or rule. Numbers in a sequence are called terms. A sequence that continues indefinitely without terminating is an infinite sequence, whereas a sequence with an end is known as a finite sequence.

Logic numerical problems generally consist of one or two missing numbers and 4 or more visible terms.

For this case, a test designer produces a sequence in which the only one fits the number. By learning and excising number sequence, an individual can sharpen their numerical reasoning capability, which helps our daily activities such as calculating taxes, loans, or doing business. For this case, it is important to learn and practice number sequence.

Example 1

Which list of numbers makes a sequence?

4. 6, 3, 10, 14, 15, _ _ _ _ _ _
5. 4,7, 10, 13, _ _ _ _ _ _

Solution

The first list of numbers does not make a sequence because the numbers lack proper order or pattern.

The other list is a sequence because there is a proper order of obtaining the preceding number. The consecutive number is obtained by adding 3 to the preceding integer.

Example 2

Find the missing terms in the following sequence:

8, _, 16, _, 24, 28, 32

Solution

Three consecutive numbers, 24, 28, and 32, are examined to find this sequence pattern, and the rule obtained. You can notice that the corresponding number is obtained by adding 4 to the preceding number.

The missing terms are therefore: 8 + 4 = 12 and 16 + 4 = 20

 Example 3

What is the value of n in the following number sequence?

12, 20, n, 36, 44,

Solution

Identify the pattern of the sequence by finding the difference between two consecutive terms.

44 – 36 = 8 and 20 – 12 = 8.

The pattern of the sequence is, therefore, the addition of 8 to the preceding term.

So,

n = 20 + 8 = 28.

What are the Types of Number Sequence?

There are many number sequences, but the arithmetic sequence and geometric sequence are the most commonly used ones. Let’s see them one by one.

Arithmetic Sequence

This is a type of number sequence where the next term is found by adding a constant value to its predecessor. When the first term, denoted as x₁, and d is the common difference between two consecutive terms, the sequence is generalized in the following formula:

x_n = x₁ + (n-1) d

where;

x_n is the n^th term

x₁ is the first term, n is the number of terms and d is the common difference between two consecutive terms.

Example 4

By taking an example of the number sequence: 3, 8, 13, 18, 23, 28……

The common difference is found as 8 – 3 = 5;

The first term is 3. For instance, to find the 5^th term using the arithmetic formula; Substitute the values of the first term as 3, common difference as 5, and the n=5

5^th term =3 + (5-1) 5

=23

Example 5

It important to note that the common difference is not necessarily a positive number. There can be a negative common difference as illustrated in the number series below:

25, 23, 21, 19, 17, 15…….

The common difference, in this case, is -2. We can use the arithmetic formula to find any term in the series. For example, to get the 4^th term.

4^th term =25 + (4-1) – 2

=25 – 6

=19

Geometric Series

The geometric series is a number series where the following or next number is obtained by multiplying the previous number by constant known as the common ratio. The geometric number series is generalized in the formula:

x_n = x₁ × r^n-1

where;

x _n = n^th term,

x₁ = the first term,

r =common ratio, and

n = number of terms.

Example 6

For example, given a sequence like 2, 4, 8, 16, 32, 64, 128, …, the n^th term can be calculated by applying the geometric formula.

To calculate the 7^th term, identify the first as 2, common ratio as 2 and n = 7.

7^th term = 2 x 2^7-1

= 2 x 2⁶

= 2 x 64

= 128

Example 7

A geometric series can consist of decreasing terms, as shown in the following example:

2187, 729, 243, 81,

In this case, the common ratio is found by dividing the predecessor term with the next term. This series has a common ratio of 3.

Triangular series

This is a number series in which the first term represents the terms linked to dots presented in the figure. For a triangular number, the dot shows the amount of dot required to fill a triangle. Triangular number series is given by;

x n = (n² + n) / 2.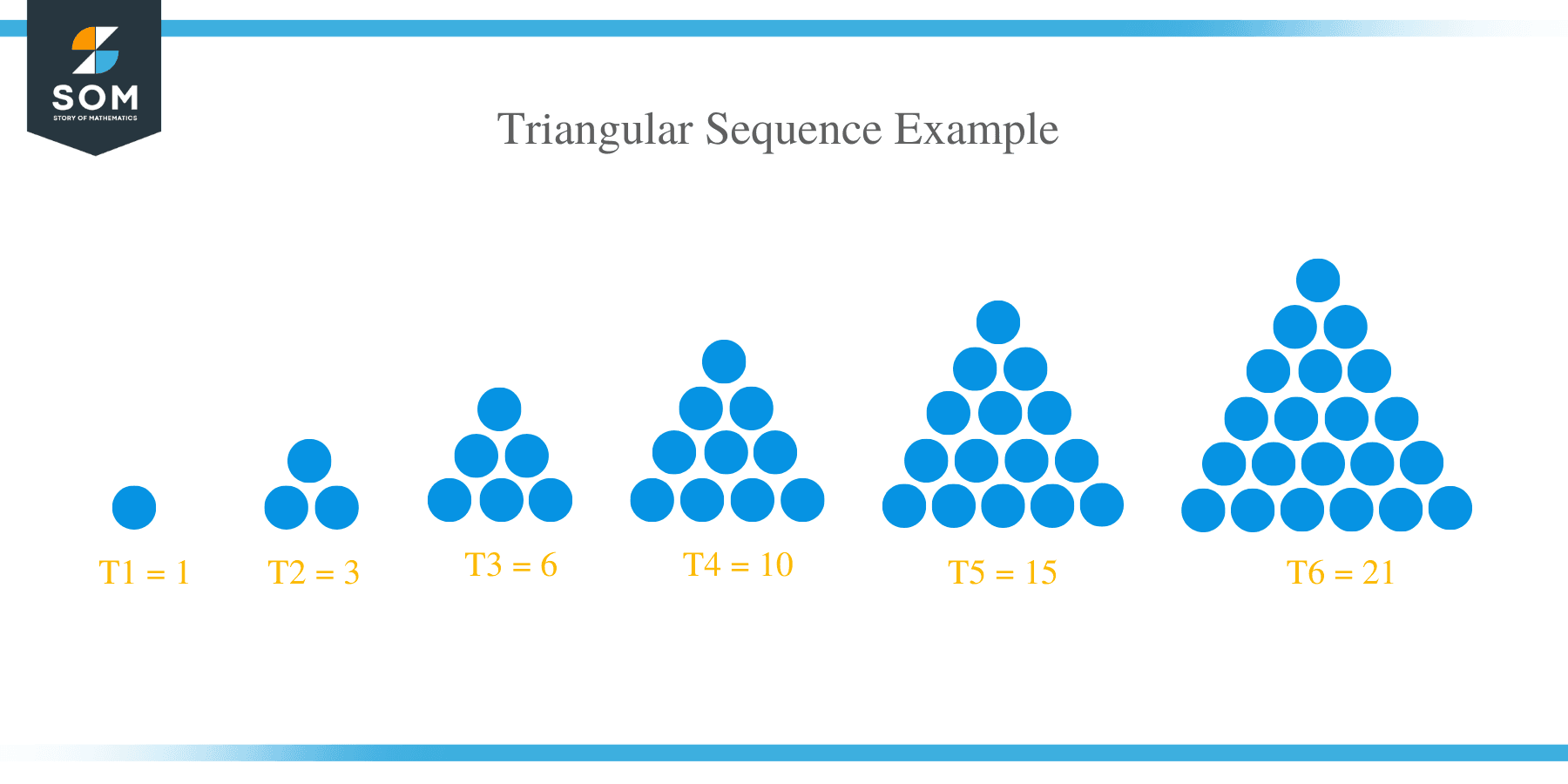

Example 8

Take an example of the following triangular series:

1, 3, 6, 10, 15, 21………….

This pattern is generated from dots that fill a triangle. It is possible to get a sequence by adding dots in another row and counting all the dots.

Square series

A square number is simplifying the product of an integer with itself. Square numbers are always positive; the formula represents a square number of series

x _n = n²

Example 9

Take a look at the square number series; 4, 9, 16, 25, 36………. This sequence repeats itself by squaring the following integers: 2, 3, 4, 5, 6…….

Cube series

Cube number series is a series generated by the multiplication of a number 3 times by itself. The general formula for cube number series is:

x _n = n³

Fibonacci series

A mathematical series consists of a pattern in which the next term is obtained by adding the two terms in-front.

Example 10

An example of the Fibonacci number series is:

0, 1, 1, 2, 3, 5, 8, 13, …

For instance, the third term of this series is calculated as 0+1+1=2. Similarly, the 7^th term is calculated as 8 + 5 = 13.

Twin series

By definition, a twin number series comprises a combination of two series. The alternating terms of twin series can generate another independent series.

An example of the twin series is 3, 4, 8, 10.13, 16, …..By closely examining this series, two series are generated as 1, 3, 8,13 and 2, 4, 10,16.

Arithmetico-Geometric Sequence

This is a series formed by the combination of both arithmetic and geometric series. The difference of consecutive terms in this type of series generates a geometric series. Take an example of this arithmetico -geometric sequence:

1, 2, 6, 36, 44, 440, …

Mixed Series

This type of series is a series generated without a proper rule.

Example 11

For example; 10, 22, 46, 94, 190, …., can be solved using the following steps:

10 x 2= 20 + 2 = 22

22 x 2 = 44 + 2 = 46

46 x 2 = 92 + 2 = 94

190 x 2 = 380 + 2 = 382

The missing term is therefore 382.

Number pattern

Number pattern is generally a sequence or a pattern in a series of terms. For example, the number pattern in the following series is +5:

0, 5, 10, 15, 20, 25, 30………

In-order to solve number pattern problems, closely check the rule governing the pattern.

Try by addition, subtraction, multiplication, or division between consecutive terms.

Conclusion

In summary, problems involving number series and pattern require checking the relationship between these numbers. You should check for an arithmetic relationship such as subtraction and addition. Check for geometric relationships by dividing and multiplying the terms to find their common ratio.