Odd And Even Numbers – Explanation & Examples

What are Odd and Even numbers?

An integer that can be divided by 2 is an even number, while an integer that cannot be divided by 2 is an odd number. They can be either positive or negative. Odd numbers are always in between the even numbers and vice versa.

To differentiate between the odd and even numbers, you always look for their end digit. The last digit of an even number is always 0, 2, 4, 6, or 8, while the last digit of an odd number is always 1, 3, 5, 7, or 9.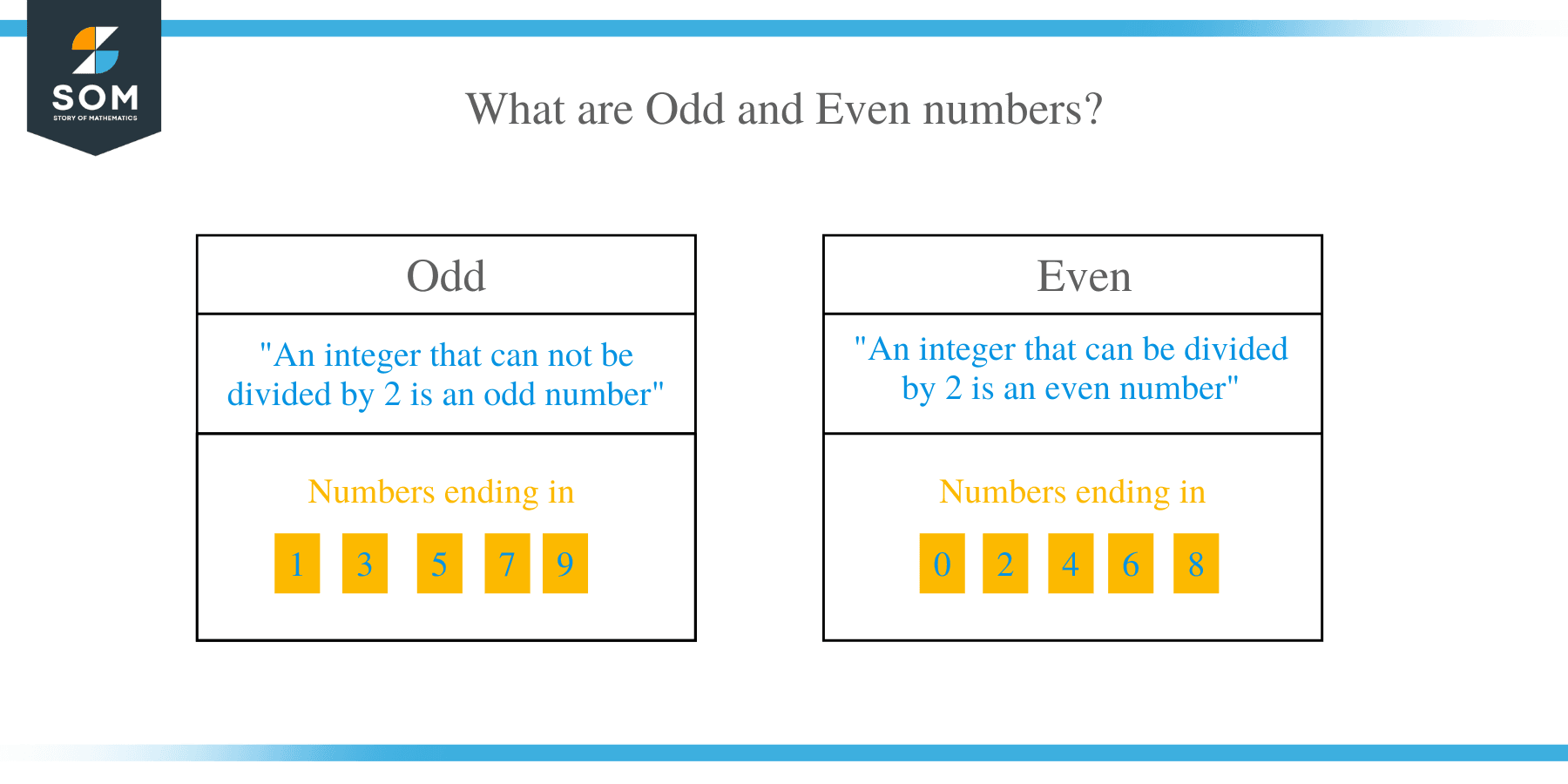

Examples

-22, -10, 0, 6, 18, 234.

The above numbers are even because they end with 0, 2, 4, 6, or 8.

A few examples of odd numbers are:

-101, -17, 1, 9, 23, 985.

The above numbers are odd because they end with 1, 3, 5, 7, or 9.

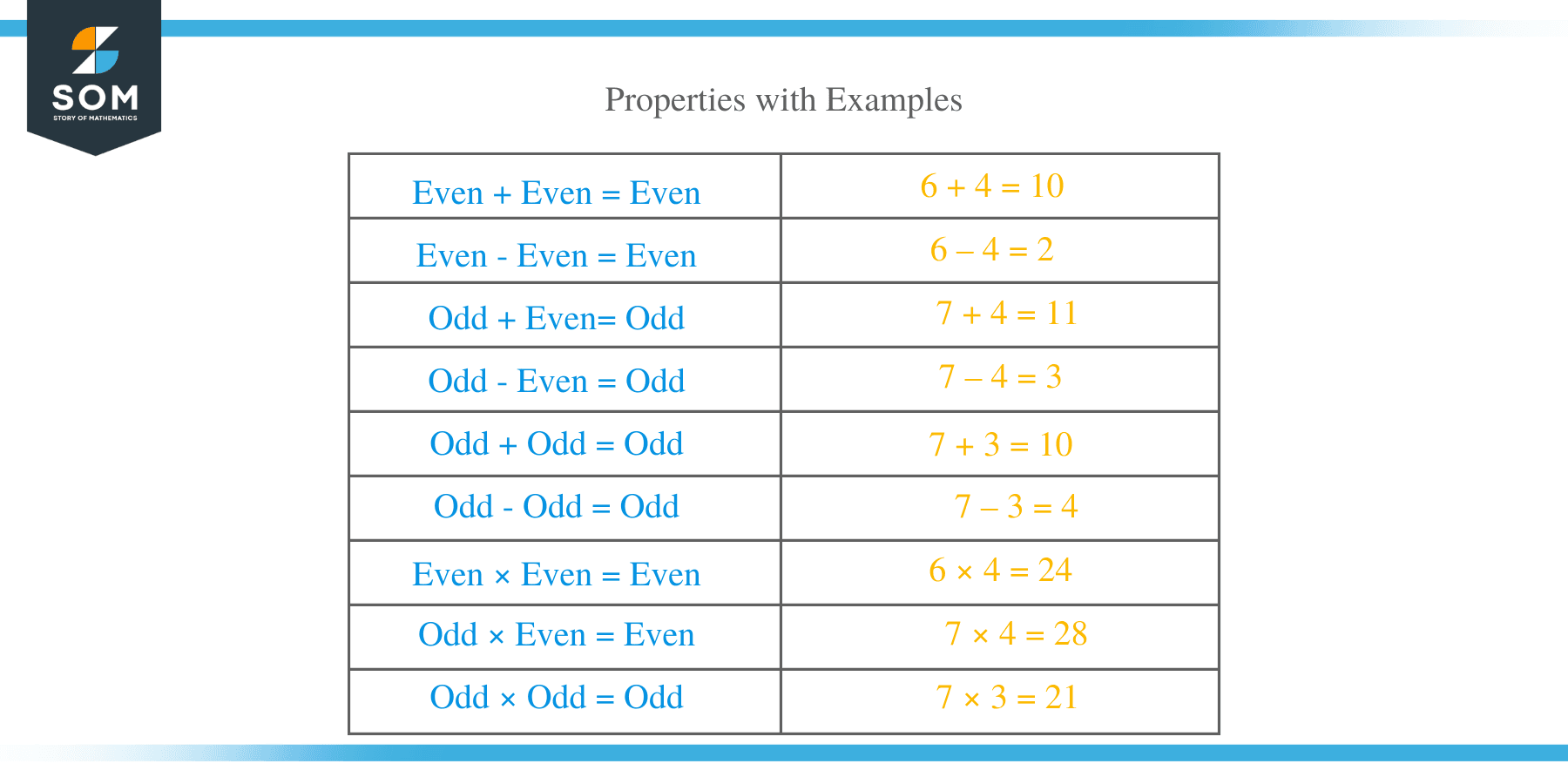
Properties

The odd and even numbers have special properties regarding algebraic operations (addition, subtraction, and multiplication). Whenever we apply algebraic operations to two even or odd numbers, we always get an even or odd number. We exclude division here because the division sometimes gives you the result in fractions while talking about special properties.

• When we add or subtract two even numbers, the result is always an even number.For example,6 + 4 = 10

  6 – 4 = 2

• When we add or subtract an even number and an odd number, the result is always odd.For example,7 + 4 = 11

  7 – 4 = 3

• When we add or subtract two odd numbers, the result is always an even number.For example,7 + 3 = 10

  7 – 3 = 4

• When we multiply two even numbers, the result is always an even number. For example,
  6 × 4 = 24
• When we multiply an even number and an odd number, the result is always an even number. For example,
  7 × 4 = 28
• When we multiply two odd numbers, the result is always an odd number. For example,
  7 × 3 = 21

Generalization of Odd and Even Numbers

We can generalize the even and odd numbers as well. For example, if ‘n’ is an even number, then the next odd number is ‘n + 1’, and the next even number is ‘n + 2’, and so on. Similarly, if ‘n’ is an odd number, then the next even number is ‘n + 1’, and the next odd number is ‘n + 2’, and so on.

For example, if we want to write a series of five odd numbers starting from 73, we can write it as:

73, 73 + 2, 73 + 4, 73 + 6, 73 + 7

73, 75, 77, 79, 81

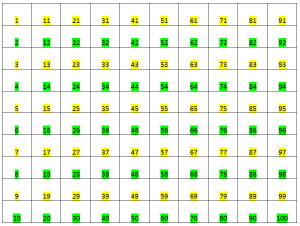
Numbers Chart

The following table is the number chart from 1 to 100, where the odd numbers are highlighted in yellow and the even numbers are highlighted in green.