- Home
- >
- Order of Operations – PEDMAS
JUMP TO TOPIC
Order of Operation– PEMDAS
 Order of operation can be defined as a standard procedure that guides you on which calculations to begin within an expression with several arithmetic operations. Without consistent order of operation, one can make big mistakes during computation.
Order of operation can be defined as a standard procedure that guides you on which calculations to begin within an expression with several arithmetic operations. Without consistent order of operation, one can make big mistakes during computation.
For example, an expression that entails more than an operation such as subtraction, addition, multiplication, or division requires a standard method of knowing which operation to perform first.
For example, if you want to solve a problem like; 5 + 2 x 3, the problem that arises is which operation starts first?
Because this problem has two options of solving it, then which answer is correct?
If we do addition first and then multiplication, the result is:
5 + 2 x 3 = (5 + 2) x 3 = 10 x 3 = 30
If we do multiplication first followed by the addition, the result is:
5 + 2 x 3 = 5 + (2 x 3) = 5 + 6 = 11
To see which one is the correct answer, there is a mnemonic ‘PEMDAS,’ which is useful as it reminds us of the correct order of operations.
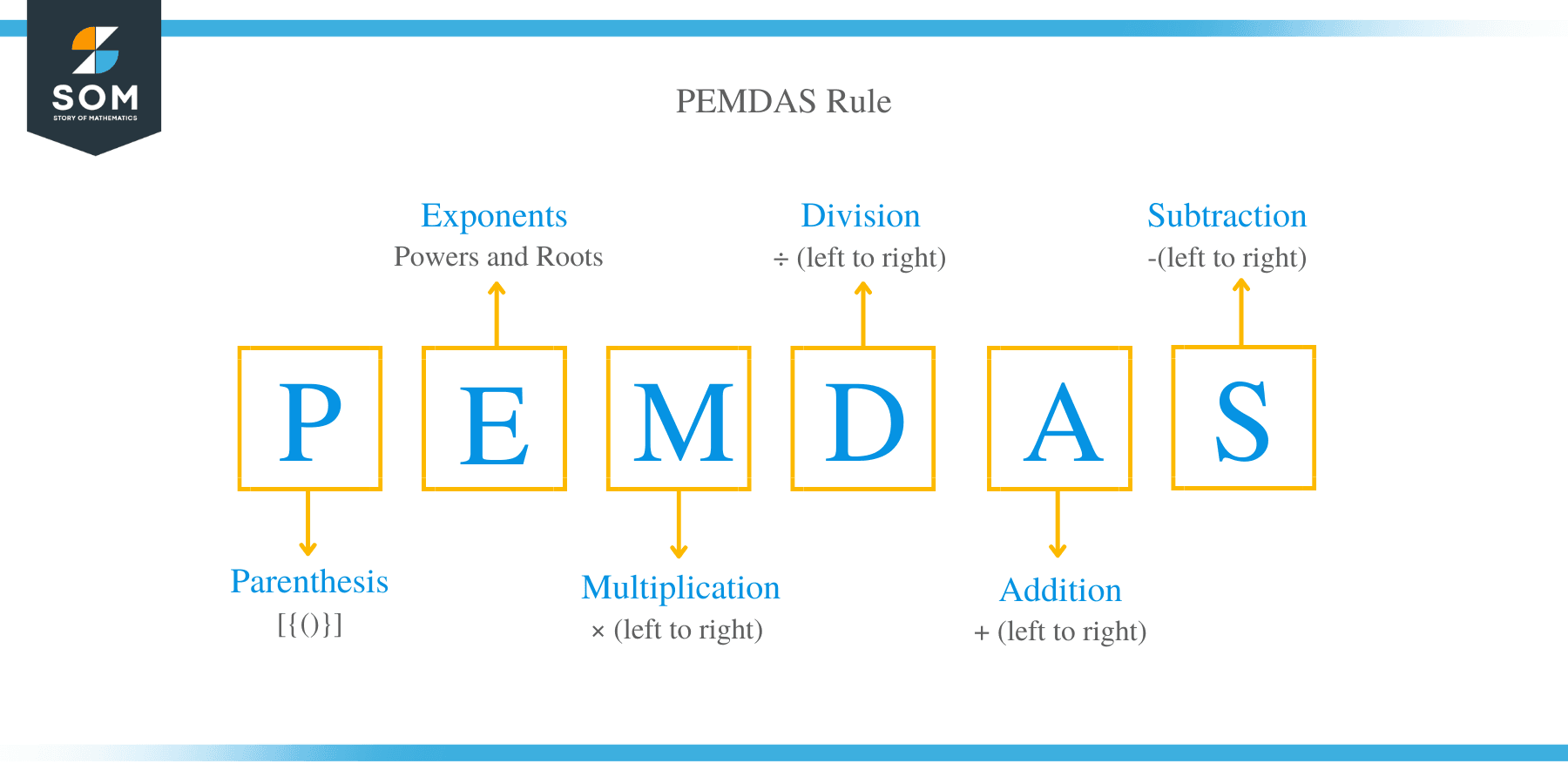
PEMDAS
PEMDAS is an acronym that stands for Parenthesis, Exponents, Multiplication, Addition, and Subtraction. The order of operation is:
- P is for Parentheses: (), brackets [], braces {} and fraction bars.
- E is for Exponent, including roots.
- M is for Multiplication.
- D is for Division.
- A is for Addition.
- S is for Subtraction.

Rules of PEMDAS
- Always start by calculating all expressions within parentheses
- Simplify all the exponents such as square roots, squares, cube, and cube roots
- Perform the multiplication and the division starting from left to right
- Finally, do the addition and subtraction similarly, starting from left to right.
One way of mastering this order of operation is by recalling any of the following three phrases; Choose the one that is easier for you to remember.
- “Please Excuse My Dear Aunt S”
- “Big Elephants Destroy Mice and Snails.”
- “Pink Elephants Destroy Mice and Snails.”
Example 1
Solve
30 ÷ 5 x 2 + 1
Solution
Because there are no parentheses and exponents, start with the multiplication and then division, working from left to right. Finish the operation by addition.
30 ÷ 5 = 6
6 x 2 = 12
12 + 1 =13
NOTE: It is noted that, even though multiplication in PEMDAS comes before division, however, the operation of the two is always from left to right.
Performing the multiplication before the division results in a wrong answer:
5 x 2 = 10
30 ÷ 10 = 3
3 + 1 = 4
Example 2
Solve the following expression: 5 + (4 – 2 ) 2 x 3 ÷ 6 – 1
Solution
- Begin by the parentheses;
(4 – 2) = 2
- Proceed to the exponential operation.
2 2 = 4
- Now we are left with; 5 + 4 x 3 ÷ 6 – 1 = ?
- Perform the multiplication and division, starting from left to right.
4 x 3 = 12
5 + 12 ÷ 6 – 1
Starting from the right;
12 ÷ 6 = 2
5 + 2 – 1 = ?
5 + 2 = 7
7 – 1 = ?
7 – 1 = 6
Example 3
Simplify 3 2 + [6 (11 + 1 – 4)] ÷ 8 x 2
Solution
To work out this problem, PEMDAS is applied as follows;
- Start the operation by tackling the parenthesis.
- Start inside the brackets until all the groupings are eliminated. Addition is done;
11 + 1 = 12
- Perform the subtraction; 12 – 4 = 8
- Work out on the brackets as; 6 x 8 = 48
- Perform the exponents as; 32 = 9
9 + 48 ÷ 8 x 2 = ?
- Work out the multiplication and division from left to right;
48 ÷ 8 = 6
6 x 2 = 12
- 9 + 12 = 21
Example 4
Evaluate the expression; 10 ÷ 2 + 12 ÷ 2 × 3
Solution
By applying the PEMDAS rule, multiplication and division are evaluated from left to right. It is advisable to insert parenthesis to remind yourself of the order of operation
10 ÷ 2 + 12 ÷ 2 × 3
= (10 ÷ 2) + (12 ÷ 2 × 3 )
= 23
Example 5
Evaluate 20 – [3 x (2 + 4)]
Solution
Work out the expressions within the bracket first.
= 20 – [3 x 6]
Work out the remaining parentheses.
= 20 – 18
Lastly, perform subtraction to get 2 as the answer.
Example 6
Work out (6 – 3) 2 – 2 x 4
Solution
- Start by opening the parentheses
= (3)2 – 2 x 4
- Calculate the exponent.
= 9 – 2 x 4
- Now do the multiplication
= 9 – 8
- Finish the operation by subtraction to get 1 as the correct answer.
Example 7
Solve the equation 2 2 – 3 × (10 – 6)
Solution
- Calculate inside the parentheses.
= 2 2– 3 × 4 - Work out the exponent.
= 4 – 3 x 4 - Carry out the multiplication.
= 4 – 12 - Finish the operation by subtraction.
= -8
Example 8
Simplify the expression 9 – 5 ÷ (8 – 3) x 2 + 6 using the order of operations.
Solution
- Work out inside the parentheses
= 9 – 5 ÷ 5 x 2 + 6
- Perform the division
= 9 – 1 x 2 + 6
- Perform the multiplication
= 9 – 2 + 3
- Addition and then subtraction
= 7 + 6 = 13
Conclusion
In conclusion, sometimes, an expression might contain two operations on the same level.
For example, if an expression contains both square and cube, either can be worked out first. Always do the operation from left to right following the PEMDAS rule. If you come across an expression with no grouping symbols such as braces, brackets and parentheses, you can make the operation easier by adding your own grouping symbols.
Working with expressions having fractions are solved by first simplifying the numerator followed by the denominator. The next step is to simplify the numerator and denominator if possible.