• Home
  • >
  • Percentage to Decimal – Conversion Method & Examples

Percentage to Decimal – Conversion Method & Examples

Percentage to DecimalIn mathematics, a percent is simply a number or a ratio expressed out of 100. The term originates from a Latin word –per centum which means by a hundred.

Percent is represented by a symbol (%) known as percentage. Some abbreviations such as “pct.” and “pc” are also used to denote percent. Percent is dimensionless, implying that it has no dimensions. For instance, 20% simply means, 20 per 100 or 20/100.

Percentages are sometimes expressed in decimal and fractional form. For example, 0.6%, 0.25%, 4/5%, 1/2% etc.

How to Convert Percent to Decimal?

Conversion of numbers from percentages to decimals is a helpful mathematics skill every individual should be comfortable with. Percentages and decimals are common in our daily life such as transactions that deal with money and also calculation scores. In academics, students’ scores are calculated in terms of percentages.

For instance, if a student scored 78% of marks in his final exam, then the percentage is calculated basing on the total marks scored by the student to the total marks.


Other applications of percent include:

  • Financial institutions such as banks charge interest on loans in form of percent
  • Companies describe their profit or loss in terms of percent
  • Discounts on commodities are expressed as a percent
  • Salesperson earn commission inform of percent.

For these reasons, it also important to learn how to convert percentages to decimals.

Below are the steps involved when converting numbers from percentages to decimals:

  • Identify the percentage which is to be converted into decimal
  • Remove the percentage sign (%) and divide the number by 100.
  • Convert the resultant fraction into a decimal.
  • Alternatively, you remove the percentage sign (%) and move the decimal two places to the left and right if the number is whole and decimal respectively. For example, to convert 250% to decimals. Move the decimal point two places to the left of the number: 250. → 25. → 2.5. And so, the answer is 2.5

How to convert percent that is a whole number to decimal?

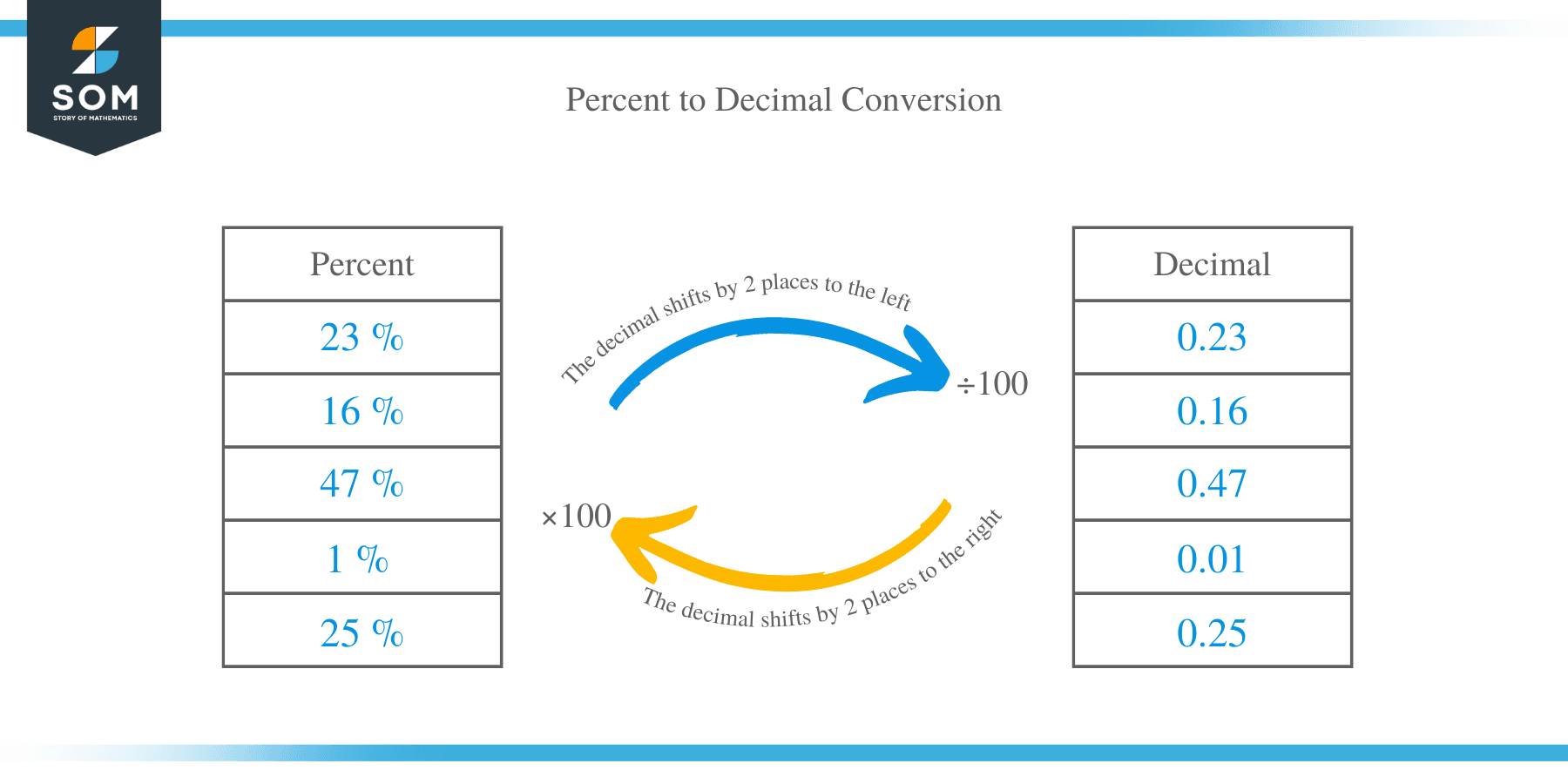
In the case of whole number, the decimal shifts by 2 places to the left.

Example 1

  • 23 % = 23/100 = 0.23
  • 16 % = 16/100 = 0.16
  • 47 % = 47/100 = 0.47
  • 1 % = 1/100 = 0.01
  • 25 % = 25/100 = 0.25
  • 1% = 1 / 100 = 0.01How to Convert Percent to Decimal?

How to convert decimal percent to decimal?

Example 2

  • 75 % = 1.75/100 = (1.75 × 100)/ (100 × 100) = 175/10000 = 0.0175
  • 5 % = 7.5/100 = (7.5 × 10)/ (100 × 10) = 75/1000 = 0.075
  • 5 % = 31.5/100 = (31.5 × 10)/ (100 × 10) = 315/1000 = 0.315
  • 18 % = 0.18/100 = (0.18 × 100)/ (100 × 100) = 18/10000 = 0.0018
  • 2 % = 231.2/100 = (231.2 × 10)/ (100 × 10) = 2312/1000 = 2.312

How to convert fractional percent to decimal?

Example 3

  • 4/5 % = 0.8 % = 0.8/100 = (0.8 × 10)/ (100 × 10) = 8/1000 = 0.008
  • 9/20 % = 0.45 % = 0.45/100 = (0.45 × 100)/ (100 × 100) = 45/10000 = 0.0045
  • 1/80 % = 0.0125 % = 0.0125/100 = (0.0125 × 10000)/ (100 × 10000) = 125/1000000 = 0.000125
  • 13/50 % = 0.26 % = 0.26/100 = (0.26 × 100)/ (100 × 100) = 26/10000 = 0.0026
  • 44/5 % = 8.8 % = 8.8/100 = (8.8 × 10)/ (100 × 10) = 88/1000 = 0.088

 

Practice Questions

1. Which of the following shows the decimal form of $8\%$?

2. Which of the following shows the decimal form of $3 \dfrac{1}{5}\%$?

3. Which of the following shows the decimal form of $108\%$?

4. Which of the following shows the decimal form of $128.8\%$?

5. Which of the following shows the decimal form of $95\%$?

6. Which of the following shows the decimal form of $45\%$?

7. Which of the following shows the decimal form of $29.2\%$?

8. Which of the following shows the decimal form of $0.008\%$?

9. Which of the following shows the decimal form of $142\%$?

10. Which of the following shows the decimal form of $2.85\%$?

11. Suppose that a number is increased by $30\%$ and then the resulting number is decreased again by $20 \%$. What is the total percentage change of the number?

12. The cost of television is reduced from $\$8600$ to $\$7800$. In the nearest two decimal palces, by how much did the price of television reduce?

13. Christine bought a plot of land with an area of $4000$ squared meters. If she plans to use $2400$ squared meters of the land to construct an apartment complex, which of the following shows the percentage (in decimals) of unused land?

14. The population of a city grew from $200000$ to $267000$ in one year. What is the percentage change of the population count in decimals?

15. Annie runs a convenience store. She noticed that the price of beans has increased from $\$8.00$ per kg to $\$12.00$ per kg within two years. What is the percentage increase of the bean’s price as observed by Annie?

16. Alice runs a fruit shop and just received her restock of $400$ apples and $200$ bananas. Upon close inspecting, $12\%$ of apples and $24\%$ of bananas were rotten. In decimal, how much of the fruits are in good condition?


 

Previous Lesson | Main Page | Next Lesson