Polygons – Explanation & Examples

Have you heard about a polygon? Well, polygons are all around us! Most of the common shapes that you see or study every day are polygons. You see a wall, which is rectangular in shape, is a polygon.

A front view of a dice, which has a square shape, is a polygon. A pizza slice is triangular in shape, hence, a polygon.

In this article, you will learn:

What polygons are, and how do they look like.
The different types of polygons.

What is a Polygon?

In mathematics, a polygon is a closed two-dimensional figure made up of line segments but not curves. The term polygon originates from the Greek word “poly -” meaning “many” and “- gon,” meaning “angles.”

The most common examples of polygons are the triangle, the rectangle, and the square. In simple words, polygons are plain figures or shapes made up of line segments only.

Note: Circles, three-dimensional objects, any shapes that include curves, and any shapes that aren’t closed are not polygons.

Polygons were known to human beings since ancient times. Greeks studied non-convex regular polygon in 7^th century BC on a krater by Aristophanes. Thomas Bradwardine was the first known person to study non-convex polygons in the 14^th century. The concept of polygons was generalized in 1952 by Geoffrey Colin.

Now that you have understood what a polygon is let us explore the different polygons and how they look.

Types of Polygons

Depending on the sides and angles, the polygons are classified into different types, namely,

Regular Polygon
Irregular Polygon
Convex Polygon
Concave polygon

Regular Polygon

A regular polygon is a polygon in which all the interior angles are equal, and also, all the sides are equal. There are different types of regular polygons.

These are:

A triangle: An equilateral triangle is a regular polygon with three equal side lengths and three equal angles.

A quadrilateral. A quadrilateral is a regular polygon with four angles and four sides. Examples of quadrilaterals are:

a. A square: A quadrilateral whose 4 sides are equal and four angles are all 90 degrees each.

b. A rectangle:

c. Parallelogram: Opposite sides are parallel, opposite sides are equal in length, opposite angles are equal

d. Kite: Two pairs of adjacent sides are of equal length; the shape has an axis of symmetry.

e. Rhombus: A special type of parallelogram in which all four sides are the same length, like a square that has been squashed sideways.

Pentagon: A polygon that has 5 equal sides and angle

Hexagon: A regular polygon that has 6 equal sides and 6 equal angles.

Heptagon: A regular polygon with 7 equal side lengths and 7 same angles.

Octagon: An octagon has 8 equal sides and 8 equal angles. The best real-life example of an octagon is the STOP road sign.

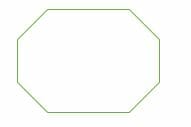
Nonagon: Has 9 equal sides and 9 same angles.

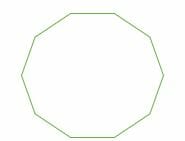
Hendecagon: Has 11 equal sides and 11 equal angles.
Dodecagon: a regular polygon with 12 equal sides and 12 same angles
Triskaidecagon: Has 13 equal sides and 13 same angles.
Tetrakaidecagon: Has 14 equal sides and 14 same angles.
Pentadecagon: A pentadecagon is a regular polygon with 15 equal sides and 15 same angles.
Hexakaidecagon: has 16 sides and angles.
Heptadecagon: Has 17 sides and angles.
Octakaidecagon: Has 18 sides and angles
Enneadecagon: 19 sides and 19 angles.
Icosagon: Has equal sides and 20 equal angles
Hectagon: Has 100 equal sides and 100 equal angles.
Chiliagon: Has 1000 sides
Myriagon: 10000 sides.
Megagon: One million sides.
n-gon: Has n- equal sides.

Irregular polygon

An irregular polygon is a polygon with a different measure of angles and side lengths.

Examples of irregular polygons:

Convex Polygon

This is a type of polygon with all the interior angles strictly less than 180 degrees. The vertex of a convex polygon always points outwards from the center of the shape.

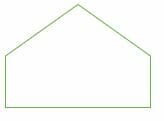
Concave Polygon

If one or more interior angles of a polygon are more than 180 degrees, it is known as a concave polygon. A concave polygon can have at least four sides—the vertex points towards the inside of the polygon.

The following are a few mnemonics to help remember the names of some polygons:

A QuadBike has 4 wheels and thus a quadrilateral.
The Washington DC in the US has 5 sides (Pentagon).
A Honeycomb has 6 sides (Hexagon).
Septagon has 7 sides (Seven).
An Octopus has 8 tentacles (octagon).
The terms Nonagon and Nine both start with the letter N.
A Decagon has 10 sides, just like a Decimal point has 10 digits.

Real-life applications of polygons

Understanding shapes is important in geometry. Shapes have a wide application in real-life applications.

For example:

The tiles that you walk on are squared in shape, which implies that they are polygons.
The truss of a building or bridge, the walls of a building, etc., are examples of polygons. Trusses are triangular in shape, while walls are rectangular shaped.
The rectangular part of a chair on which you are sitting is an example of a polygon.
The rectangular-shaped screen of your laptop, television, or mobile phone is an example of a polygon.
A rectangular football pitch or playground is an example of a polygon.
The Bermuda Triangle, which is a triangular shape, is a polygon.
The Pyramids of Egypt are also an example of polygons (triangular)
Star-shaped figures are examples of a polygon.
Road signs are also an example of polygons.

Example

John has a rectangular piece of paper. He wants to cut the paper so that he gets two more polygons (other than a rectangle) of the same size and shape. Suggest the possible ways.

Solution

There are two possible ways to cut a rectangular piece of paper in such a way that he gets two more polygons (other than a rectangle) of the same size and shape:

He can cut a rectangular piece of paper exactly from the center vertically to get the two squares of the same size and shape.
He can cut a rectangular piece of paper diagonally to get the two triangles of the same size and shape.