Proportions – Explanation & Examples

It is difficult to imagine how our life would be without mathematical concepts such as proportions. In our day to day life, we frequently encounter proportions and ratios when going for shopping, cooking and when on a vocational trip etc.

Ratios and proportions are essential for – effective performance. In this, article we shall learn how to calculate proportions and apply the knowledge to solve sample problems, but before that, let’s begin by defining ratios.

A ratio is a way of making comparisons between two or more quantities. The sign used to denote a ratio is colon ‘:’ Suppose a and b are two different quantities or numbers, then the ratio of a to b can be written as as a/b or a: b. Similarly, the ratio of b to a can also be represented as b: a or b/a. The first quantity in a ratio is known as antecedent and the second value is referred to as the consequent.

Examples of ratios are: ¾ or 3: 4, 1/5 or 1: 5, 199/389 or 199:389 etc. It is evident from this example that, a ratio is simply a fraction where the antecedent is the numerator and the consequent is the denominator.

The famous Vitruvian Man drawing of Leonardo da Vinci was based on the ideal ratio of the human body. Each part of the body takes up different ratio, like face takes up about 1/10 of the total height, and head takes up about 1/8 of the total height. The writers in middle ages used the word proportio (proportion) for the first time. In 1948, Le Corbusier gave a system of proportions

What is a Proportion?

A proportion is an expression which tells us that, two ratios are equivalent. Two ratios are said to be in proportional if they are equivalent. Proportions are represented by the by the sign ‘:’ or ‘=’. For instance, if a, b, c and d are integers, then the proportion is written as a: b = c: d or a/b = c/d or b: a = d: c.  For example, the ratios 3: 5 and 15: 25 are proportional and are written as 3: 5= 15: 25

The four numbers a, b, c and d are known as the terms of a proportion. The first a and the last term d are referred to as extreme terms while the second and third terms in a proportional are called mean terms.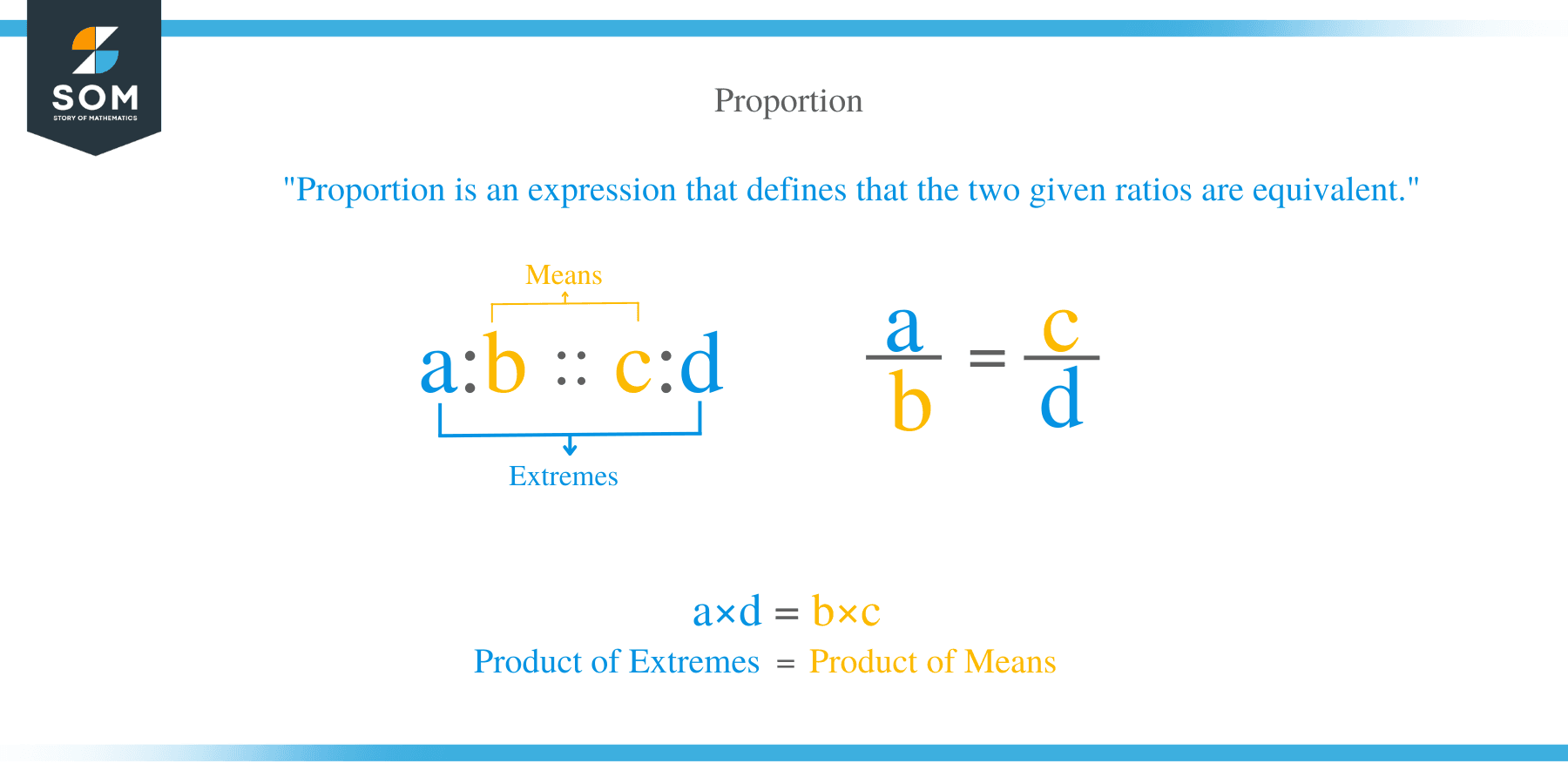

How to Solve Proportions?

It is easy to calculate if ratios are proportional. To check if the ratio a: b and c: d is proportional.

• Multiply the first term with the last term: a x d
• Multiply the second term with the third term: b x c
• If the product of extreme terms is equal to the product of mean terms, then the ratios are proportional: a x d = b x c

Continued proportion

Two ratios a: b and b: c is said to be in continued proportion if a: b = b: c. In this case, the term c is called the third proportion of a and b whereas b is called the mean proportion of between the terms a and c.

When the terms a, b and c are in continued proportion, the following formula is derived:

a/b = b/c

Cross multiplying the terms gives; a x c =b x b, Therefore,

b² = ac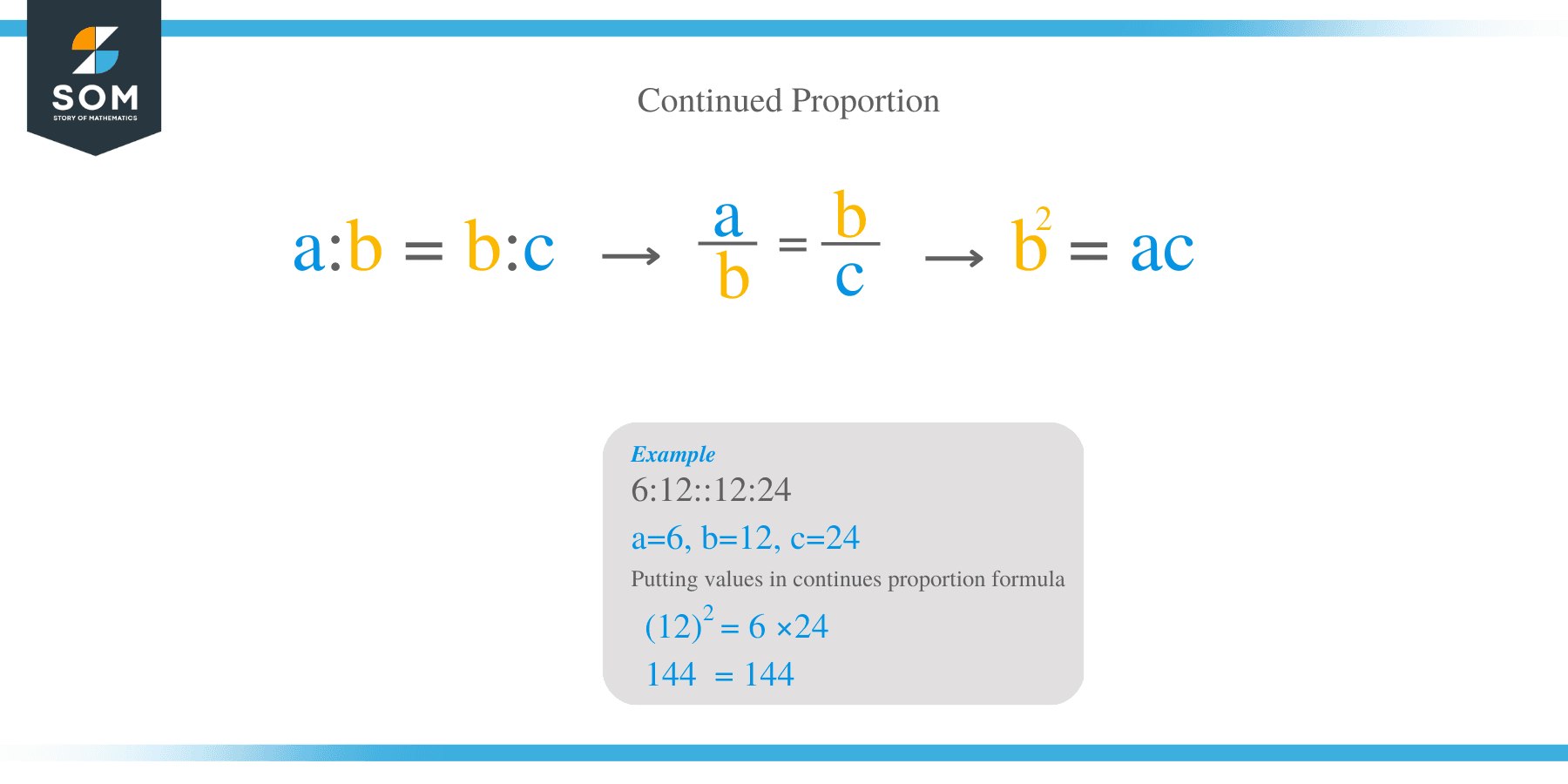

Example 1

Find out if the following ratios are in proportion: 8:10 and 12:15.

Explanation

• Multiply the first and fourth terms of the ratios.

8 × 15 = 120

• Now multiply the second and third term.

10 × 12 = 120

• Since the product of the extremes is equal to the product of the means,
• Since, the product of means (120) = product of extremes (120),
• Therefore, 8: 10 and 12:15 are proportional.

Example 2

Verify if the ratio 6:12::12:24 is proportion.

Explanation

• This is a case of continued proportion, therefore apply the formula a x c =b x b,
• In this case, a: b:c =6:12:24, therefore a=6, b=12 and c=24
• Multiply the first and third terms:

6 × 24 = 144

• Square of the middle terms:

(12) ² = 12 × 12 = 144

• Therefore, the ratio 6:12:24 is in proportion.

Example 3

If 12:18::20: p. Find the value of x to make the ratios proportional?

Explanation

Given: 12: 18::20: p

Equate the product of extremes to the product of means;
⇒ 12 × p = 20 × 18
⇒ p = (20 × 18)/12

Solve for p;
⇒ p = 30
Hence, the value of p= 30

Example 4

Find the third proportional to 3 and 6.

Explanation

• Let the third proportional be c.
• Then, b² = ac
  6 x 6 = 3 x c

C= 36/3

= 12

Thus, the third proportional to 3 and 6 is 12

Example 5

Calculate mean proportional between 3 and 27

Explanation

• Let the mean proportional between 3 and 27 be m.
• By applying the formula b² = ac; ‘

Therefore, m x m = 27 x 3 = 81

m² =81
⇒ m = √81
⇒ m = 9
Hence, the mean proportional between 3 and 27 is 9

Example 6

Given the ratios a: b = 4 :5 and b:c = 6 :7, Determine the ratio a: b: c.

Explanation

• Since b is the common term between the two ratios;
• Multiply each term in the first ratio by the value of b in the second ratio;

a:  b = 4: 5 = 24:30,

• Also multiply each term in the second ratio by the value of b in the first ratio;

b: c = 6: 7 = 30: 35

Therefore, the ratio a: b: c = 24:30:35

Golden Ratio

The biggest application of the proportion is the golden ratio, which helped a lot in analyzing proportions of different objects and man-made systems like financial markets. The two quantities are said to be in golden ratio if their ratio is equal to the ratio of their sum to the larger of the two quantities i.e. (a + b)/a = a/b, where a > b > 0.

This ratio is represented by a Greek letter φ. Further simplifying this equation, we get, φ ² – φ – 1 = 0. And solving this using a quadratic formula, we get φ = 1.6180339887…

Euclid and many mathematicians after him worked on the golden ratio and found its existence in the regular pentagon and golden rectangle.