Quadrilaterals – Explanation & Examples

Different types of shapes differ from each other in terms of sides or angles. Many shapes have 4 sides, but the difference in angles on their sides makes them unique. We call these 4-sided shapes the quadrilaterals.

In this article, you will learn:

• What a quadrilateral is.
• How the different types of quadrilaterals look like.
• The properties of quadrilaterals.

What is a Quadrilateral?

As the word suggests, ‘Quad’ means four and ‘lateral’ means side. Therefore a quadrilateral is a closed two-dimensional polygon made up of 4-line segments. In simple words, a quadrilateral is a shape with four sides.

Quadrilaterals are everywhere! From the books, chart papers, computer keys, television, and mobile screens. The list of real-world examples of quadrilaterals is endless.

Types of Quadrilaterals

There are six quadrilaterals in geometry. Some of the quadrilaterals are surely familiar to you, while others may not be so familiar.

Let’s take a look.

• Rectangle
• Squares
• Trapezium
• Parallelogram
• Rhombus
• Kite

 A rectangle

A rectangle is a quadrilateral with 4 right angles (90°). In a rectangle, both the pairs of opposite sides are parallel and equal in length.

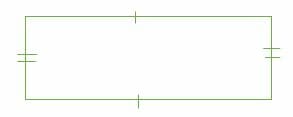
Properties of rectangles:

• All angles are right angles.
• The diagonals are congruent.

Rectangles are very handy to have around. For example, shoe boxes, chopping boards, sheets of paper, picture frames, etc., are rectangular in shape.

Rectangles are easy to stack because they have two pairs of parallel sides. Their right angles make sure built things such as houses, office buildings, schools, etc., stand straight and tall.

A square

A square is a quadrilateral with 4 right angles (90°). In a square, both pairs of opposite sides are parallel and equal in length.

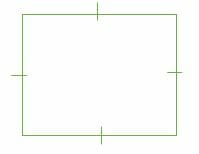
Properties of a square:

• All sides of a square are congruent.
• All angles are right angles by definition.

Real-life examples of squares include computers, keys, coasters, spaces on a chessboard, etc.

Parallelogram

A parallelogram is a quadrilateral with 2 pairs of parallel opposite and equal sides. Similarly, the opposite angles in a parallelogram are equal in measure.

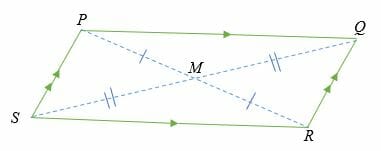
In the parallelogram PQRS, side PQ is parallel to side SR, and side PS is parallel to side QR. Point M is the midpoint of the two diagonals of the parallelogram.

Therefore, length PM = MR, & length SM = MQ

Rhombus

A rhombus is a quadrilateral with all four sides having equal lengths. The Opposite sides of a rhombus are equal and parallel, and the opposite angles are the same.

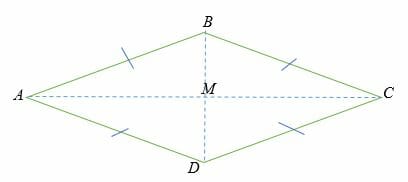
ABCD is a rhombus in which AB is parallel and equal to DC and AD is also parallel and equal to BC.

The diagonals AC = BD, and M is the point of intersection of the two diagonals.

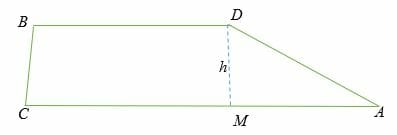
Trapezium

A trapezium or a trapezoid is an equilateral with one pair of opposite parallel sides. The sides of a trapezium are known as bases, and the perpendicular line from any vertex of the trapezium to the base is known as the height.

ABCD is a trapezium in which side BD is parallel to side CA. The perpendicular line DM is the height (h) of the trapezium, while BD and CA are the bases.

Kite

A kite is a quadrilateral with two pairs of side lengths, and these sides are adjacent to each other.

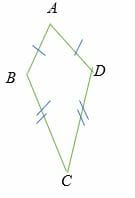
Properties of a rhombus

• All sides are congruent by definition.
• The diagonals bisect the angles.
• The diagonals in a kite bisect each other at right angles.

Properties of Quadrilaterals

The properties of quadrilaterals include:

• Every quadrilateral has 4 sides, 4 vertices, and 4 angles.4
• The total measure of all the four interior angles of a quadrilateral is always equal to 360 degrees.
• The sum of interior angles of a quadrilateral fits the formula of polygon i.e.

Sum of interior angles = 180 ° * (n – 2), where n is equal to the number of sides of the polygon

• Rectangles, rhombus, and squares are all types of parallelograms.
• A square is both a rhombus and a rectangle.
• The rectangle and rhombus are not square.
• A parallelogram is a trapezium.
• A trapezium is not a parallelogram.
• Kite is not a parallelogram.

Classification of quadrilaterals

The quadrilaterals are classified into two basic types:

• Convex quadrilaterals: These are the quadrilaterals with interior angles less than 180 degrees, and the two diagonals are inside the quadrilaterals. They include trapezium, parallelogram, rhombus, rectangle, square, kite, etc.
• Concave quadrilaterals: These are the quadrilaterals with at least one interior angle greater than 180 degrees, and at least one of the two diagonals is outside the quadrilaterals. A dart is a concave quadrilateral.

There is another less common type of quadrilaterals, called complex quadrilaterals. These are crossed figures. For example, crossed trapezoid, crossed rectangle, crossed square, etc.

Let’s work on a few example problems about quadrilaterals.

Example 1

The interior angles of an irregular quadrilateral are; x°, 80°, 2x°, and 70°. Calculate the value of x.

Solution

By a property of quadrilaterals (Sum of interior angles = 360°), we have,

⇒ x° + 80° + 2x° + 70° =360°

Simplify.

⇒ 3x + 150° = 360°

Subtract 150° on both sides.

⇒ 3x + 150° – 150° = 360° – 150°

⇒ 3x = 210°

Divide both sides by 3 to get;

⇒ x = 70°

Therefore, the value of x is 70°

And the angles of the quadrilaterals are; 70°, 80°, 140°, and 70°.

Example 2

The interior angles of a quadrilateral are; 82°, (25x – 2) °, (20x – 1) ° and (25x + 1) °. Find the angles of the quadrilateral.

Solution

The total sum of interior angles of in a quadrilateral = 360°

⇒ 82° + (25x – 2) ° + (20x – 1) ° + (25x + 1) ° = 360°

⇒ 82 + 25x – 2 + 20x – 1 + 25x + 1 = 360

Simplify.

⇒ 70x + 80 = 360

Subtract both sides by 80 to get;

⇒ 70x = 280

Divide both sides by 70.

⇒ x = 4

By substitution,

⇒ (25x – 2) = 98°

⇒ (20x – 1) = 79°

⇒ (25x + 1) = 101°

Therefore, the angles of the quadrilateral are; 82°, 98°, 79°, and 101°.