Radicals that have Fractions – Simplification Techniques

A radical can be defined as a symbol that indicates the root of a number. Square root, cube root, fourth root are all radicals. This article introduces by defining common terms in fractional radicals. If n is a positive integer greater than 1 and a is a real number, then;

ⁿ√a = a ^1/n,

where n is referred to as the index and a is the radicand, then the symbol √ is called the radical. The right and left side of this expression is called exponent and radical form respectively.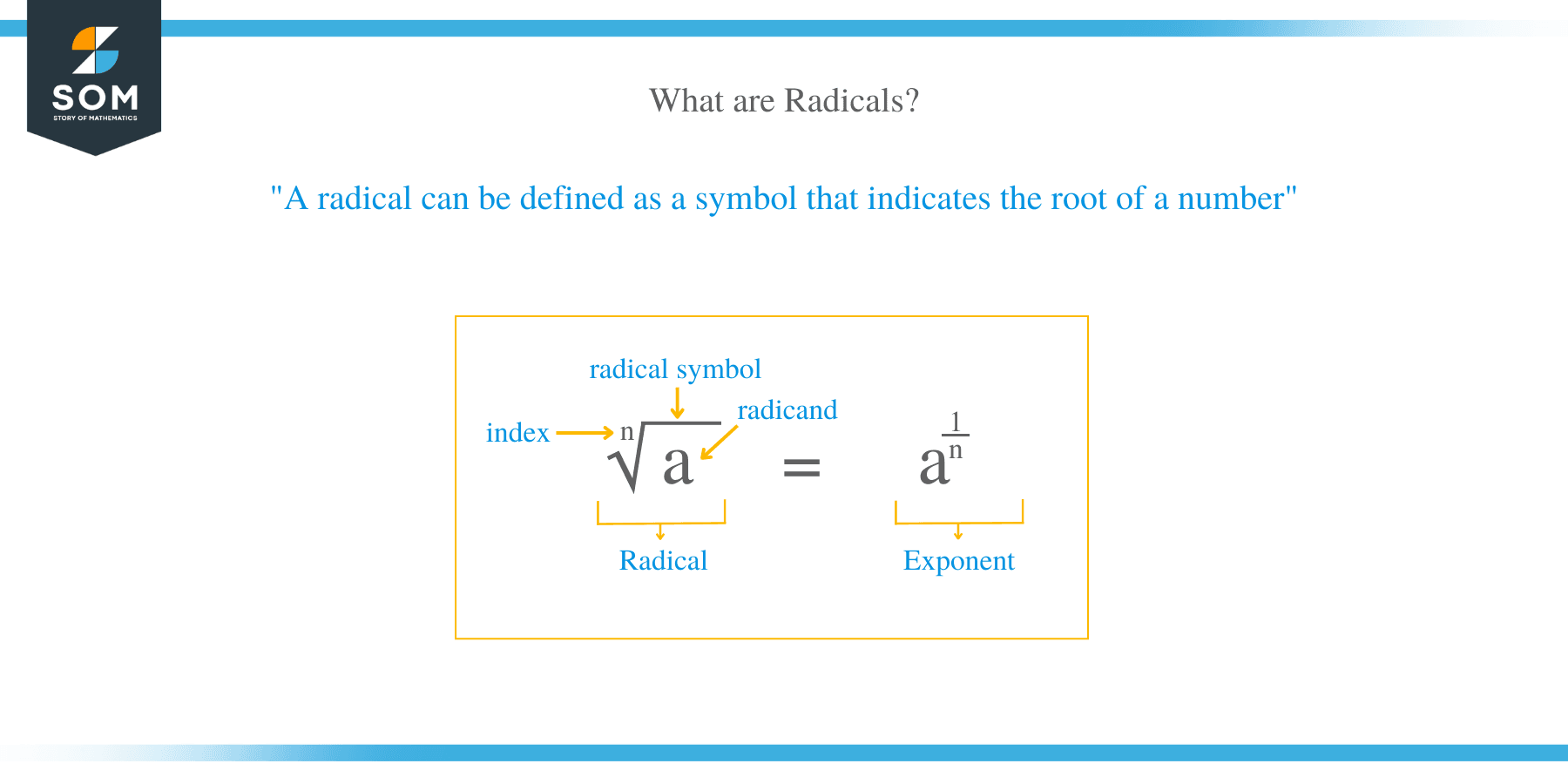

How to Simplify Fractions with Radicals?

• Simplifying a radical by factoring out.
• Rationalizing the fraction or eliminating the radical from the denominator.

Simplifying Radicals by Factoring

Let’s explain this technique with the help of the example below.

Example 1

Simplify the following expression:

√27/2 x √(1/108)

Solution

Two radical fractions can be combined by following these relationships:

√a / √b = √(a / b)  and √a x √b =√ab

Therefore,

√27/2 x √(1/108)

= √27/√4 x √(1/108)

= √(27 / 4) x √(1/108)

= √(27 / 4) x √(1/108) = √(27 / 4 x 1/108)

= √(27 / 4 x 108)

Since 108 = 9 x 12 and 27 = 3 x 9

√(3 x 9/ 4 x 9 x 12)

9 is a factor of 9, and so simplify,

√(3 / 4 x 12)

= √(3 / 4 x 3 x 4)

= √(1 / 4 x 4)

=√(1 / 4 x 4) = 1 / 4

Simplifying Radicals by Rationalizing the Denominator

Rationalizing a denominator can be termed an operation where the root of an expression is moved from the bottom of a fraction to the top. The bottom and top of a fraction are called the denominator and numerator, respectively. Numbers such as 2 and 3 are rational, and roots such as √2 and √3 are irrational. In other words, a denominator should always be rational, and this process of changing a denominator from irrational to rational is what is termed as “Rationalizing the Denominator.”

There are two ways of rationalizing a denominator. A radical fraction can be rationalized by multiplying both the top and bottom by a root:

Example 2

Rationalize the following radical fraction: 1 / √2

Solution

Multiply both the numerator and denominator by the root of 2.

= (1 / √2 x √2 / √2)

= √2 / 2

Another method of rationalizing the denominator is the multiplication of both the top and bottom by a conjugate of the denominator. A conjugate is an expression with a changed sign between the terms. For example, a conjugate of an expression such as x ² + 2 is

x ² – 2.

Example 3

Rationalize the expression:1 / (3 − √2)

Solution

Multiply both the top and bottom by the (3 + √2) as the conjugate.

1 / (3 − √2) x (3 + √2) / (3 + √2)

= (3 + √2) / (3 ² – (√2) ²)

= (3 + √2) / 7, the denominator is now rational.

Example 4

Rationalize the denominator of the expression; (2 + √3)/(2 – √3)

Solution

• In this case, 2 – √3 is the denominator and rationalizes the denominator, both top and bottom by its conjugate.

The conjugate of 2 – √3 = 2 + √3.

• Comparing the numerator (2 + √3) ² with the identity (a + b) ²= a ²+ 2ab + b ², the result is 2 ² + 2(2)√3 + √3² =  (7 + 4√3)
• Comparing the denominator with the identity (a + b) (a – b) = a ² – b ², the results is 2² – √3²

Example 5

Rationalize the denominator of the following expression,

(5 + 4√3)/(4 + 5√3)

Solution

• 4 + 5√3 is our denominator, and so to rationalize the denominator, multiply the fraction by its conjugate; 4+5√3 is 4 – 5√3
• Multiplying the terms of the numerator; (5 + 4√3) (4 – 5√3) gives out 40 + 9√3
• Compare the numerator (2 + √3) ² the identity (a + b) ²= a ²+ 2ab + b ², to get

4 ²- (5√3) ² = -59

Example 6

Rationalize the denominator of (1 + 2√3)/(2 – √3)

Solution

• We have 2 – √3 in the denominator, and to rationalize the denominator, multiply the entire fraction by its conjugate

Conjugate of 2 – √3 is 2 + √3

• We have (1 + 2√3) (2 + √3) in the numerator. Multiply these terms to get, 2 + 6 + 5√3
• Compare the denominator (2 + √3) (2 – √3) with the identity

a ²- b ² = (a + b) (a – b), to get 2 ² – √3 ² = 1

Example 7

Rationalize the denominator,

(3 + √5)/(3 – √5) + (3 – √5)/(3 + √5)

Solution

• Find the LCM to get (3 +√5)² + (3-√5)²/(3+√5)(3-√5)
• Expand (3 + √5) ² as 3 ² + 2(3)(√5) + √5 ² and  (3 – √5) ² as 3 ²- 2(3)(√5) + √5 ²

Compare the denominator (3-√5)(3+√5) with identity a ² – b ²= (a + b)(a – b), to get

3 ² – √5 ² = 4

Example 8

Rationalize the denominator of the following expression:

[(√5 – √7)/(√5 + √7)] – [(√5 + √7) / (√5 – √7)]

Solution

• By calculating the L.C.M, we get

(√5 – √7) ² – (√5 + √7) ² / (√5 + √7)(√5 – √7)

• Expansion of (√5 – √7) ²

= √5 ² + 2(√5)(√7) + √7²

• Expansion of (√5 + √7) ²

= √5 ² – 2(√5)(√7) + √7 ²

• Compare the denominator (√5 + √7)(√5 – √7) with the identity

a² – b ² = (a + b)(a – b), to get

√5 ² – √7 ² = -2